事实上，以上已讨论了制定电力网络等值电路的全过程。制定电力网络等值电路的方法分两大类：有名制——所有参数和变量都以有名单位，如Ω、S、kV、kA、MVA等表示；图2-10以标么制表示的电力网络等值电路标么制——所有参数和变量都以与它们同名基准值相对的标么值表示，因此都没有单位。......
2023-06-15
电力线路的等值电路理论与应用
【摘要】：当x＝0时，和由式和式可得由此可以解出将A1和A2代入式和式便得上式可利用双曲线函数写成当x＝l时，可得到线路首端电压和电流与线路末端电压和电流的关系如下将上述方程同二端口网络的通用方程相比较，若取和输电线就是对称的无源二端口网络，并可用对称的等值电路来表示。由于复数双曲线函数的计算很不方便，需要做一些简化。
1.电力线路的方程式
设有长度为l的电力线路，其参数沿线均匀分布，单位长度的阻抗和导纳分别为z1＝r1＋jx1，y1＝g1＋jb1。在距末端x处取一微段dx，可做出等值电路如图2-1所示。在正弦电压作用下处于稳态时，电流I.在dx微段阻抗中的电压降为
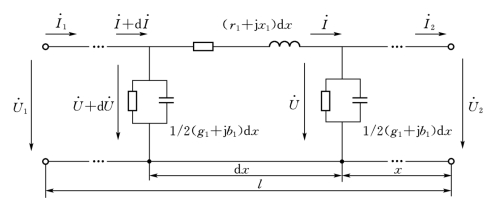
图2-1 长线的等值电路
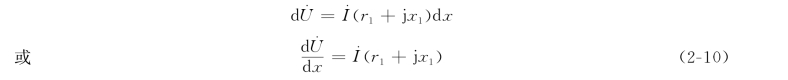
流入dx微段并联导纳中的电流为
略去二阶微小量，便得
将式（2-10）对x求导数，计及式（2-11），便得
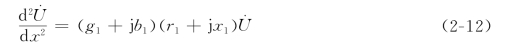
上式为二阶常系数齐次微分方程式，其通解为
将式（2-13）代入式（2-10），便得
上两式中 γ——线路的传播常数；
Zc——线路的物理阻抗。
它们的大小由下式确定
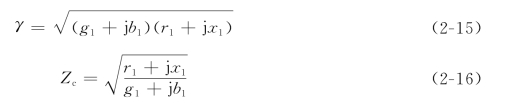
长线方程稳态解式（2-13）和式（2-14）中的积分常数A1和A2可由线路的边界条件确定。当x＝0时，
和
由式（2-13）和式（2-14）可得
由此可以解出
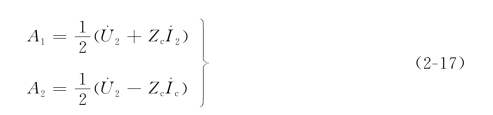
将A1和A2代入式（2-13）和式（2-14）便得
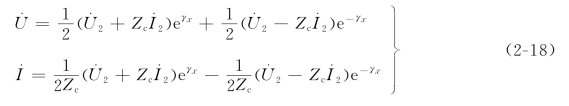
上式可利用双曲线函数写成
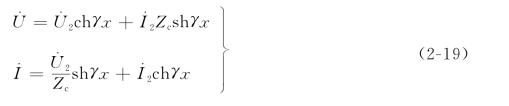
当x＝l时，可得到线路首端电压和电流与线路末端电压和电流的关系如下
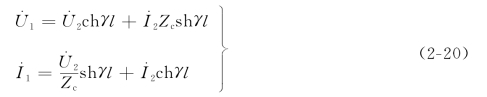
将上述方程同二端口网络的通用方程
相比较，若取
和
输电线就是对称的无源二端口网络，并可用对称的等值电路来表示。
2.输电线的集中参数等值电路
方程式（2-20）表明了线路两端电压和电流的关系，它是制订集中参数等值电路的依据。图2-2中的Π型和T型电路均可作为输电线的等值电路，Π型电路的参数为
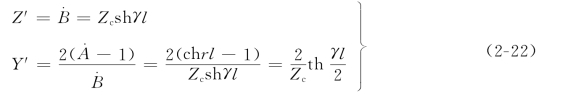
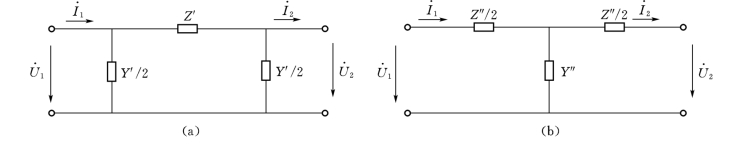
图2-2 长线的集中参数等值电路
T型电路的参数为
实际计算中大多采用Π型电路代表输电线，现在对Π型电路的参数计算作进一步的讨论。由于复数双曲线函数的计算很不方便，需要做一些简化。
令Z＝（r1＋jx1）l和Y＝（g1＋jb1）l分别代表全线的总阻抗和总导纳，将式（2-22）改写为
式中
由此可见，将全线的总阻抗Z和总导纳Y分别乘以修正系数KZ和KY，便可求得Π型等值电路的精确参数。
利用双曲线函数的幂级数展式
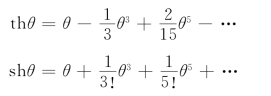
将式（2-25）的右端展开，并取其前两项，便得
如果略去输电线的电导，再利用修正系数的简化公式（2-26），便可得到
其中
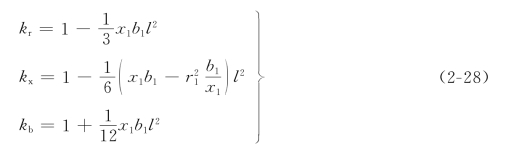
在计算Π型等值电路的参数时，可以将一段线路的总阻抗和总导纳作为参数的近似值，也可以按公式（2-27）对近似参数进行修正，或者用公式（2-22）计算其精确值。
在工程计算中，既要保证必要的精度，又要尽可能的简化计算，采用近似参数时，长度不超过300km的线路可用一个Π型电路来代替，对于更长的线路，则可用串级联接的多个Π型电路来模拟，每一个Π型电路代替长度为200～300km的一段线路。采用修正参数时，一个Π型电路可用来代替500～600km长的线路。还须指出，这里所讲的处理方法仅适用于工频下的稳态计算。
有关电力系统分析的文章
- 详细阅读
-
变压器Π型等值电路的原理与应用详细阅读
为此，可以在变压器等值电路中增添只反映变比的理想变压器。双绕组变压器的这种等值电路示于图2-4中。变压器的Π型等值电路中三个阻抗（导纳）都与变比k有关，Π型的两个并联支路的阻抗（导纳）的符号总是相反的。与双绕组变压器一样，可以做出电气上直接相连的三绕组变压器等值电路，如图2-6所示。图2-6三绕组变压器的等值电路变压器采用Π型等值电路后，电力系统中与变压器相接的各元件就可以直接应用其参数的实际值。......
2023-06-15
-
电力制动线路的使用与维护详细阅读
电力制动是在切断电动机电源后，利用电气线路让电动机产生与旋转方向相反的制动转矩进行制动。电力制动方式主要有反接制动、能耗制动和电容制动等。图3-67 双向起动反接制动控制线路3）正向全速运行控制。图3-68 无变压器单相半波整流能耗制动控制线路5）断开电源开关QS。图3-70 电容制动控制线路线路工作原理分析如下：1）闭合电源开关QS。......
2023-06-15
-
电力拖动线路设计探析详细阅读
选配接触器时，可根据电力拖动线路的电源类型进行选择。如图6-56所示，电力拖动线路中常用的继电器主要有电磁继电器、固态继电器、时间继电器、中间继电器、温度继电器、过热保护继电器、速度继电器、压力继电器、电流继电器、电压继电器等。......
2023-06-24
-
架空电力线路标准与规范汇总详细阅读
1.GB50173—02《35kV及以下架空电力线路施工及验收规范》2.GB50061—2010《66kV及以下架空电力线路设计规范》3.GB50233—2005《110kV—500kV架空电力线路施工及验收规范》4.GB50173—928《电气装置安装工程35kV及以下架空电力线路施工及验收规范》5.GB50168—92《电气装置安装工程电缆线路施工及验收规范》6.GB50194—2014《建设......
2023-06-15
-
电力拖动线路的安装和调试详细阅读
图解演示电力拖动线路设计及主要部件选配完成后，即可根据所设计的电力拖动线路，对其主要部件进行安装接线操作，并对安装完毕后的线路进行调试。下面我们以电动机连续控制线路为例对其安装与调试进行介绍。电力拖动线路的通电测试通电测试电力拖动线路时，应严格按照安全操作规程中的有关规定进行实际操作，以确保人身安全。......
2023-06-24
-
电力线路中的电压降低与损耗问题详细阅读
在计算线路电压中，常用到电压降落、电压损耗、电压偏移、电压调整等几个指标，它们的定义如下：电压降落。指线路始末两端电压的向量差它的两个分量ΔU.和δU.分别称为电压降落的纵分量和横分量。电压偏移也常以线路额定电压UN百分数表示，即电压调整。由于输电线路的电容效应，特别是超高压线路，在空载时线路末端电压上升较大。......
2023-06-15
-
变压器零序连接的等值电路和外电路详细阅读
变压器的零序等值电路与外电路的连接，取决于零序电流的流通路径，因而与变压器三相绕组连接形式及中性点是否接地有关。当外电路向变压器某侧三相绕组施加零序电压时，如果能在该侧绕组产生零序电流，则等值电路中该侧绕组端点与外电路接通；如果不能产生零序电流，则从电路等值的观点，可以认为变压器该侧绕组与外电路断开。......
2023-06-15
相关推荐