如何使用计时/计转数定距空炸弹药？

2023-06-15 历史故事版权反馈

【摘要】：传统计时定距空炸引信仅装定时间, 但计时工具误差较大, 且不能基于弹丸初速自修正飞行时间, 弹丸定距空炸精度较差。目前实现计转数的理论方法有多种, 常见的有章动法、地磁法、离心法等。由于章动和进动的存在, 引信转轴的瞬时轴线与弹丸惯性主轴呈一夹角。

1.计时定距空炸弹药

计时定距空炸方法不限于弹种, 可适用于线膛炮发射的滚转稳定榴弹, 也可适用于滑膛炮发射的弹丸, 同时也可适用于迫击炮弹及火箭弹等。传统计时定距空炸引信仅装定时间, 但计时工具误差较大, 且不能基于弹丸初速自修正飞行时间, 弹丸定距空炸精度较差。随着硬件基础的提高, 21 世纪初国内学者开始研究基于初速修正的计时定距空炸方法, 在理论上提出了诸多基于初速修正的计时方法, 射击试验也表明, 基于初速修正的计时定距方法比单纯计时定距方法精度成倍提高。

1) 初速测量原理

本书提到的初速修正是指弹丸发射后自测初速, 根据初速计算飞行时间,其原理是: 弹丸发射后, 引信组件测量出弹丸滚转速度, 再利用弹体转速计算出弹丸初速。

旋转稳定弹使用线膛火炮发射, 火炮身管内有若干条膛线, 每条膛线都呈螺旋状从药室向炮口延伸, 膛线的凸起部为阳线, 凹槽部分为阴线。发射时,弹带在火药气体的压力作用下被迫挤进膛线凹槽内, 使弹丸在沿身管轴线前进的过程中也沿膛线旋转, 形成炮口转速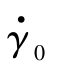 pagenumber_ebook=186,pagenumber_book=170 。膛线沿膛壁旋转一周前进的距离称为膛线导程h 。在弹丸刚出炮口时, 弹丸初始滚转速率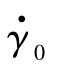与初速V0 关系可用如下公式表示:

弹丸出炮口时初始滚转一圈时间τ0 与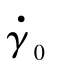 pagenumber_ebook=186,pagenumber_book=170 的关系为

由式(5 -1) 和式(5 -2) 得

即在弹丸刚出炮口阶段, V0 与τ0 是一一对应的, 且两者成反比关系。

在实际应用中可利用τ0 与V0 的关系进行弹丸测速, 进而计算预定射距上的飞行时间, 而τ0 的获取将在本章后面讲解。

2) 计时计算方法

(1) 反比例修正法。

有学者指出, 当射距一定时, 弹丸飞行时间t 与V0 成反比关系, 则t 与τ0呈线性关系, 设

式中, N 为直线斜率。则在实际应用中, 根据V0 及射距可通过弹道模型计算弹丸飞行时间t, 再由式(5 -4) 计算出N。将N 装定给定距空炸弹丸引信,弹丸发射后其实际滚转一圈时间为τ01 , 则弹丸定距空炸时间为

τ01 中包含了弹丸速度信息, 式 (5 -5) 是常用基于弹丸初速修正的计时定距空炸理论方法。

(2) 平均速度修正法。

平均速度修正法是根据弹丸的射程随时间几乎呈线性变化, 近似认为弹丸的平均速度与时间的乘积等于射程。根据射程相等原则, 利用弹丸的飞行时间与平均速度的倒数成正比进行修正, 修正公式为

式中, x 为预定射距;t0 为利用弹道模型计算出的弹丸飞行到预定射距上的理论飞行时间; v0 为火炮自身最新状态下的平均初速, 上述三个值均需在射击前通过装定器装定给弹丸引信; v′ 为弹丸引信测得的初速。

(3) 一次函数修正法。

一次函数修正法是根据弹丸的飞行时间改变量与弹丸的速度改变量呈线性关系, 即在理论飞行时间的基础上加上时间修正项, 修正公式为

2.计转数定距空炸弹药

计转数定距空炸原理及实现方法相对于基于初速修正的计时定距空炸方法简单, 该方法多适用于线膛火炮发射的滚转榴弹, 通过在全弹道建立弹丸总滚转圈数与飞行距离的关系, 即可根据射击距离装定对应弹丸滚转圈数,弹丸发射后计算弹丸滚转圈数, 当达到装定值时引爆弹丸, 起到定距空炸的目的。

计转数引信是一种以微电子技术为基础、以弹丸的自转周期为计数脉冲,并对影响因素进行修正, 达到较高炸点精度的机电引信。而计转数引信的关键技术是一个小型化、抗高过载的计转数技术和电源快速供电技术。目前实现计转数的理论方法有多种, 常见的有章动法、地磁法、离心法等。

1) 章动计转数法

根据旋转弹外弹道理论可知:

进动角方程为

章动角方程为

式中, δm 为最大章动角,为起始章动角角速度; σ 为稳定参数(0 ＜σ ＜1);α 为进动角速度,α = Cr0/(2A) ;C 为赤道转动惯量;A 为极转动惯量; r0 为自转角速度。

自转角:

弹丸瞬时角速度:

式中, i′、j′、k′为弹丸惯性主轴坐标系 (弹体坐标系) 单位坐标; p、q、r 为ω 在弹丸惯性主轴坐标系的分量, ω2 = p2 + q2 + r2 , 且

弹丸瞬时角加速度:

写成分量形式为

式中, εx′ 、εy′ 、εz′ 为ε 在弹丸惯性主轴坐标系的分量。

绕心运动质点的加速度对弹丸上的固定质点(x′,y′,z′) , 忽略质心运动的绝对加速度时, 绕心运动的加速度为

写成分量形式为

式中, ax′ 、ay′ 、az′ 为a 在弹丸惯性主轴坐标系的分量。

由于章动和进动的存在, 引信转轴的瞬时轴线与弹丸惯性主轴呈一夹角。同时, 自转角速度大于章动和进动角速度, 所以弹丸上一点的偏心距也随着自转而变化, 绕心加速度信号的周期与自转相关, 即与导程相关, 而与初速基本无关。因此, 它可以提供准确的距离信息, 利用转数与距离的关系实现定距起爆。弹丸绕心运动满足的方程:

根据绕心运动理论, 切向加速度信号可作为计算导程数的脉冲信号, 检测其交流分量的峰值还可测得最大章动角, 检测信号周期可测得弹丸炮口速度,进一步修正, 可提高炸点精度。因此, 计转数引信利用绕心运动加速度信号实现定距起爆的方案具有理论可行性。但目前未见有该理论应用于实际。

2) 地磁计转数法

当闭合线圈平面法线与地磁线成一角度φ , 并以ω 绕平面轴线旋转时, 在线圈内将产生感应电动势ε

设地磁场强度为B, 线圈匝数为n, 线圈平面为S, 则

从式(5 -19) 可看出, 弹丸转动一圈正好对应地磁线圈感应电动势的正弦波的一个周期。

3) 离心计转数法

采用半导体压电应变阀敏感应力测出离心力, 通过离心力求出旋转角速度ω , 再由ω 得出转数n, 其数学模型如下:

当引弹系统旋转时, 其敏感体所受的离心力为

式中, m 为敏感体质量; R 为敏感体到旋转轴心的距离; ω 为引弹系统旋转角速度。

由于ω = 2πf, 所以

式中, f 为引弹系统旋转频率; n 为引弹系统转动圈数; t 为弹丸飞行时间。则

即