执行机构控制技术优化方案

1.脉冲推冲器控制技术

脉冲推冲器的修正参数使得火箭弹具备了一定的弹道修正能力, 而脉冲推冲器能否对弹道偏差进行修正取决于控制算法。脉冲推冲器激活控制需要满足几个基本条件: ①预测落点偏差值大于设定的点火阈值; ②脉冲推冲器相邻点火时间间隔要大于一定的时间; ③脉冲合力加载方位和弹道修正所需方位角度偏差在要求范围内; ④每个脉冲推冲器只能使用一次。同时满足上述四个基本条件才能激活脉冲推冲器。使用脉冲推冲器进行弹道修正之前首先要确定脉冲推冲器的启控时间、点火阈值、点火相位和点火逻辑。

1) 启控时间

脉冲推冲器启控时间为火箭弹发射后脉冲推冲器进行弹道修正的最早时间, 确定脉冲推冲器的启控时间是弹道修正控制系统需要解决的首要问题。启控时间与导引算法和脉冲推冲器的弹道修正能力等因素有关。火箭弹定位成功后便可作为弹道修正的启控时间, 但为了提高脉冲推冲器的弹道修正效能还需要研究脉冲推冲器的修正能力分布情况。

火箭弹飞行过程中, 脉冲推冲器随弹体一起低速旋转, 假设某一时刻弹体的转速为ωx , 则脉冲推冲器工作时对弹体的修正力如图4 -6 所示。

从图4 -6 可以看出, 脉冲推冲器产生的脉冲力为F , 脉冲力在准弹体坐标系上的分量分别为Fy 和Fz 。假设第i 个脉冲推冲器的点火方位角为γi , 则该脉冲推冲器的合冲量大小和方向为

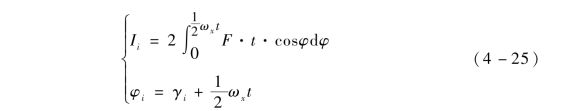
由牛顿第二定律知, 第i 个脉冲推冲器作用后在准弹体坐标系内产生的速度增量为

脉冲推冲器作用过程中弹体产生的位移变化量为

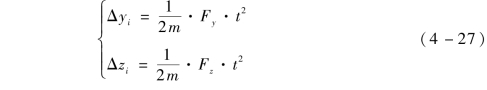
假设火箭弹主发动机关机以后质量为50 kg, 脉冲推冲器点火持续时间为23 ms, 推力为1 200 N, 由式(4 -27) 解得脉冲作用过程中弹体产生的位移极值量为厘米级, 脉冲推冲器弹道修正过程中引起的位置变量完全可以忽略不计。脉冲推冲器进行弹道修正是通过速度变化量对于时间的累积得来的。

由式(4 -26) 可得第i 个脉冲推冲器作用后弹体法向速度增量为ΔVyi ,横向速度增量为ΔVzi。

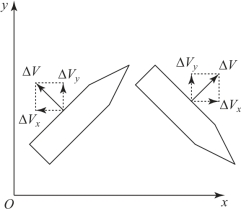
图4-7　脉冲推冲器纵向修正示意图

脉冲推冲器进行横向修正时横向修正距离取决于ΔVzi 和剩余飞行时间,ΔVzi 一定时剩余飞行时间越长横向修正距离将越大。

脉冲推冲器进行纵向修正时情况相对复杂, 脉冲推冲器进行纵向修正时速度变化如图4 -7 所示。

从图4 - 7 中可以看出, 在弹道上升段, 脉冲推冲器进行弹道修正后弹体的法向速度增加但同时减小了纵向速度。法向速度增量ΔVyi 减缓了火箭弹的落地时间, 相应地会增强纵向修正能力, 但是纵向速度减小会缩短一定时间内的飞行距离, 会减弱修正能力。在弹道的下降段, 脉冲推冲器作用后法向速度增量和纵向速度改变对于距离的修正是同方向的, 修正能力会得到加强。

为验证脉冲推冲器在不同点火方位角和不同启控时间的弹道修正效果, 选取了冲量为15 N·s、持续时间为16 ms、最大推力为1.233 kN 和推力曲线为等腰三角形的脉冲推冲器进行弹道修正仿真。假设点火方位0°角与准弹体坐标系的y4 轴重合, 从弹尾向弹头方向看, 点火方位角顺时针增大。以火箭弹质心处的脉冲推冲器作为控制对象, 在标准气象条件下, 仿真解算了以45°射角发射时脉冲推冲器在全弹道修正能力变化情况。仿真结果显示, 火箭弹在41.65 s 左右到达弹道顶点。火箭弹飞行时间-转速变化曲线如图4 -8 所示。

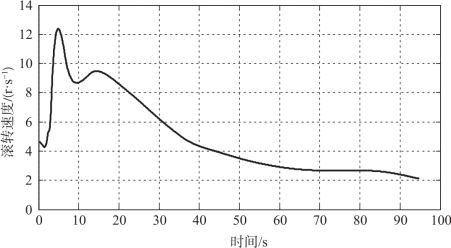
图4-8　火箭弹飞行时间-转速变化曲线

从图4 -8 可以看出, 弹体的转速范围为2 ~12.8 r/s。在弹道初始段, 弹体受到的导转力矩远大于滚转阻尼力矩, 弹体转速随着飞行时间的增加而不断增加, 发动机关机时弹体转速达到最高约12.8 r/s。发动机关机后弹体受到的滚转力矩减小, 弹体滚转速度逐渐减小, 60 s 左右导转力矩和滚转阻尼力矩达到一个平衡, 此时转速约为3 r/s。

仿真解算的单个脉冲推冲器修正能力与点火时间、点火方位的关系见表4 -3。根据表4 -3 绘制修正能力与飞行时间的对应关系, 如图4 -9 所示。

表4-3　脉冲推冲器弹道修正能力与点火时间对应关系

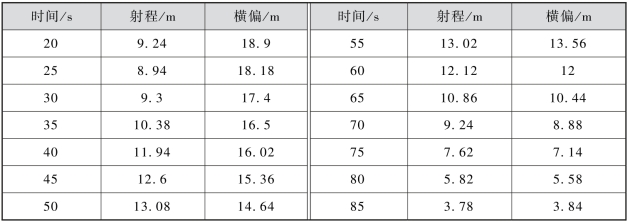
图4-9　弹道修正能力与点火时间对应关系图

从表4 -1 和图4 -9 中可以看出, 脉冲推冲器横向修正能力随着时间的推移逐渐降低, 与上面的理论分析相一致。以弹道顶点为分界点, 弹道顶点之后横向修正能力衰减的速度较弹道顶点之前快。结合图4 -8 分析可知, 火箭弹到达顶点之前, 弹体转速较高, 脉冲推冲器作用过程扫过的角度会较大, 脉冲推冲器产生的合力减小, 达到顶点以后转速小且稳定, 此时修正能力只与剩余时间有关系。

从表4 -1 和图4 -9 中还可以看出, 脉冲推冲器横向修正能力随着时间的推移而递减, 纵向修正能力在随着射程的增加而不断增强, 在弹道顶点处达到最大, 此后修正能力逐渐衰减。脉冲推冲器在上升段的横向修正能力远大于纵向修正能力, 而下降段的横向、纵向修正能力相当。

基于以上分析, 确定脉冲推冲器横向修正的启控时间为卫星数据可用时刻, 纵向修正启控时间为过弹道顶点后。

2) 点火阈值

点火阈值是指激活脉冲推冲器所需的最小落点偏差值, 点火阈值设置不合理会导致弹道偏差修正过量或者修正不足, 每一种情况都会致使火箭弹的射击精度变差, 为了提高火箭弹射击精度需要根据脉冲推冲器的弹道修正能力和弹道特点设置点火阈值。

从图4 -9 中可以看出, 不同方位、不同时刻激活脉冲推冲器对应的弹道修正能力不同。可以将脉冲推冲器的修正能力和时间的对应关系保存下来, 制成一个时间-点火阈值对应表, 见表4 -4。进行弹道修正时将预测偏差和修正能力进行比较, 如果满足预测偏差值大于对应弹道点处脉冲推冲器的弹道修正能力则激活脉冲推冲器, 此时的脉冲修正能力即为脉冲点火阈值, 由于测量误差的存在, 为避免修正过量可以在脉冲修正能力的基础上适当放大脉冲点火阈值。

表4-4　飞行时间-点火阈值对应表

从表4 -4 可以看出, 横向点火阈值随着飞行时间的增加而不断减小, 纵向点火阈值随着飞行时间的推移呈现了先增大后减小的趋势。从表4 -4 可以看出, 由于单个脉冲推冲器的修正能力很小, 理论上可以将火箭弹修正到很小的偏差范围内。

3) 点火相位

点火相位是指所需的脉冲合力与准弹体坐标轴之间的角度差。采用落点预测导引方法对脉冲推冲器进行点火控制时, 所需的脉冲修正力方位取决于射程偏差和横向偏差。

假设目标点为T , 以目标点为坐标原点在水平面内建立落点偏差坐标系,如图4 -10 所示。

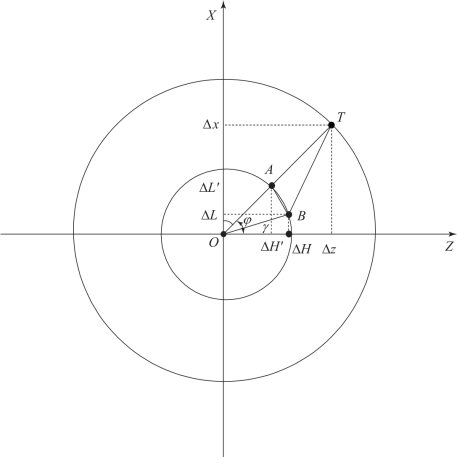
图4-10　落点偏差坐标系

从图4 -10 可以看出, O 点为目标点, OX 轴为发射点与目标点连线的延长线, 射程增加的方向为正。OZ 轴为横向偏差, 与OX 轴构成右手坐标系。OT 为预测落点偏差, Δx 为纵向预测偏差,Δz 为横向预测偏差。假设某时刻脉冲推冲器的横向、纵向修正能力分别为ΔH′和ΔL′ , 如果横向、纵向的预测偏差比值与横向、纵向修正的修正能力比值保持一致, 即

点火相位为OT 方向时剩余偏差将最小, 为AT 。但是从表4 -1 和图4 -10 中可以发现, 在同一弹道点, 脉冲力相等时横向和纵向的修正能力并不一致, 即脉冲合力方向沿OT 时对应的纵向和横向修正能力将分别为ΔL 和ΔH , 点火相位为OT 时实际剩余偏差将为BT 。由三角形的性质可知BT ＞AT , 实际剩余偏差大于最小剩余偏差。为了减小剩余误差, 需要对点火相位进行优化。相位优化的目标是确保

假设优化后的点火相位为φ , 则脉冲推冲器产生的修正力在横向和纵向分力为

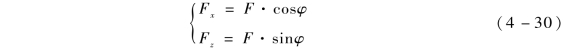
由表4 -1 可得同样的作用力在相同的时间点对于横向、纵向的修正能力不同, 假设这一比值为k, 则由式 (4 -29) 和式 (4 -30) 可得同一时间点脉冲推冲器在横向、纵向的修正距离比值为

当点火相位最优时需保证式(4 -29) 成立, 即

则由式(4 -29)、式(4 -31) 和式(4 -32) 可得

φ 角即为最优点火相位角, 按照此方位角激活脉冲推冲器时剩余误差最小, 工程应用中可将修正能力比值提前解算出来, 存储到飞行控制软件中, 飞行中根据需要实时进行查表插值解算。

4) 点火逻辑

当落点偏差值大于点火阈值时需要选定用于弹道修正的脉冲推冲器, 选择脉冲推冲器时需要解决两个方面的问题, 一是如何快速查找到所需脉冲推冲器, 二是要避免重复查询。在此将数组的概念引用到脉冲推冲器选择算法中,提出了一种采用数组方式对脉冲推冲器进行编号、按照编号顺序选择脉冲推冲器的点火逻辑方法。此外, 由于火箭弹加装修正舱段后其质心位置位于修正舱和尾翼之间, 研究表明脉冲力矩修正效果要优于脉冲力修正效果, 在此确定了上升段优先选择离弹顶最近的脉冲推冲器和下降段优先选择离弹顶最远的脉冲推冲器的基本选择原则。脉冲推冲器点火控制逻辑如下:

首先, 对脉冲推冲器进行数值编号, 以8 ×8 为例进行解释。脉冲推冲器的布局如图4 -6 所示, 在此定义离卫星接收天线最近的一圈为第1 圈, 脉冲推冲器的圈号随着与弹顶距离而增加。每圈的8 个脉冲推冲器按照与地磁测量组件之间的位置关系依次编号为1、2、…、8。至此, 每个脉冲推冲器有唯一的一个编号, 该编号以二维数组的形式表示, 以[3] [5] 为例, 代表了该脉冲推冲器位于第3 圈, 在该圈的排号为第5 个。

其次, 脉冲推冲器数组编号初始化。火箭弹发射后热电池过载激活, 弹道控制系统完成上电, 弹载计算机将每个数组编号都赋予0。

最后, 选择脉冲推冲器。脉冲推冲器选择流程如图4 -11 所示。

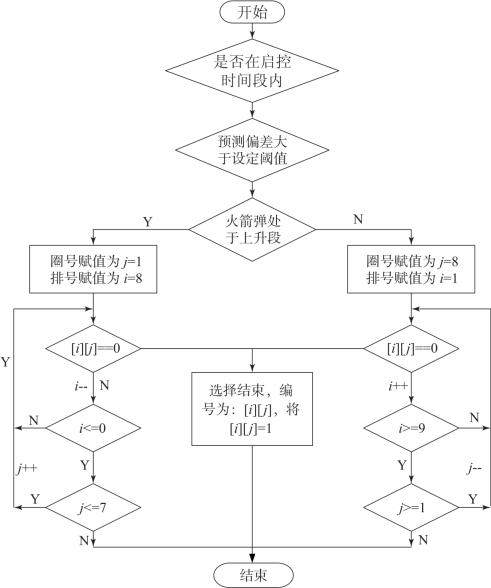
图4-11　脉冲推冲器选择流程

从图4 -11 可以看出, 采用脉冲推冲器进行弹道修正时首先要判断是否需要进行弹道修正, 当需要进行弹道修正时脉冲推冲器的点火逻辑按照飞行阶段的不同分为上升段点火控制逻辑和下降段点火控制逻辑两种情况。以上升段点火控制逻辑为例, 首先查找第1 圈是否存在尚未被使用的脉冲推冲器, 同一圈内按照序号升序排列方式依次进行查询, 当查找到未被使用的脉冲推冲器时将该数组的标志位置1, 这样保证了脉冲推冲器不会被重复选择, 至此一次查询结束。如果第1 圈内脉冲推冲器已全部被使用完, 则查询下一圈, 直至用完。火箭弹飞行中每进行一次弹道修正都需要执行该流程。采用该方法避免了每次都需要查询所有的脉冲推冲器, 节省了时间, 提高了查询速度。此外, 利用标志位置1 的方式, 避免了重复使用, 可进一步提高脉冲推冲器的弹道修正效能。

2.地面旋转点火试验验证

为了验证脉冲推冲器控制算法的正确性, 需要进行脉冲推冲器点火试验。为使脉冲推冲器地面点火试验与实际飞行过程中脉冲修正更为接近, 设计了地面旋转点火试验台, 试验台的结构布局如图4 -12 所示。

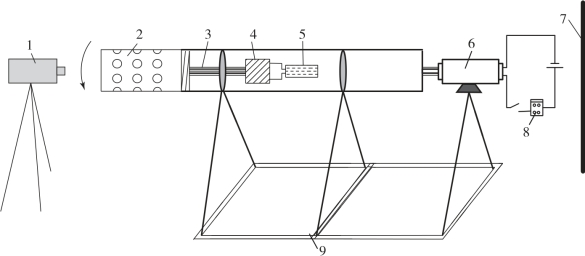
图4-12　脉冲推冲器性能参数验证试验台示意图

1—高速摄影机; 2—脉冲推冲器阵列; 3—电缆; 4—控制器; 5—热电池; 6—电动机;7—背景板; 8—控制板; 9—转台支架

从图4 -12 可以看出, 试验台由高速摄影机、脉冲推冲器阵列、控制器、热电池、电动机、控制板和背景板组成; 此外, 为了记录点火控制过程所产生的数据, 控制器内安装有存储卡, 用以记录过程数据。进行点火试验时脉冲推冲器阵列、弹载控制器和热电池在电动机的带动下随着转轴的旋转而转动, 电动机的转速通过控制板来调节。将一台高速摄影机放置在转轴延长线方向上,记录点火过程, 用以判断脉冲推冲器点火方位角是否正确。此外, 为了增加对比度, 在转台后面放置一块对比背景板。考虑到拍摄效果和拍摄时长, 试验时采取了500 帧的拍摄速度, 连续两张图片之间的时间间隔为2 ms。

为分析方便, 要求脉冲推冲器点火方位角为0°, 为保证旋转台的稳定, 点火时间间隔不小于0.3 s, 按照此要求进行了一组脉冲推冲器的点火试验, 随机选取了一个脉冲推冲器, 其工作过程如图4 -13 所示。

图4-13　某一个脉冲推冲器旋转工作过程

从图4 -13 可以看出, 图4 - 13 (a) 中脉冲推冲器随转轴在旋转, 图4 -13 (b) 中脉冲推冲器已产生了较大的火焰, 说明脉冲推冲器在两幅图片中的某点已经开始工作。图4 -13 (c)、(d) 中脉冲推冲器正处于工作状态,图4 -13 (d) 只有零星的火焰, 说明该时刻脉冲推冲器已经停止工作。从这5 幅连续的图中可以看出, 脉冲推冲器工作过程中产生的火焰一直冲上, 实际的点火方位角与设计值完全一致, 说明了脉冲推冲器点火控制算法的有效性。

3.阻力板控制技术

阻力板为弹道修正弹常用的一种执行机构, 依靠增加火箭弹的阻力实现射程偏差修正, 其修正方式为气动力修正的一种。采用阻力板进行弹道修正可以大大提高无控火箭弹的纵向密集度, 被认为是实现弹道修正最简单、最直接和成本最低的方式。课题组设计的阻力板为一次性展开执行机构, 一旦展开后将无法缩回进行二次或者多次修正, 阻力板射程修正效果完全取决于阻力板的展开时机, 展开时机不准确将导致射程偏差修正过量或者修正不足, 造成射程偏差较大, 降低纵向密集度, 所以射程修正弹最为关键的问题是确定阻力板的展开时机, 常采用的方法为数值积分的方法, 这种方法很难实现实时解算, 为提高阻力板的弹道修正效能, 需要对确定阻力板展开时机的算法进行深入研究。

1) 阻力板弹道修正原理

阻力板修正弹的工作原理是火箭弹发射前有意地进行 “远瞄”, 火箭弹发射后弹道修正系统实时地对弹体位置、速度和姿态信息进行测量, 实时预测纵向射程偏差和阻力板的修正能力, 当纵向预测偏差和阻力板的修正能力满足一定的关系时发出阻力板展开指令, 阻力板受控展开。阻力板展开后火箭弹受到的阻力增大, 火箭弹逐渐向目标点靠近, 直至落地。根据射程修正弹的工作原理绘制了射程修正弹的外弹道, 如图4 -14 所示。

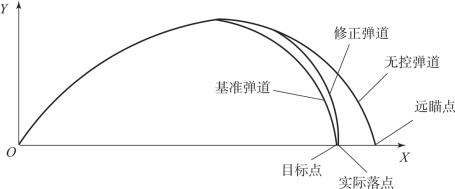
图4-14　射程修正火箭弹外弹道示意图

从图4 -14 可以看出, 对火箭弹不加以控制时火箭弹将命中远瞄点, 由于阻力板的修正作用火箭弹将落在目标点附近, 提高了火箭弹的纵向密集度。阻力板展开时机控制流程如图4 -15 所示。

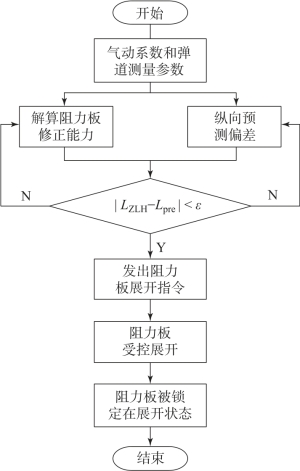
图4-15　阻力板展开时机控制流程

从图4 -15 可以看出, 为了有效实现弹道修正, 火箭弹飞行过程中弹载计算机需要实时地对射程偏差和阻力板的射程修正能力进行预测解算, 按照控制规律要求适时发出阻力板展开指令, 修正弹道将逐渐向基准弹道靠近直至命中目标。从射程修正弹的工作原理可以看出, 阻力板展开控制最为关键的是实时预测解算出落点偏差和阻力板的修正能力, 阻力板展开控制最为关键的问题是实时解算出阻力板的射程修正能力。由于弹载计算机性能有限, 要求控制算法简单、精度高。在确定阻力板的展开时机算法之前首先对阻力板的弹道修正模型进行介绍。

2) 阻力板射程修正模型

为了实时解算出阻力板的射程修正能力, 需要建立阻力板的射程修正模型, 为分析方便在此对阻力板做以下基本假设:

(1) 两片阻力板面积相同, 展开响应时间一致。

(2) 两片阻力板具有严格的面对称性。

(3) 阻力板产生的阻力与火箭弹弹轴平行。

(4) 阻力板展开后不会引起弹体滚转力矩、俯仰力矩和偏航力矩的变化。

根据外弹道学的知识可知, 阻力板展开后引起的附加阻力为

式中, ΔCx 为阻力板展开引起的附加轴向力系数, 阻力板没有展开时该值为0;FZLH为阻力板展开后对弹体产生的阻力。

进行射程修正能力解算时实际是将不同马赫数下阻力板展开前和展开后对应的轴向力系数代入式中进行数值积分并对最后的射程进行比较的过程。

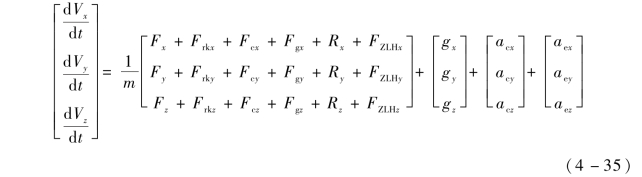
根据阻力板射程修正能力解算需要, 对加装阻力板的射程修正弹进行了气动数据计算。

绘制了阻力板展开前、后轴向力系数对比图, 如图4 -16 所示。

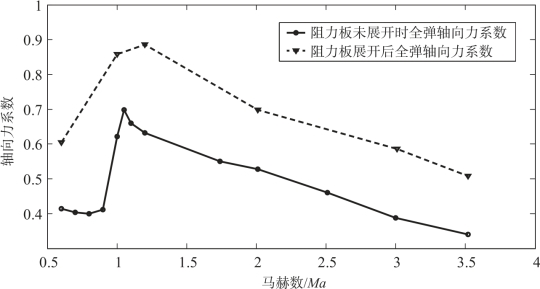
图4-16　阻力板展开前、后轴向力系数对比图

从图4 -16 可以看出, 阻力板展开后的轴向力系数明显大于阻力板展开前的值。阻力板展开前的轴向力系数在亚声速阶段基本保持不变, 在声速附近急剧上升, 在1.05Ma 处轴向力系数达到最高值0.697 7, 此后轴向力系数随着马赫数的增加而单调递减。阻力板展开后, 轴向力系数在声速之前随着马赫数的增加而增大, 在1.2Ma 处达到最大值0.886, 此后轴向力系数逐渐减小, 但在2Ma 之前这种减小的趋势并不明显。从图4 -16 还可以看出, 在不同马赫数下, 阻力板展开后的轴向力系数值增幅量不同, 2Ma 时轴向力系数从0.528 1 增加到0.847 5, 增幅量为0.319 4, 其他马赫数处增幅量相对较小,所以不能单纯地在阻力板前轴向力系数的基础上乘以一固定常数来代替阻力板展开后的轴向力系数。

采用四阶龙格-库塔法编制弹道解算程序, 以马赫数为自变量对轴向力系数进行线性插值, 在标准条件下, 计算了45°射角的弹道在不同射程处展开阻力板对应的修正能力, 如图4 -17 所示。

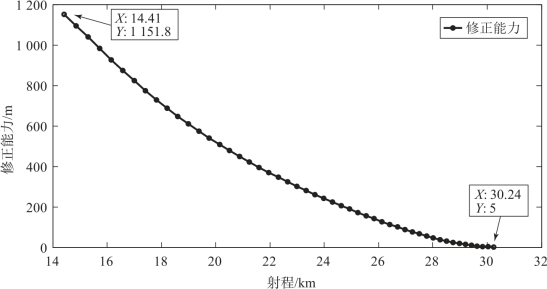
图4-17　不同射程处展开阻力板对应的修正能力

从图4 -17 可以看出, 在不同的射程处展开阻力板时对应的修正能力不同, 射程为14.41 km 时其修正能力为1 152 m, 随着射程的增加其修正能力逐渐衰减, 在短距离内阻力板修正能力可以认为是线性衰减的, 但对于整条弹道来说, 这种衰减的趋势类似于开口向上抛物线的左侧, 为了确定阻力板的展开时机可以利用阻力板的这种修正能力分布特点。

3) 阻力板展开时机

由前面分析可知, 确定阻力板展开时机最关键的问题是实时解算出阻力板的修正能力, 最常用的方法是采用数值积分的方法, 该方法对于弹道参数初始误差较为敏感。此外, 采用该方法进行修正能力解算时需耗时几秒甚至十几秒, 无法满足阻力板展开时机实时性的要求, 所以数值积分方法工程应用性不强。胡荣林等人提出了利用最小二乘拟合计算弹丸纵向加速度, 同时假设加速度值和弹着点弹道倾角为恒定值, 利用弹道积分计算阻力板修正能力, 控制阻力板的展开, 这种方法简化了计算量, 但是计算精确度差。本书根据阻力板的修正能力分布特点提出了一种发射前提前解算阻力板修正能力、发射后根据阻力板的修正能力数值表线性插值解算阻力板修正能力的方法, 这种方法不需要进行循环积分, 一次插值便可计算出在不同射程下的阻力板修正能力, 可降低计算时间。下面对阻力板修正时机的算法进行深入研究。

(1) 发射前解算修正能力数值表。

为了准确确定阻力板的展开时机, 在火箭弹发射前需要根据实际气象信息和炮位、目标点坐标解算出阻力板的修正能力。采用射程修正弹进行射击时,需要有意地进行“远瞄”, 此“远瞄”距离称为射程扩展量。当按照增加射程扩展量后对应射程解算的射击诸元进行射击时, 受随机误差的影响无控火箭弹的射程散布是随机的, 理论上来说需要计算不同弹道对应的阻力板修正能力,但由于阻力板的修正能力在小范围内是线性衰减的, 因此只需要计算几条有代表性的弹道对应的阻力板的修正能力即可, 使用时可利用线性插值获得相近弹道的阻力板修正能力。

当射程扩展量确定时, 需要选择具有代表性的弹道, 所选弹道更接近于基准弹道时对应的阻力板修正能力会导致修正过量, 所选弹道远大于射程扩展量对应的弹道时, 修正能力线性衰减的特性将不再适用, 进行线性插值时将会出现方法误差。当射程扩展量为d 时, 根据数理统计知识, 无控弹着点介于d/2 ~ 3d/2 的概率为68.26%, 包括了绝大多数弹道, 在此选择计算射程扩展量为d/2 和3d/2 对应弹道的阻力板修正能力, 经验表明这种选择是可行的、有效的。

由图4 -18 可知, 火箭弹在标准条件下45°射角对应的阻力板修正能力可达1 151.84 m, 按照黄义等人所提射程扩展量计算方法, 如果以标准条件下45°射角对应的坐标为目标点使用射程修正弹时, 需要 “远瞄”的距离为600 m 左右。以射程扩展量600 m 为例对阻力板修正能力数值表的计算进行说明, 具体计算流程如图4 -18 所示。

其中, ti 表示阻力板展开时刻设定值, Δt 表示相邻两次阻力板修正能力计算的时间间隔, Tfirst表示阻力板第一次展开的设定时刻。从图4 -18 可以看出,射程扩展量为600 m 时需要计算射程扩展量为300 m 和900 m 对应弹道的阻力板修正能力数值表。由于计算原理相同, 只介绍射程扩展量为300 m 的弹道对应的阻力板修正能力。

当已知炮位和目标点的坐标以后, 可计算炮位和目标点之间的距离, 设此距离为L 。首先, 利用弹道解算程序解算出远瞄300 m 射程对应的射角, 记为A0 ; 其次, 以射角A0 为输入量进行弹道积分, 当弹道积分时间小于设定值ti时表示火箭弹无控飞行, 记录此状态下最后一点的射程, 设为xi ; 然后, 当弹道积分时间大于等于设定值ti 时表示阻力板展开, 开始进行控制飞行直至落地, 设弹着点对应的射程为Li , 则xi 射程处对应的阻力板修正能力为

记为(xi,li) , 至此一组射程- 阻力板修正能力计算结束。按照同样的方式可循环解算同一弹道在不同时刻展开阻力板对应的修正能力。间隔取得越小, 数组个数越多, 越精确, 但是数据量会急剧增加, 这可根据弹载计算机的存储量决定。为了插值解算方便, 射程扩展量为300 m 和900 m 计算的阻力板修正能力数组个数应相同, 设这个数为N 。将射程扩展量为300 m 和900 m 计算的射程-修正能力数组分别记为(xnear[i], lnear[i])和(xfar[i], lfar[i]), 其中i=1,2, 3, …, N。

(2) 在线实时解算修正能力

前面给出了阻力板修正能力的计算方法, 完成修正能力解算以后需要将修正能力数值表上传到弹载计算机上, 用于阻力板的展开控制。为使阻力板的修正能力解算值更为精确, 在进行解算前需要对修正能力数值表进行预处理, 然后用于控制阻力板的展开。由于阻力板较多在过弹道顶点以后展开, 可在弹道顶点处对修正能力数值表进行处理、选择。是否到达弹道顶点可根据弹体法向速度Vy 值来判断, 当Vy ＜0 时说明弹丸已过弹道顶点。修正能力数值表处理、选择及对阻力板的展开控制流程图如图4 -19 所示。

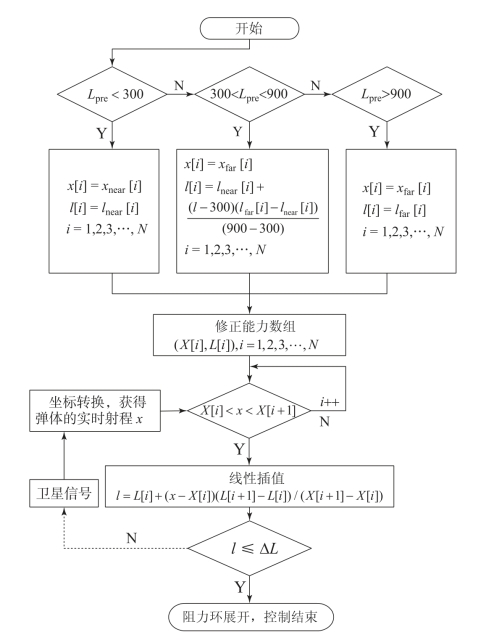
图4-19　使用修正能力数值表的阻力板展开控制流程图

从图4 -19 可以看出, 对修正能力数值表使用时先进行预处理然后进行插值解算。假设由Vy 值判断得知某时刻火箭弹已到达弹道顶点则飞行控制模块进入阻力板展开控制环节。假设弹道顶点处的射程预测偏差为Lpre, 如果满足Lpre ＜300 的条件说明当前弹道与射程扩展量为300 m 的弹道更为接近, 阻力板修正能力相当。为使用方便, 将扩展量为300 m 弹道对应的射程-修正能力数组(xnear[i], lnear[i]) 赋予另一新数组(X[i],L[i]) 。如果此时的预测值大于300 m 同时小于900 m, 说明当前弹道与射程扩展量为Lpre的弹道相似, 由于射程修正能力的变化基本上是线性的, 利用式 (4 -37) 可计算射程扩展量为Lpre弹道的阻力板修正能力。

计算出修正能力后同样将插值后的射程- 修正能力数组赋予(X[i],L[i]) 。如果此时的预测值大于900 m, 可将修正能力直接赋予同一数组, 原因同上。一旦完成修正能力数值表预处理后弹道修正系统在剩余弹道中不再对修正能力数值表进行处理。

对修正能力数值表处理、选择以后, 假设t 时刻的射程为x, 首先搜索射程x 在修正能力数值表中的位置, 当确定射程所处区间后, 可根据式(4 -38)插值计算射程为x 处的阻力板的修正能力l。

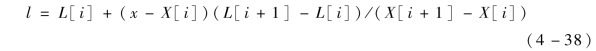
当阻力板的修正能力小于等于此时的预测偏差ΔL 时发出阻力板展开指令,如果不满足条件, 则循环进行计算, 直至满足展开控制要求, 一旦发出阻力板展开指令后整个控制流程结束。

综上分析可以看出, 阻力板展开时机的算法分为发射前提前解算阻力板修正能力和发射后在线解算两部分, 采取这种方式缩短了阻力板修正能力的在线计算时间, 解决了阻力板修正控制实时性的问题, 工程应用性更强。为了验证阻力板展开时机算法的精确性, 进行了阻力板展开控制仿真验证和试验验证。