导引控制技术优化方案

1.摄动落点预测

弹道摄动理论是用来描述常规炮弹在基准弹道附近运动状态的一种理论,最早由钱学森提出, 在高性能电子计算机出现之前该理论常用于计算弹道导弹的实际弹道, 随着计算机技术水平的发展, 这种方法在导弹弹道计算问题上已经被淘汰。但是, 对于常规小口径火箭弹来说, 受整体成本及空间的限制, 选配的弹载计算机性能有限, 还不能用弹道模型预测等计算过程复杂、耗时较长的方法预测解算火箭弹弹道参数。为了提高弹道修正系统的制导精度, 本节在研究分析摄动理论的基础上创新性提出了适合于弹道修正弹的落点预测算法。

1) 摄动理论

基准弹道是指根据指定的弹体结构参数、气象条件和气动系数解算的一条有着特定的飞行程序和飞行状态的确定性弹道。火箭炮武器系统进入发射阵地以后, 火控系统便可根据目标点坐标和气象信息采用数值积分的方法解算出发射点与目标点之间的基准弹道。火箭弹的总体参数、气动系数及发射环境与测量值相同时火箭弹将沿着基准弹道飞行直至命中目标。然而, 在火箭弹发射过程中由于随机干扰的客观存在, 例如弹道随机风、弹体加工误差, 扰动弹道(实际弹道) 将偏离基准弹道, 如果随机干扰较小, 实际弹道将在基准弹道附近摄动并保持不大的距离, 这就是摄动理论的基本内涵。

采用摄动理论进行实际弹道的弹道预测时可以基准弹道为基础进行线性化处理, 实际弹道经过线性化处理以后描述弹体实际运动的运动方程就变成了变系数的线性微分方程, 当获得相应的参数变量和系数时便可对弹道进行预测,这就是摄动落点预测的基本思想。摄动落点预测主要解决的问题是如何根据火箭弹持续变化的状态和弹道环境解算出不同时刻的预测系数及如何确定将系数和相应的弹道参数联合起来对落点偏差进行预测。

2) 摄动制导应用

摄动理论最早用于确定导弹的发动机关机时间, 导弹精确命中目标的条件是实际落点与目标点之间的横向偏差和纵向偏差同时为零, 如果对导弹发动机关机以后的弹道不加以控制, 导弹被动段的弹道和落点情况将完全取决于发动机关机时刻的参数, 为了达到精确命中目标的要求需要对关机点关机时间进行控制, 弹道摄动理论就是在这种客观需求下产生的。弹道摄动理论将发动机关机点参数偏差与火箭弹落点偏差之间的关系联系起来, 当发动机的工作状态满足精确命中目标的要求时发出发动机关机指令, 这种方法能够消除初始扰动引起的偏差, 进一步提高导弹的射击精度。

导弹发动机关机以后剩余弹道将受到何种形式或者量级多大的干扰无从得知, 摄动理论应用的假设条件是: 火箭弹在剩余弹道受到的干扰为零, 在此假设条件下火箭弹的射程和横向距离都可以表示成关机点弹道参数的函数:

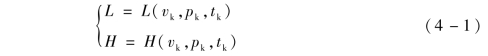
从式(4 -1) 可以看出, 导弹的射程和横向偏差取决于发动机关机点的弹道参数。关机点弹道参数与标准条件一致时火箭弹能够精确命中目标, 如果关机点参数与标准条件存在偏差时, 这些弹道参数偏差造成的最终的落点偏差可以展开成关机点参数偏差的泰勒级数:

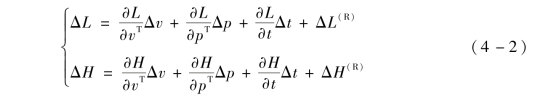
式中,

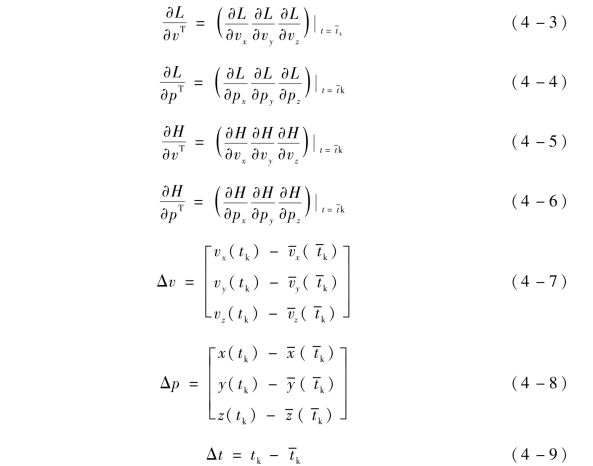
式中, ΔL(R) , ΔH(R) 为泰勒级数的高次项; 符号 “ - ”表示基准弹道参数; 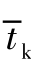为基准弹道关机时间; tk 为实际关机时间; ∂L/∂vT 、∂L/∂pT 、∂L/∂t 为射程对应的参数变量在基准弹道关机点处的偏导数; ∂H/∂vT 、∂H/∂pT 、∂H/∂t 为横向偏差对应的参数变量在基准弹道关机点处的偏导数; Δv 为实际弹道速度和基准弹道速度之间的差值;Δp 为实际弹道位置和基准弹道位置之间的差值。当基准弹道确定以后, 射程和横向偏差对弹道参数的偏导数都是确定的常数, 弹道参数偏差可以通过弹载测量设备测得弹道参数与基准弹道参数偏差相减得出。

速度和位置信息是发动机关机时间的函数, 从式 (4 -1) 可以看出, 关机时间越早, 实际射程与标准射程的差距越大, 随着发动机关机时间的延迟实际射程越来越接近于标准射程, 当实际射程与标准射程相等时关闭发动机能保证确保命中目标。∂L/∂v、∂L/∂p 和∂L/∂t 需要发射前解算出来并存储到弹载计算机上, 当火箭弹进行导航控制解算时, Δv 和Δp 可实时求出, 可以直接采用式(4 -1) 作为关机方程, 这种方法简化了弹上解算过程, 但是只能保证射程偏差为零, 横向偏差需要单独进行解算摄动预测控制, 这就是摄动理论在导弹制导上的应用。

3) 摄动落点预测解算

摄动理论是根据弹道导弹的飞行控制需求发展起来的, 但是对于常规火箭弹来说并不能照搬这种方法, 原因如下:

(1) 常规火箭弹为全备弹, 发动机关机时间不可控, 不能采用控制火箭发动机关机时间的方法来保证射程偏差为零。

(2) 常规火箭弹的整条弹道都在大气层内, 随机干扰对于弹道的影响是持续存在的, 为了提高火箭弹射击精度, 仅通过控制发动机关机时间来进行落点控制无法满足射击精度需求, 为了确保射击精度, 整个飞行弹道都需要进行弹道修正。

(3) 弹道导弹上安装了惯性测量组件, 控制系统可以获得导弹任意时刻的位置、速度和姿态等信息, 受弹体成本和空间限制的常规火箭弹无法提供如此全面、高精度的弹道参数, 无法将已有的研究成果用于弹道修正火箭弹的导引控制。

(4) 弹道导弹具有较强的修正能力, 弹道导弹的射击方向与发射装置和目标点之间的连线方向重合即可, 导弹飞行中控制系统将其严格控制在发射平面内直至命中目标。弹道修正火箭弹修正能力有限, 无法按照导弹的控制方式进行弹道修正, 需要根据常规火箭弹的弹道特点选择横向导引方法。

(5) 弹道导弹发动机关机时间可控, 实际飞行时间与标准飞行时间能够保持一致, 可以采用时间作为自变量对系数和弹道参数偏差量进行计算。常规火箭弹关机时间不可控, 火箭弹飞行时间为随机变量, 采用时间作为自变量时将会出现实际弹道参数和基准弹道参数不匹配的现象。

基于以上5 方面的原因, 无法将弹道摄动理论直接挪用到弹道修正火箭弹上。在此以弹道摄动理论为基础提出针对弹道修正火箭弹的摄动落点预测算法。摄动落点预测算法的思想是将整条弹道分成若干段, 每一段的起始时刻都看成是发动机关机时间点, 各个点处弹道参数偏差对落点偏差造成的影响和关机点弹道参数偏差造成的影响相似, 以基准弹道为基础在相应的点进行泰勒级数展开, 以射程为自变量通过线性插值的方法可以预测解算弹道上每个点处弹道参数偏差对于落点偏差的影响, 弹道修正控制系统可以随时对落点偏差进行修正, 可以避免弹道末段需用过载较大的情况出现。

摄动落点预测算法按照计算流程的先后分为基准弹道计算、敏感因子计算和弹上落点偏差预测解算三个阶段, 摄动落点预测解算过程流程图如图4 -5所示。

从图4 -5 可以看出, 摄动落点预测分为地面提前解算和弹载计算机实时解算两部分, 地面火控计算机主要完成基准弹道和敏感因子的计算, 弹载计算机用于完成最后的偏差解算。

图4-5　摄动落点预测解算过程流程图

(1) 基准弹道计算。

基准弹道是发射点至目标点之间的一条基准弹道, 由弹体参数、气动系数和气象信息唯一确定。火箭弹沿着基准弹道飞行时无须进行弹道修正便可命中目标, 但是随机干扰的客观存在决定了火箭弹不可能完全沿着基准弹道飞行。摄动落点预测是以基准弹道为基准进行泰勒级数展开的, 弹道修正系统的目标就是将实际弹道修正到基准弹道附近, 基准弹道计算是否准确直接影响到预测算法的精度和控制系统的修正效能, 在此对基准弹道的计算过程进行研究。

进行基准弹道解算需要建立弹道模型, 根据弹道模型采用弹道方程将弹道的运动规律描述出来, 相关内容可参照外弹道书籍, 在此不再赘述。下面只对基准弹道解算过程进行分析, 解算基准弹道首先要确定解算的方法, 其次要确定射击诸元的解算方法, 最后要选择合适的基准弹道参量进行输出。

①解算方法。计算基准弹道就是求解弹道方程的过程, 弹道方程是一系列变系数的数学表达式, 由于弹道方程的系数一直处于变化之中, 很难得到解析解, 一般采用数值积分法求解弹道方程得出不同点的弹道参数, 其中龙格- 库塔法具有精度高、程序简单和改变步长方便等优点, 常用于弹道方程的解算。最常用的是四阶龙格-库塔法, 若已知在点n 处的值(tn,y1n,y2n,…,ymn) , 则求得n + 1 处的函数值的龙格-库塔方程为

式中,

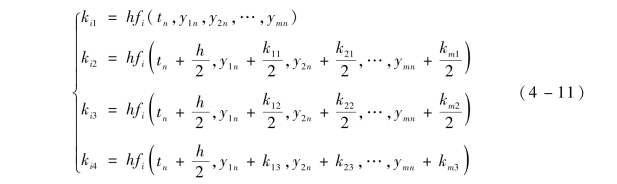
式中, h 为积分步长, 积分步长越小计算精度越高, 但是选择小的积分步长会增加弹道解算时间, 需要根据制导控制需求和火控计算机的性能选择积分步长。基准弹道解算方法给出了对弹道方程进行数值积分的方法, 但是在进行解算之前需要确定射击诸元作为基本输入, 下面将对射击诸元的解算方法进行研究。

②确定射击诸元的方法。确定射击诸元是指根据已有的总体参数、气动系数和气象信息解算出射角和射向的过程。按照计算顺序分为以下几个步骤:

a.根据发射点和目标点坐标信息解算出炮位与目标点之间的连线和真北方向之间的夹角, 定义这个角度为基准射向, 记为A0 。同时解算出炮位与目标点之间的距离, 即火箭弹需要达到的射程, 记为L。

b.设定火炮发射火箭弹时存在最大射程角φmax 和最小射程角φmin , 以基准射向A0 为发射方向, 分别以φmax 和φmin 为初始射角计算得到最大射程Lmax 和对应的横向偏差Hmax 、最小射程Lmin 和对应的横向偏差Hmin , 判断火箭弹目标射程L 是否在最大射程和最小射程范围内, 即是否满足

当不满足这一判断条件说明目标射程在火箭弹的能力范围以外, 终止发射火箭弹。当目标射程L 满足式(4 -11) 则执行下一步。

c.设为射角,A = A0 - ΔA1 为射向解算弹道方程, 假设解算出的射程和横向距离分别为L1 和H1 , 首先判断解算的射程和目标射程之间的关系是否满足| L - L1 | ≤εL 和| H - H1 | ≤εH 的条件, 其中εL、εH 为设定的阈值, 如果该条件得到满足则停止搜索; 如果不满足| L -L1 | ≤εL 和| H - H1 | ≤εH 的条件, 判断L 和L1 之间的关系, 如果L ＞L1 继续向上搜索, 否则向下搜索。

d.以向上搜索为例, 设ΔA2 = arctan(H1/L1) , 以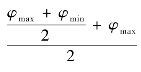为射角, A = A0 - ΔA1 - ΔA2 为射向解算弹道, 假设对应的射程和横向偏差分别为L2 和H2 , 再次判断解算的射程和目标射程之间的关系| L -L2| ≤εL ,| H -H2| ≤εH,如果满足条件停止搜索, 如果不满足条件重复步骤d, 直至满足条件。

a~d 给出了解算射角射向的详细步骤, 在执行过程中需要特别注意三点:一是设置合适的终止条件; 二是搜索射角、射向过程中每一步都改变了射向,要注意气象的利用方式; 三是要选择合适的积分步长。

③基准弹道的输出。基准弹道信息包括位置、速度、姿态和过载等, 采用摄动落点预测算法进行落点预测解算时只用到位置和速度参数, 所以, 仅保留基准弹道的位置和速度信息即可。此外, 要确定合适的基准弹道输出间隔, 间隔太大进行线性插值解算时会降低运算精度; 间隔太小会增加数据量, 占用弹载计算机更多的内存空间。

(2) 敏感因子计算。

落点预测敏感因子是指弹道参数偏差对于落点偏差的影响程度, 是一无量纲量, 某一弹道参数偏差对落点偏差造成的影响越大说明落点偏差对于该弹道参数越敏感, 敏感因子相对就会较大, 反之敏感因子会很小。造成落点偏差的影响因素较多, 主要有位置、速度和姿态角, 在某一弹道点处可能只有一个弹道参数存在偏差, 也可能多个弹道参数同时存在偏差; 此外, 在某一射程处落点偏差对于弹道参数的敏感程度不同, 在不同射程处对同一弹道参数的敏感程度也是不同的, 弹道参数偏差对于落点偏差的影响有可能是独立的也有可能相互制约, 需要分为不同的情况进行讨论。弹道修正火箭弹在飞行过程中将受到持续的扰动, 为了提高射击精度全弹道都需要进行导航与控制, 因此需要计算全弹道的敏感因子。进行敏感因子计算首先要选择落点偏差的参数变量, 其次要确定计算方法, 此外, 还需要确定敏感因子的级数和步长。

①选择参数变量。选择参数变量是指确定影响射程和横向偏差相关量的过程。火箭弹在空间的运动可以分解成垂直方向的运动和水平方向的运动。

火箭弹在垂直方向的运动方程为

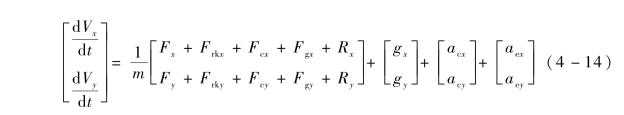
从式(4 -13) 和式(4 -14) 可以看出, 火箭弹在垂直方向的运动可以用纵向速度、法向速度和弹道高进行描述, 则射程偏差可以表示成纵向速度偏差ΔVx 、法向速度偏差ΔVy 和弹道高偏差Δy 的函数。

火箭弹在水平方向的运动方程为

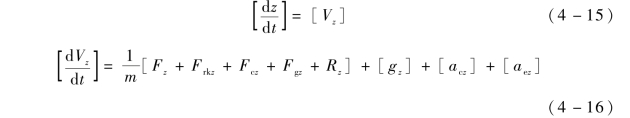
从式(4 -15) 和式(4 -16) 可以看出, 火箭弹在水平面内的运动可以用横向位置和速度进行描述, 则横向落点偏差为横向位置偏差Δz 和横向速度偏差ΔVz 的函数。

②计算方法。火箭弹飞行中的实际弹道参数由基准弹道参数与弹道参数偏差组成, 则射程为x 处的实际弹道参数可以表示为

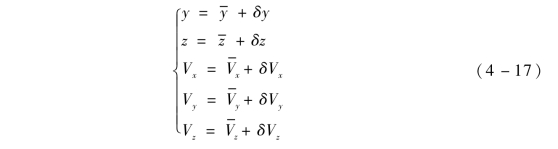
由式(4 -17) 可以看出, 如果弹道参数偏差为0, 则射程x 处的实际的弹道参数与基准弹道参数是相同的, 火箭弹在剩余弹道中不再受到新的干扰时将沿着基准弹道飞行最终精确命中目标, 即纵向偏差和横向偏差同时为0。火箭弹实际飞行过程中不可能保证弹道参数偏差一直为0, 假设在射程x 处存在弹道高程偏差δy, 则以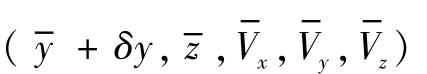代替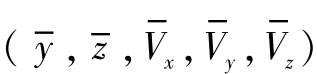 作为输入量代入到弹道方程中可以解算出存在弹道高程偏差δy 的对应落点坐标, 将该落点坐标减去基准弹道落点坐标即为射程x 处弹道高程偏差δy 引起的落点偏差, 设这一偏差为δLy , 则射程x 处落点偏差对于弹道高的敏感程度为δLy/δy,记为∂L/∂y, 该值即为射程x 处纵向偏差ΔL 对于高程δy 的敏感因子。同理可得射程偏差对于纵向速度偏差δVx 和法向速度偏差δVy 的敏感因子以及横向落点偏差对于横向速度偏差δVz 和横向位置偏差δz 的敏感因子。单个弹道参数的敏感因子都可以参照上述过程进行计算, 在此不再重复进行介绍, 下面对高阶或多个同时存在偏差对应敏感因子的计算过程进行介绍。

假设在射程为x 处同时存在高程偏差δy 和纵向速度偏差δVx , 则以( +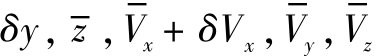) 代替作为输入量解算弹道方程可以得到同时存在两种偏差时对应的落点坐标, 将该落点坐标减去基准弹道落点坐标便为射程x 处高程偏差δy 和纵向速度偏差δVx 共同作用引起的落点偏差, 假设δy和δVx 引起的射程偏差为δLyVx , 则射程偏差对于弹道高偏差和纵向速度偏差的敏感程度为

式(4 -18) 即为射程x 处纵向偏差ΔL 对于高程差δy 和纵向速度偏差δVx的敏感因子。采用同样的方法可得射程偏差对于同时存在多个弹道参数偏差的敏感因子, 同理可以计算更高阶弹道参数敏感因子。

③步长的选取。敏感因子计算方法中给出了单一弹道点处弹道参数敏感因子的计算过程, 但只能用于该射程处的落点偏差, 弹道修正火箭弹全弹道都需要进行导引控制, 仅计算一点的弹道参数敏感因子无法满足制导控制需求, 因此需要将计算一点的弹道参数敏感因子扩展到整条弹道, 但是由于弹载计算机内存有限, 不可能对每一点的敏感因子都进行计算, 可以选择特征点的方式来解决这一问题。选取的特征点越多进行线性插值时准确度越高, 但是所需计算的数据量成倍数地增加, 这种情况不仅会增加敏感因子的解算时间还会占用弹载计算机上更多的内存, 影响弹载计算机的运算性能, 所以弹道特征点需要根据弹载计算机的性能而定。敏感因子计算完后可以按照式 (4 -19) 给定的格式进行保存。

(3) 弹上落点偏差计算。

落点偏差解算是以火箭弹当前状态为输入量与标准状态进行比较得出状态量偏差并根据状态偏差量和敏感因子之间的关系解算出落点偏差量值和方向的过程。为了满足弹道修正对落点预测实时性的要求, 要求偏差解算方法简单、计算过程少。落点偏差预测解算分为解算弹道参数偏差量、求解对应的敏感因子和计算相应系数处理等过程。

①解算弹道参数偏差量。弹道参数偏差量是指在同一弹道点处实际弹道和基准弹道的差值。弹道修正火箭弹内集成了卫星导航接收机和姿态测量模块, 可以对弹体的速度、位置和转速进行测量。摄动落点预测所需要的弹道参数输入量为弹体的位置偏差和速度偏差, 为了解算出弹道参数偏差需要将实际弹道与基准弹道转化到同一个坐标系内, 同时需要选取合适的参考变量。

火箭弹发射前将基准弹道和敏感因子装定到弹载计算机上, 火箭弹发射以后卫星导航接收机实时测量弹道位置和速度信息, 假设某一时刻弹道参数为xe、ye、ze、Vxe、Vye、Vze, 根据地球坐标系和发射坐标系之间的关系式, 则对应的发射系内的弹道参数为x 、y 、z 、Vx 、Vy 、Vz 。火箭弹用于打击地面固定目标, 目标点和发射点之间的相位和距离是确定的, 不会随着发射环境和火箭弹状态的改变而改变, 在此选用射程为自变量和参考变量。设射程为x =x- 时, 对应的基准弹道参数为, 则该弹道点的弹道参数偏差为

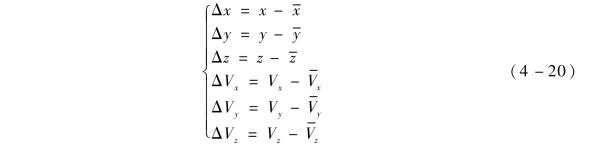
②求解对应的敏感因子。求解对应的敏感因子是以射程为自变量和参考变量求解得出当前弹道参数对应敏感因子的过程。

敏感因子采用式(4 -19) 的方式进行保存时, 射程与弹道参数的相关敏感因子是一一对应的, 利用线性插值的方法可以求解不同射程处弹道参数对应的敏感因子。设射程为x 处弹道参数对应的敏感因子为

③解算落点偏差。由本条①②可知, 射程x = x- 处对应的弹道参数偏差为式(4 -20), 相应的敏感因子如式(4 -21) 所示。弹道参数偏差与相应的敏感因子相乘便是该弹道参数引起的落点偏差, 则在x = 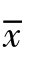射程时各个弹道参数偏差对落点偏差造成的影响为

纵向落点偏差只与纵向速度偏差ΔVx 、法向速度偏差ΔVy 和高程偏差Δy及交联项有关, 则弹道参数引起的纵向落点偏差和为

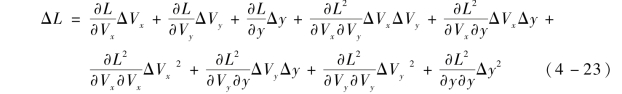
横向落点偏差由横向位置偏差Δz 和横向速度偏差ΔVz 引起, 两者几乎没有任何交联, 弹道参数偏差引起的横向落点偏差和为

从摄动落点预测的整个解算过程可以看出, 地面火控计算机完成了落点预测的大部分任务, 弹载计算机只需要进行简单加减运算便可解算出落点偏差,弹上计算过程大大简化, 提高了落点预测的实时性。

2.追踪制导技术

追踪制导律利用弹上的导引头或目标探测器接收目标信息确定弹目之间的相对位置, 并形成控制信号, 自动将弹丸导向目标。根据目标探测器固连的位置不同, 追踪制导律又分为速度追踪制导律与弹体追踪制导律。

1) 速度追踪制导律

速度追踪制导律在弹丸攻击目标过程中, 力图使弹丸的速度矢量v 始终指向目标, 其工程实现也比较简单, 将激光探测器安装在风标头上, 风标机构则与弹体采用万向节连接。由于弹上没有导引头, 只有风标头和探测器组件, 故成本较低。

在弹丸飞行过程中, 风标机构能使激光探测器光轴与弹丸质心速度矢量方向保持一致, 因而激光探测器在随弹丸一起滚转的同时, 始终能够追随弹丸的速度矢量, 确保激光探测器的光轴与弹丸质心速度矢量保持同轴。

由于激光探测器的光轴与风标头的指向平行, 而风标头的指向始终沿着弹丸速度矢量方向, 故可利用测得的目标与激光探测器光轴之间的夹角 (误差角) 作为控制指令对弹道进行修正。

速度追踪制导律在攻击目标的导引过程中, 力图消除弹丸速度矢量且与弹目视线之间的偏差。

2) 弹体追踪制导律

弹体追踪制导律在弹丸攻击目标过程中, 力图使弹体纵轴始终指向目标,其工程实现最为简单, 只需将激光探测器直接固连在弹体上即可。

它采用激光探测器测量弹目视线与弹轴的偏差角, 形成控制指令对弹道进行修正。