如何利用仿真辅助技术提升工作效率？

2023-06-15 历史故事版权反馈

【摘要】：图3-48不同导航数据更新率下仿真得到的弹药射击精度从图3 -48 可知, 随着导航数据更新率的增大, 纵向标准差和CEP 呈现出逐渐增大的变化趋势, 受随机干扰的影响, 中间会出现振荡。

制导子系统的特性会对弹药精度产生影响, 分析制导子系统对精度有重要影响的特性, 并对该特性进行严格的采购控制, 或采用影响补偿措施加以削弱, 将非常有助于提升弹药的落点精度。

1.卫星定位模块特性对射击精度影响的仿真分析

在卫星定位模块的性能指标中, 定位精度、定速精度、启动时间、导航数据更新率等技术指标可能会对制导迫击炮弹的射击精度产生影响。

(1) 定位精度和定速精度对射击精度的影响。定位精度和定速精度通常是相关的, 因此, 定位、定速精度状态取值时按表3 -6 进行, 对4 种状态分别进行模拟打靶, 得到的打靶结果见表3 -6。

表3-6　不同定位、定速精度下射击精度

pagenumber_ebook=114,pagenumber_book=98

从表3 -6 可知, 定位精度和定速精度对射击精度有重要影响, CEP 随着定位、定速误差的增大而增大。因此, 从设计的角度考虑, 在选用卫星定位模块时, 应根据弹药的精度指标, 在成本允许的情况下, 尽可能选用定位精度和定速精度较高的卫星接收机。

(2) 启动时间对射击精度的影响。启动时间对射击精度的影响与飞控模块启控时间相关, 当启动时间小于飞控模块启控时间时, 启动时间对射击精度没有影响, 当启动时间大于飞控模块启控时间时, 启动时间对射击精度的影响与飞控系统启控时间对射击精度的影响相同。如前所述, 为减小启动时间, 卫星定位模块通常会采用预装星历的热启动方式, 星历新鲜度小于等于10 min时, 使卫星定位模块启动时间小于等于10 s。

(3) 导航数据更新率对射击精度的影响。分别设置卫星定位模块导航数据更新率为50 ms、100 ms、…、1 000 ms, 定位误差标准差统一设为10 m,定速误差标准差统一设为0.4 m/s, 通过模拟打靶得到不同导航数据更新率下弹药的射击精度, 如图3 -48 所示。

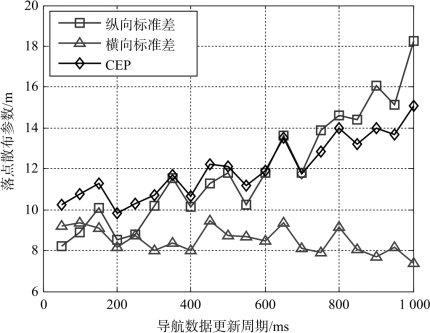
pagenumber_ebook=115,pagenumber_book=99

图3-48　不同导航数据更新率下仿真得到的弹药射击精度

从图3 -48 可知, 随着导航数据更新率的增大, 纵向标准差和CEP 呈现出逐渐增大的变化趋势, 受随机干扰的影响, 中间会出现振荡。而横向标准差基本不受导航数据更新率的影响。目前, 卫星定位模块的导航数据更新率一般在1 ~10 Hz。

2.舵机模块特性对射击精度影响的仿真分析

根据弹道控制原理, 舵机应在合适的时间将舵片偏转到制导指令规定的角度, 因此, 时间和角度控制对舵机而言至关重要。实际上, 舵机作为实物在动态控制中存在延迟、超调和衰减等现象, 因此, 在控制中往往将舵机模块看成一阶或二阶系统。

为掌握舵机的动态特性, 通过仿真计算机和负载模拟器对舵机进行仿真测试, 仿真计算机输入舵控指令信号到舵机, 通过负载模拟器测量实际舵偏值, 通过对比舵控指令和实际舵偏曲线获取舵机特性。图3 -49 所示为舵控幅值设定为7°、舵片负载设定为2 N·m 时的扫频特性曲线。从图3 -49 可以看出, 舵机实际工作时确实存在幅值衰减和相位延迟, 幅值衰减相对较弱。

下面重点分析舵偏延迟对射击精度的影响。舵偏延迟会使舵机控制力的方向产生偏差, 导致弹道修正方向出现混乱, 而弹道修正方向的混乱又会导致舵机弹道修正能力的不必要消耗, 进而对射击精度产生影响。比如不存在横向偏差, 舵机进行纵向修正时, 舵偏延迟导致舵机控制力存在横向分量, 造成新的横向偏差, 最终影响到射击精度。

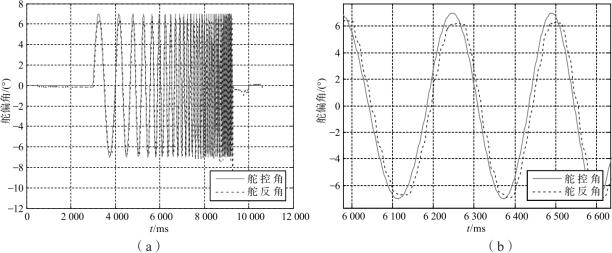
pagenumber_ebook=116,pagenumber_book=100

图3-49　舵控舵反曲线(舵控幅值7°,负载2N·m)

(a) 全局图; (b) 局部放大图

基于舵偏延迟的特点, 将舵偏延迟分别设定为2 ms、4 ms、6 ms、8 ms、10 ms、12 ms、14 ms、16 ms、18 ms、20 ms 等10 个常值, 通过模拟打靶得到弹药射击精度结果, 如图3 -50 所示。

pagenumber_ebook=116,pagenumber_book=100

图3-50　不同舵偏延迟对应的射击精度

从图3 -50 可知, 射击精度随着舵偏延迟的增大而逐渐增大。进行简易制导迫击炮弹设计时, 应该通过软件弥补舵偏延迟造成的不利影响。

3.飞控模块特性对射击精度影响的仿真分析

飞控模块受弹载计算机容量、速度和解算时间限制, 其对飞行控制算法的解算精度通常低于地面高性能计算机的解算精度。随着微处理器、微控制器和高速小型计算设备的发展以及制导控制算法的不断改进, 飞控模块的计算结果与全数字仿真所采用的计算机结果目前基本能够做到一致。

图3 -51 和图3 -52 所示为同等输入条件下, 仿真计算机解算结果与某型制导迫击炮弹采用的飞控模块输出结果对比曲线。图3 -51 所示为俯仰舵控角仿真测试结果, 可以看出, 飞控模块输出的俯仰舵控角和仿真计算机解算的俯仰舵控角差别非常小, 大部分时间两者重合, 但是由于两者的解算精度并不一致, 所以不能做到完全重合。图3 -52 所示为偏航舵控角仿真测试结果, 可以看出, 飞控系统输出的偏航舵控角和仿真计算机解算的偏航舵控角差别也非常小, 大部分时间两者重合。因此, 在制导律合适的情况下, 飞控模块计算特性对落点精度的影响不是主要影响。

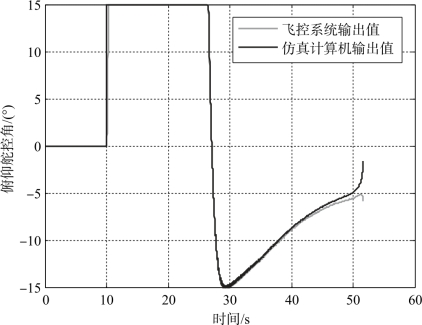
pagenumber_ebook=117,pagenumber_book=101

图3-51　俯仰舵控角仿真测试结果

pagenumber_ebook=118,pagenumber_book=102

图3-52　偏航舵控角仿真测试结果

4.地磁测姿模块特性对射击精度影响的仿真分析

地磁测姿模块利用地磁传感器感受弹丸飞行不同位置的地磁场信息, 通过对地磁场信息的解算获取弹丸飞行的滚转角和滚转角速度。

地磁测姿模块测量的滚转角不可避免地会存在误差, 有些误差是由磁阻传感器安装误差、灵敏度误差、零位误差等引起, 有些误差则是环境干扰所引起, 而地磁测姿组件的测角精度可能会对最终的射击精度产生影响。

将地磁测角误差分为均值误差和随机误差, 通过模拟打靶分析地磁测角均值误差和随机误差对射击精度的影响。将地磁测角均值误差分别设定为-10°、-8°、-6°、-4°、-2°、0°、2°、4°、6°、8°、10°, 进行模拟打靶, 得到结果如图3 -53 所示。将地磁测角标准差分别设定为1°、2°、3°、4°、5°、6°、7°、8°、9°、10°, 进行模拟打靶, 得到结果如图3 -54 所示。

从图3 -53 和图3 -54 可以看出, 地磁测角均值误差和标准差对射击精度的影响都比较小。地磁测角均值误差在10°以内时, CEP 的变化范围在0.5 m以内; 地磁测角标准差在10°以内时, CEP 的变化范围在0.6 m 以内。目前,对地磁测姿模块的测角误差一般都要求在5°以内。

虽然滚转角测量均值误差会影响舵机弹道修正能力的利用效率, 对舵机弹道修正能力造成一定的损失, 但在舵机修正能力依然能够覆盖落点散布的情况下, 滚转角测量均值误差对射击精度的影响较小。

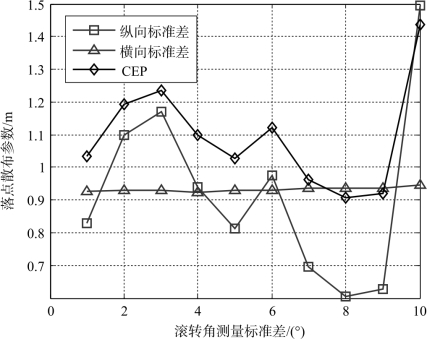
pagenumber_ebook=119,pagenumber_book=103