会计美学：数学之美-会计美学

第三节　会计理论的数学美

数学是科学家一致公认的最具有美感的一门自然科学。数学历来被人们誉为“自然科学的王冠”。

数学作为一类特殊的计算方法或者计算工具，具有普遍适用性的特点。任何一门学科，只要应用了数学思维，也就有了相应的数学美。马克思对专门学科数学化的问题也非常重视。他认为，一门学科是否达到精密化的标准，就是看这一门学科具体运用数学到什么程度^[18]。

一、数学化是最重要的科学美学标准

数学化是历史上最早从科学审美实践中总结、归纳出来的科学审美标准。从毕达哥拉斯到哥白尼、刻卜勒、普朗克和爱因斯坦，都把科学理论是否能够数学化，看做是判定其美学价值大小的一个重要标准。当然，这些自然科学的大师巨匠，也都竭力想在自己的理论研究中，闪现这种数学美的光辉。

毕达哥拉斯把数学美看做是一切事物的普遍原则;认为世界上的一切皆是“数”;宇宙的和谐是由“数”来决定的;“数”为宇宙的构造提供了一个原型;一切物体的存在方式取决于数量及其几何形状;“数”是自然物体的形状、形式和形象;人通过“数”，可以把握到人的感官不能感觉到的物体的本源;如果没有“数”和“数”的性质，那么世界上任何事物或它与别的事物之间的关系，就都不能被人清楚地了解;人们可以在一切事物上看到“数”的力量^[19]。

作为实验物理鼻祖的意大利科学家伽利略反复强调，定量的实验研究就是物理学数学化的过程;伽利略坚定地认为，没有什么学科是用不上数学的;数学应当使自己适应事物，并用来解释自然;数学证明可以用来探索牵涉可以量化的任何问题;伽利略明确表示，宇宙之书是用数学的语言写成的;没有这些数学语言和数学符号的帮助，人们就会在黑暗的迷宫中徒劳地徘徊;数学证明所提供的真知，是和神的智慧所认识到的真知是一样的^[20]。

既是物理学家，又是哲学家的马赫，更是把数学化的思维形式，提高到科学审美理想的高度来认识。马赫认为，数学方程式是最完美的;整个世界就存在于数学方程式中;数学的函数概念比因果概念更优越;他认为数学的函数概念可以避免一切不完全性、不确定性和片面性;函数关系比任何形式更接近物理世界的真实图景;函数概念对一切科学都适用，不但适用于物理学，也适用于生物学和其他学科;物质世界只不过存在于所有数学方程式中最好的一个方程式里。马赫认为，数学的效力在于它回避了所有不必要的思想，并具有免除繁复智力运算的奇特能力;数学的想象力对科学理论研究是绝对必须的^[21]。

爱因斯坦在解释为什么自然科学家那么青睐数学时说:“为什么数学比其他一切科学受到特殊的尊重，一个理由是它的命题是绝对可靠的无可争辩的，而其他一切科学的命题在某种程度上都是可争辩的，并且经常处于会被新发现的事实推翻的危险之中。……但是数学之所以有高声誉，还有另一个理由，那就是数学给予精密自然科学以某种程度的可靠性，没有数学，这些科学是达不到这种可靠性的。”^[22]

爱因斯坦认为，数学化这种思维形式，可以使客观世界的物理体系能够符合人类感觉经验的深化，而不是使人类的感觉经验僵硬地服从已经变得不那么美的原有理论框架的约定。爱因斯坦通过自己的科学研究实践认识到:优美的数学形式和现实的物理世界之间，一定有某种必然的联系。因此，爱因斯坦坚定地说:“理论科学家在他探索理论时，就不得不愈来愈听从纯粹数学的、形式的考虑，因为实验家的物理经验不能把他提高到最抽象的领域中去。”爱因斯坦是最讲究因果性的，然而他认为，“只有微分定律的形式才能完全满足近代物理学家对因果性的要求”^[23]。

量子力学的创始者、诺贝尔奖获得者玻尔认为，在研究量子力学的过程中，正是遵循了数学化的思维形式，才取得可喜的成果。他从自己的研究过程中总结出这样一条经验:“数学符号的广泛应用是量子力学方法的特点，这种应用使我们很难撇开数学细节而对这些方法的优美性及逻辑无矛盾性提供一个真实的印象。”^[24]量子力学的发展史也告诉我们:量子力学的问题，一旦和合适的数学思维形式结合，就立刻可以得到一种非常优美的形式。因为数学思维形式，恰好可以弥补我们的形象思维能力在微观世界中的局限性。在洞悉微观世界美的王国的征途中，数学化始终是照亮崎岖山路的明灯，因为它为科学家提供了进一步开辟通路的思想工具。

玻尔继承了毕达哥拉斯关于数的和谐的理论观点，他认为:“自然科学家长期以来最大胆的梦想之一就是:根据纯数的考虑来建立对于自然规律的理解。”^[25]玻尔对数学思维有很高的评价。他强调指出:“数学符号和数学运算定义，是以普通语言的简单逻辑应用为基础的。因此，数学不应被看成以经验积累为基础的一个特殊的知识分支，而应被看成普通语言的一种精确化，它用表示关系的适当工具补充了普通的语言，对于这些关系来说，通常的字句表达是不准确的或太纠缠的。”^[26]

如果说毕达哥拉斯对数学形式的美，还只是天才的猜测的话，那么经过16～20世纪这400年间所有自然科学家的共同努力，数学化的思维形式已经成为近代科学家进行科学研究必不可少的思维形式了。

二、数学化的审美含义

数学思维形式，在其历史演变的过程中，逐渐具备了以下一些特殊的含义:

第一，数学的精确性。这是数学特有的一种思维品格。因为数学是人类纯粹思维的产物，所以它可以排除现实世界中一切能够干扰结果正确性的因素，精确地获得在纯粹条件下的计算结果，从而可以为现实世界一切抽象化的理论或者理想化的模型，提供数学思维的方式。现实世界中所有的问题，只要经过数学化的处理，也就具有精确性的特点。这就是说，只要提供现实世界问题的初始条件和边界条件，那么就可以通过数学化的途径，精确地得到研究对象任何时刻的状态函数。

第二，数学的严密性。因为数学是人类纯粹思维的产物，所以它的推演、发展，只服从人类特有的思维规律——逻辑规律。逻辑规律是和自然规律、社会规律并行的3大运动规律。逻辑规律以严密性为基本特征。这就是说，逻辑规律要求人的思维结果不应该有内在的矛盾。既然数学思维遵循的是逻辑规律，那么它的理论形式当然也应该符合逻辑规律的要求。数学理论中所有定理、定律、推论、方程、公式等形式所表达的内容，或者是算符运算法则、规则等数学工具，都不应该存在内在的逻辑矛盾。

第三，数学的简单性。人类的思维规律是追求简单明了。数学思维通过数学化过程表现出来的理论论证，也必须要尽量的简单，从而达到最精炼论证的程度。长期以来，数学家们追求的理想境界，就是用最少的数学语言，表达、阐述最多的科学内容。越是简单的数学理论，它的美学价值就越高。

第四，数学的普遍性。因为数学是人类纯粹思维的产物，所以它和现实世界中一切具体的物理过程没有任何关系。这样，数学思维过程所必需的数学符号和其他用语，就可以达到高度的统一。正是这种数学符号和其他用语的高度统一，才使得数学具有普遍的适用性。任何现实世界的问题，只要能够通过数学化的过程，建立起相应的数学模型，就可以轻而易举地直接引用数学理论的成果，从而使数学思维形式和客观物质世界达到惊人的一致!

第五，数学的对称性。数学形式虽然是人类纯粹思维的产物，但是在数学形式尚处于比较低级的阶段时，它还必须依赖现实物质世界的原型进行理论思维。几何学之所以能够产生，其最初的动因就是因为印度尼罗河水的不断泛滥，冲毁了原来可以证明土地所有权的地界标志，为此必须经常重复地进行地界测量，从而促使几何学的诞生。由于现实物质世界存在着一类具有高度对称性的物质现象，因此，从这些具有高度对称性的物质现象抽象出来的数学思维产物，也就具有数学形式的对称性。如果在数学理论中出现了对称性的形式，那就是非常漂亮的理论形式。

三、数学化对会计学发展的重要意义

在一些会计学的著作中，数学方法，特别是数学分析方法，已经得到了某种程度的应用，例如:比较分析法、比率分析法、动态分析法、因素分析法、平衡分析法、结构分析法、图表分析法、线性规划法、矩阵分析法等。这些数学方法的引入，对相关经济活动状况的研究和分析很有帮助。然而在会计师中，能够自觉运用数学思维形式来进行会计理论研究的人，确实并不太多。

众所周知，会计学和数学，起源于共同的原始思维^[27]。在原始社会，人类计量、记录思想的演进，和人类关于数的思维活动、关于数学运算的逻辑思维活动的演进是同时进行的。人类原始的计量、记录行为本身，就是一种原始的“数学”行为;而人类萌芽状态的数学思维，又和经济活动事项的计量、记录有着密切的关系。这充分说明人类会计思想(包括统计思想)的起源，与人类数学思想起源的一致性^[28]。可是经过几千年来科学的分化和发展，今天数学所达到的理论分析水平和数理逻辑的发展水平，远远超越了会计学的发展水平。今天的会计学，即使和同属于经济学一级学科的其他学科，例如计量经济学、统计学、管理学等学科相比，在数学化的道路上，也已经大大地落后了^[29]。

为什么会有这样的历史结局?

我们认为，有以下4个因素，使得会计学的数学思维形式，远远落后于数学和其他学科。

第一，人员素质不同。从古至今，从事会计工作的人，其文化水平和智力水平，都远逊于数学家。这是一个不争的事实。

在原始社会向奴隶社会过渡时期，开始出现了专门的会计人员。在神庙中，这种工作最初由祭司兼任。不久，这项工作便由祭司指定的“神庙管理人”担任了。在部落中，“会计”活动最初也是由部落首领或者其他级别比较高的人兼任，后来才逐渐成为一种专职的工作。在埃及，这种专职的计量、记录者，被称为“书记(或书吏)”^[30]。

为什么从事会计工作的人员会发生这样的变动?

原来，经过一段时期会计工作的实践后，祭司和部落首领，或者其他级别比较高的人发现，从事粮食或者其他物品的计量、记录工作，并不需要特别聪明的头脑。因为这种计量活动，完全是一种“程序化”的活动，只要有足够的工作责任心就可以了。于是，比较聪明的一流和二流的头脑，就不再从事会计方面的工作了。换句话说，从事会计方面工作的人，只能是三流以下的头脑了。

在历史发展的进程中，这些会计人员又进一步分化为两个部分:一部分会计人员形成了“官厅会计”中各级管理财务活动的政府官员;另外一部分会计人员形成了“民间会计”中的专职会计。

可是，在从原始社会向奴隶社会过渡时期，历史上出现了许多大数学家。他们被当时的人们称为“哲人”。“哲人”是当时的人们对那些社会公认的聪明人的美誉。显然，“哲人”都是当时超一流的头脑。

正因为从事数学研究的人和从事会计事务的人，在文化水平和智力水平上有很大的差异，所以投入到这两门学科中的智力劳动，就具有非常明显的质的差异。

近代科学产生以后，这种智力投入不均等的情况，在会计学和数学研究领域内，表现得越来越严重。计量经济学、统计学、管理学的学科发展，之所以能够后来居上，也是因为在计量经济学、统计学、管理学等学科领域中，有比较高质量的智力劳动投入的缘故。

尽管从事会计学实际工作的人数非常多，然而，推动学科发展的主要因素，并不在人的数量，而在于人的质量!爱因斯坦曾经说过:在解决一流的物理学问题上，1 000个二流和三流的物理学家，也顶不过一个一流的物理学家!

第二，工作性质不同。会计是事务性的工作，而数学、计量经济学、统计学、管理学等学科，都是研究性的工作。事务性工作的特点，使得绝大多数会计人员，很少再有精力去从事专门的会计学理论研究。因此，会计这种事务性工作的性质，决定了他们只能日复一日，年复一年地进行重复性的劳动。

可是数学、计量经济学、统计学、管理学等学科的研究工作，就不是什么重复性的劳动，而是创造性的劳动。这些学科的发展，需要人类创造精神的尽情发挥。因此，数学研究历来被人们认为是一种“高级的智力游戏”。

第三，工作目的不同。会计人员工作的目的是为了谋生，而数学家工作的目的是为了证明自己智力的“超群”。从事计量经济学、统计学、管理学等学科研究的科学家，其工作的目的也不是为了谋生。

会计作为一种专门的职业，是从事会计工作的人的谋生手段。会计工作完全不是会计师可以“随心所欲”地、“自由”地、充分地发挥其想象力的职业。

可是在近代大学没有产生之前，数学研究并不是一种职业。因此，有条件从事数学研究的人，必然是基本生活资料有保障的人。他们不必为自己的温饱问题担忧，也不必为了生活琐事而浪费他们的心智。因此，他们的数学研究活动，纯粹只是“为数学而数学”，“为游戏而数学”。正因为数学家没有任何生活的压力，所以他们就可以“随心所欲”地、“自由”地进行研究，可以充分地发挥其想象力。他们想研究什么，就可以研究什么;想用多少时间研究，就可以用多少时间研究。

第四，对数学美的审美观照不同。一个不可否认的事实是:数学家特别重视数学美的问题;而会计人员却相对忽视，甚至鄙视数学美的问题。

数学家在自己的研究工作中，常常为了获得或者为了享受数学的美感而废寝忘食地工作。他们会以一生的精力，去追求完美的数学形式。可是从事会计工作的人，显然不会在实际的会计实务中去积极地发现美。相反的，很多的会计师，认为美和会计没有任何关系，从而轻易地关闭了会计学通往美学的大门。

正是由于上述这四方面因素的共同作用，使得原来是同源共生的会计学和数学，走上了截然不同的发展道路。

总结历史的经验，我们认为，会计理论体系的落后，在很大的程度上，是由于会计人员对数学思维形式的淡漠，是对数学化这个最重要的会计美学思想的轻视。因此，会计理论要发展，会计人员不但应该学习数学知识，吸收更多的数学营养，而且应该要学习数学家那种对数学美的虔诚之心，承认并重视会计理论体系中数学美的问题。会计师们只有改变观念，才有发现、追求会计美的动力。

四、成本会计学中的数学思维

作为一个研究范例，我们可以具体讨论一下成本会计学理论体系的数学化问题。

成本会计学理论体系的主要目标，就是要对费用进行核算，对成本进行分析和控制。其中最重要的是合理分配费用，计算成本。

为了合理分配费用，计算成本，在成本会计学理论中，引入了很多的计算公式，可是这些公式全都是文字公式，并没有用数学形式对所有的成本现象进行抽象、概括。正如在本节开始时，我们引用物理学家玻尔批评的话语:“对于这些关系来说，通常的字句表达是不准确的或太纠缠的。”在成本会计学中，所有用普通文字表达的关系，也都产生了不准确、不精确的问题，而且这种表述也非常噜苏(就是玻尔所说的“太纠缠”)。

这不但使学习者必须用很多时间去记忆这些文字公式，而且增加了成本核算过程的错误率。

为了使读者对用通常的文字公式来表达数量关系的“纠缠性”有一个明晰的感性印象，我们将不厌其烦地把成本会计学中一些基本的文字计算公式罗列如下。

(一)烦琐的费用分配公式

1.材料费用的分配公式

(1)按重量比例分配原材料费用

某产品应分配原材料费用(数量)=该产品重量×原材料费用(数量)分配率

如果分配的结果还不是直接的原材料费用，则:

某产品应分配原材料费用=该产品分配的原材料数量×原材料单价

(2)按产品产量(产值)比例分配原材料费用

某产品应分配原材料费用(数量)=该产品产量(或产值)×原材料费用(数量)分配率

如果分配的结果还不是直接的原材料费用，则:

某产品应分配原材料费用=该产品分配的原材料数量×原材料单价

某产品标准产量=该产品实际产量×该产品产量系数

某产品应分配原材料费用(数量)=该产品标准产量×原材料费用(数量)分配率

如果分配的结果还不是直接的原材料费用，则:

某产品应分配原材料费用=该产品分配的原材料数量×原材料单价

(4)按材料定额消耗量比例分配原材料费用

某产品原材料定额消耗量=该产品产量×单位产品原材料消耗定额

某产品应分配原材料费用(数量)=该产品原材料定额消耗量×原材料费用(数量)分配率

如果分配的结果还不是直接的原材料费用，则:

某产品应分配原材料费用=该产品负担的原材料数量×原材料单价

(5)按材料定额费用比例分配原材料费用

某产品原材料费用定额=该产品该材料消耗定额×计划单价

某产品原材料定额费用=∑(该产品产量×某材料费用定额)

某产品应负担原材料费用=该产品原材料定额费用×原材料费用分配率

2.燃料费用的分配公式

(1)按重量比例分配燃料费用

某产品应分配燃料费用(数量)=该产品重量×燃料费用(数量)分配率

如果分配的结果还不是直接的原材料费用，则:

某产品应分配燃料费用=该产品分配的燃料数量×燃料单价

(2)按产品体积比例分配燃料费用

某产品应分配燃料费用(数量)=该产品体积×燃料费用(数量)分配率

如果分配的结果还不是直接的原材料费用，则:

某产品应分配燃料费用=该产品分配的燃料数量×燃料单价

(3)按所耗原材料的数量或费用所分配燃料费用

某产品应分配燃料费用(数量)=该产品所耗原材料数量×燃料费用(数量)分配率

(4)按燃料定额消耗量(数量)比例分配燃料费用

某产品燃料定额消耗量=该产品产量×单位产品燃料消耗定额

某产品应分配燃料费用(数量)=该产品燃料定额消耗量×燃料费用(数量)(分配率)

如果分配的结果还不是直接的原材料费用，则:

某产品应分配燃料费用=该产品负担的燃料数量×燃料单价

(5)按燃料定额费用比例分配燃料费用

某产品燃料费用定额=该产品燃料消耗定额×计划单价

某产品燃料定额费用=∑(该产品产量×燃料费用定额)

某产品应负担燃料费用=该产品燃料定额费用×燃料费用分配率

3.动力费用的分配

(1)按机器工时(或马力)分配动力费用

某产品应分配动力费用(数量)=该产品机器工时(或马力工时)消耗量×动力费用(数量)分配率

(2)按生产工时分配动力费用

某产品应分配动力费用(数量)=该产品机器工时(或马力工时)消耗量×动力费用(数量)分配率

(3)按定额耗用量分配动力费用

某产品动力定额消耗量=该产品产量×单位产品动力消耗定额

某产品应分配动力费用(数量)=该产品动力定额消耗量×动力费用(数量)分配率

如果分配的结果还不是直接的原材料费用，则:

某产品应分配动力费用=该产品负担的动力数量×动力单价

(4)按实际耗用的动力数量分配动力费用

某产品应分配动力费用(数量)=该产品所耗动力数量×动力费用(数量)分配率

4.集体工资分配

(1)班组集体计件工资的分配

某工人应得计件工资=该工人日工资率或小时工资率×出勤日数或工时数×班组内工资分配率

(2)多品种生产某工人的工资分配

某产品应负担的工资费用=该产品实际生产工时或定额工时×生产工人工资费用分配率

(3)奖金、津贴、补贴等的费用分配

某产品应负担的奖金、津贴、补贴等费用=该产品计件工资×奖金、津贴、补贴等分配率

5.辅助生产费用分配

(1)直接分配法

某受益单位应负担的辅助生产车间费用=该受益单位耗用量×某辅助生产车间费用分配率

(2)顺序分配法

某受益单位应负担的辅助生产车间费用=该受益单位耗用量×排第一位的辅助生产车间费用分配率

某受益单位应负担的辅助生产车间费用=该受益单位耗用量×排第二位及以后的辅助生产车间费用分配率

(3)一次交互分配法

其他辅助生产车间应负担该辅助生产车间费用=该受益单位耗用量×交互分配率

某受益单位应负担的辅助生产车间费用=该受益单位耗用量×对外分配率

(4)计划分配法

辅助生产车间以外的受益单位应负担的辅助车间生产费用差额=该受益单位耗用量×差额分配率

6.制造费用的分配

(1)按生产工人工时比例分配

某产品应负担制造费用=该产品生产工人工时(或定额工时)×制造费用分配率

(2)按生产工人工资比例分配

某产品应负担制造费用=该产品生产工人工资×制造费用分配率

(3)按机器工时比例分配

某产品应负担制造费用=该产品机器工时×制造费用分配率

(4)按实际产量计划分配率法

某产品某月应分配制造费用=该产品该月生产工人定额工资×制造费用计划分配率

(5)按生产工人定额工时计划分配率法

某产品某月应分配制造费用=该产品该月生产工人定额工时×制造费用计划分配率

(6)按生产工人定额工资计划分配率法

某产品某月应分配制造费用=该产品该月生产工人定额工资×制造费用计划分配率(www.chuimin.cn)

(7)按生产工人机器定额计划分配率法

某产品某月应分配制造费用=该产品该月机器定额工时×制造费用计划分配率

(8)年未差异调整分配率法

某产品应负担制造费用的差额=该产品全年按计划分配率分配的制造费用总额×制造费用差额分配率

7.废品应该负担的费用分配

(1)不可修复废品应该负担的原材料费用分配

废品应分配原材料费用(数量)=废品件数×原材料费用(数量)分配率

(2)不可修复废品应该负担的直接人工费用分配

废品应分配直接人工费用=废品件数×直接人工费用分配率

(3)不可修复废品应该负担的制造费用分配

废品应分配制造费用=废品件数×制造费用分配率

8.在产品成本计算法

(1)在产品成本按所耗原材料费用计算法

在产品应分配成本费用=在产品件数×在产品费用分配率

(2)在产品成本按约当产量计算

在产品某工序的约当产量=该工序在产品件数×该工序的完工率

在产品某成本项费用=月末在产品约当产量×某成本项费用分配率

完工产品某成本项费用=完工产品产量×某成本项费用分配率

(3)在产品成本按定额消耗量比例分配费用计算法

在产品某成本项目费用=月末在产品定额消耗量×消耗量分配率

完工产品某成本项目费用=完工产品定额消耗量×消耗量分配率

(4)在产品成本按所定额费用比例计算法

在产品某成本项费用=月末在产品该项定额费用×某成本项费用分配率

完工产品某成本项费用=完工产品该项定额费用×某成本项费用分配率

9.分批法在产品成本费用计算法

(1)分批法在产品原材料成本费用计算法

在产品原材料成本项费用=月末在产品约当产量×原材料成本项费用分配率

完工产品原材料成本项费用=完工产品产量×原材料成本项费用分配率

(2)分批法在产品直接人工成本费用计算法

在产品直接人工成本项费用=月末在产品约当产量×直接人工成本项费用分配率

完工产品直接人工成本项费用=完工产品产量×直接人工成本项费用分配率

(3)分批法在产品制造费用成本费用计算法

在产品制造费用成本项费用=月末在产品约当产量×制造费用成本项费用分配率

完工产品制造费用成本项费用=完工产品产量×制造费用成本项费用分配率

10.逐步分项结转分步法在产品和半成品成本费用计算法

(1)第一步骤在产品和半成品原材料成本费用计算法

第一步骤半成品应分配原材料费用(数量)=第一步骤半成品数量×原材料费用(数量)分配率

第一步骤在产品应分配原材料费用(数量)=第一步骤在产品数量×原材料费用(数量)分配率

(2)第一步骤在产品和半成品直接人工成本费用计算法

第一步骤半成品应分配直接人工费用(数量)=第一步骤半成品数量×直接人工费用(数量)分配率

第一步骤在产品应分配直接人工费用(数量)=第一步骤在产品数量×直接人工费用(数量)分配率

(3)第一步骤在产品和半成品制造费用成本计算法

第一步骤半成品应分配制造费用=第一步骤半成品数量×制造费用分配率

第一步骤在产品应分配制造费用=第一步骤在产品数量×制造费用分配率

(4)第二步骤在产品和半成品制造成本计算法

第二步骤产成品应分配直接人工费用=第二步骤产成品数量×原材料费用分配率

第二步骤在产品应分配直接人工费用=第二步骤在产品数量×原材料费用分配率

(5)第二步骤在产品和产成品直接人工成本费用计算法

第二步骤产成品应分配直接人工费用(数量)=第二步骤产成品数量×直接人工费用(数量)分配率

第二步骤在产品应分配直接人工费用(数量)=第二步骤在产品数量×直接人工费用(数量)分配率

(6)第二步骤在产品和产成品制造费用成本计算法

第二步骤产成品应分配制造费用=第二步骤产成品数量×制造费用分配率

第二步骤在产品应分配制造费用=第二步骤在产品数量×制造费用分配率

12.平行结转分步法在产品和半成品成本费用计算法

(1)平行结转分步法在产品和半成品成本原材料费用计算法

应计入产成品中原材料成本项费用份额=完工产品数量×原材料成本项费用分配率

(2)平行结转分步法在产品和半成品成本直接人工费用计算法

应计入产成品中直接人工成本项费用份额=完工产品数量×直接人工成本项费用分配率

(3)平行结转分步法在产品和半成品成本制造费用计算法

应计入产成品中制造费用成本项费用份额=完工产品数量×制造费用成本项分配率

(4)平行结转分步法在产品和半成品成本原材料定额费用计算法

应计入产成品中原材料成本项费用份额=完工产品定额材料成本×原材料成本项费用分配率

应计入广义在产品中原材料成本项费用份额=广义在产品定额材料成本×原材料成本项费用分配率

(5)平行结转分步法在产品和半成品成本直接人工定额费用计算法

应计入产成品中直接人工成本项费用份额=完工产品定额直接人工成本×直接人工成本项费用分配率

应计入广义在产品中直接人工成本项费用份额=广义在产品定额直接人工成本×直接人工成本项费用分配率

(6)平行结转分步法在产品和半成品成本制造费用定额计算法

应计入产成品中制造费用成本项费用份额=完工产品定额材料成本×制造费用成本项费用分配率

应计入广义在产品中制造费用成本项费用份额=广义在产品定额材料成本×制造费用成本项费用分配率

13.分类法计算成本方法

(1)分类法计算原材料成本方法

标准产品原材料成本项费用份额=标准产品完工产品定额成本×标准产品原材料成本项费用分配率

(2)分类法计算直接人工成本方法

标准产品直接人工成本项费用份额=标准产品完工产品定额成本×标准产品直接人工成本项费用分配率

(3)分类法计算制造费用成本方法

标准产品制造费用成本项费用份额=标准产品完工产品定额成本×标准产品制造费用成本项费用分配率

14.联产品成本计算方法

(1)联产品计算原材料成本方法

某联产品应分配原材料费用(数量)=该联产品重量×原材料费用(数量)分配率

如果分配的结果为数量，则:

某联产品应分配原材料费用=该联产品分配的原材料数量×原材料单价

(2)联产品计算直接人工成本方法

某联产品应分配直接人工费用(数量)=该联产品重量×直接人工费用(数量)分配率

如果分配的结果为数量，则:

某联产品应分配直接人工费用=该联产品分配的直接人工数量×直接人工单价

(3)联产品计算制造费用成本方法

某联产品应分配制造费用=该联产品重量×制造费用分配率

15.副产品成本计算方法

与上述联产品的成本计算方法完全相同。

副产品应分配制造费用=该副产品重量×制造费用分配率

16.等级产品成本计算方法与上述联产品的成本计算方法完全相同。

某等级产品应分配制造费用=该等级产品重量×制造费用分配率

17.定额成本计算方法

完工产品应负担的脱离定额差异额=完工产品定额成本×脱离定额差异分配率

在产品应负担的脱离定额差异额=在产品定额成本×脱离定额差异分配率

18.作业成本法分配制造费用

分解不同的作业，然后按照作业的类别计算制造费用的分配问题。

有几个作业，就用几次上述公式，然后相加求和。

此外，还有很多类似的公式，我们就不在此赘述了。

当我们认真研究这些公式后，可以发现:这些文字公式虽然很多，但是却大同小异。相信读者看了上述这些文字公式以后，没有一个人不感到厌烦和头痛的。因为我们在罗列这些公式时，心里就感到非常烦躁。这样烦琐的公式，怎么会使学生有学习的兴趣呢?

读这些公式，完全可以用“味同嚼蜡”这个词来形容。在这些文字公式中，我们感受到美吗?没有，根本没有!然而，当我们翻开任何一本成本会计学的课本，映入眼帘的，尽是这些没有任何美感的文字表达公式!

成本会计学的教科书是这样，其他会计学的教科书基本上也是这样。读者(学生)的痛苦，是完全可以想象得到的。

这就是轻视数学化思维形式的必然结果!

能不能把数学思维的形式引进成本会计学的学科体系，通过数学化的途径，对这些毫无美感的文字公式彻底加以改造呢?

当然可以!

(二)对成本会计学文字公式的数学化改造

我们现在对上述文字公式进行数学化的改造。

式中Ma_i——第i个成本计算对象应该负担的费用;

a_i——第i个成本计算对象的分配标准;

Md——待分配的总费用;

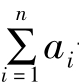——n个成本计算对象统一的分配标准之和。

有了这个普遍适用的费用分配的数学公式，就可以概括前述所有近百个文字公式。我们(学生)只要理解这个普遍适用的费用分配公式在不同条件下的会计意义，就可以轻易地解决所有的费用分配问题。

下面我们举几个具体例子加以说明。读者完全可以举一反三地领会。

1.计算原材料的费用分配

当:

Md为待分配的原材料费用的总额;

a_i为第i个产品(成本计算对象)的分配标准(重量、体积、定额、工时等);

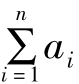为全部i个产品(成本计算对象)统一的分配标准的总和(重量、体积、定额、工时等)，

那么:Ma_i为第i个产品应该负担的原材料费用。

2.计算制造费用的分配

当:

Md为待分配的制造费用总额;

a_i为第i个产品(成本计算对象)的分配标准(机器工时、工资、定额、人工工时等);

为所有的i个产品(成本计算对象)统一的分配标准的总和(机器工时、工资、定额、人工工时等)，

那么:Ma_i为第i个产品应该负担的制造费用。

用原来教科书中的文字公式，需要经过2个或2个以上的步骤才能计算出一个成本费用的分配值，现在只要用一个公式就可以解决问题了^[31]。

(三)费用分配数学公式的推论

我们还可以对这个费用分配的数学公式作进一步的推论:

推论一:在会计学的理论体系中，只要涉及费用的分配问题，就一定可以用这个公式进行费用的分配。

推论二:即使不是会计学的理论体系，只要涉及费用或者其他物资的分配问题，也一定可以用这个公式进行费用或者物资的分配。

有了这个普遍适用的费用分配的数学公式，结果是多么的简单!应该说这是会计学中一个非常漂亮的公式。

其实，我们在成本会计学的教学过程中总结出来的这个普遍适用的费用分配的数学公式，只是最简单的数学思维的运用，得出的结果却是如此的赏心悦目!仅此一点，在会计学的学科体系中，难道不应该大力提倡数学思维形式吗?

由此可知，在会计学的学科体系中，显然应该有会计美学的一席之地!