【摘要】:关联规则挖掘及算法郑继刚杨春华曾庆红赵若男摘要:关联规则可分为布尔型和数值型、单层和多层、单维和多维关联规则挖掘。本文阐述关联规则的定义以及分类,详细介绍经典的关联规则挖掘Apriori算法。可信度是对关联规则准确性的衡量,是得出关联规则的依据。
关联规则挖掘及算法
郑继刚 杨春华 曾庆红 赵若男
摘 要:关联规则可分为布尔型和数值型、单层和多层、单维和多维关联规则挖掘。产生候选频繁项集的Apriori算法,首先从事务数据库中挖掘出频繁项集,然后根据频繁项集产生强关联规则。为找频繁项集,Apriori算法需要多次扫描数据库,而且可能产生庞大的候选集,这两个性能瓶颈是该算法的致命缺点,后来提出各种技术来优化Apriori算法。
关键词:数据挖掘关联规则频繁项集优化
关联规则挖掘是数据挖掘中一个重要的研究方向,用以发现事务数据库中项集间的一些内在关联或相关联系。一个典型应用是购物篮分析,顾客会在一次购物中同时购买哪些商品,得出答案后可以为决策者提供帮助。本文阐述关联规则的定义以及分类,详细介绍经典的关联规则挖掘Apriori算法。
一、关联规则概述
R.Agrawal、R. Imielinski和Swami在1993年提出了关联规则挖掘的相关概念,是数据挖掘领域一个重要的研究内容。所谓关联规则,就是发现描述数据库中数据项之间潜在的关联,找出大量数据之间未知的、有用的依赖关系。超市中使用条形码扫描器收集了大量交易数据,每条交易记录都详细地列出了购物交易中的所有信息,关联规则的产生就是源于分析这些顾客交易数据。经营者们感兴趣的是哪些商品总是被一起买走,根据这些信息使卖场布局更合理,合理编排商品分类,以及通过购买类型确定顾客类型、实施促销活动等。
定义1:设I={I1,I2,…,Im}是数据项的集合,D是全体事务的集合,一个事务T有一个唯一的标识TID。如果项集A≤T,则称事务T支持(Support)项集A,也称事务T包含项集A。
定义2:关联规则是形如A→B的蕴含式,其中A>I,B>I,且A∩B=Φ。
关联规则A→B的支持度定义为: sup port(A→B)=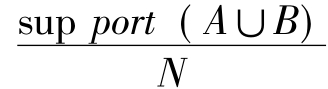 ×100%,可信度定义为: confidence(A→B)=
×100%,可信度定义为: confidence(A→B)= ×100%。
×100%。
支持度是对关联规则重要性的衡量,说明了这条关联规则在所有事务中出现的概率,支持度越大,关联规则越重要。可信度是对关联规则准确性的衡量,是得出关联规则的依据。
定义3:支持度和置信度均需大于用户设定的阈值(即最小支持度阈值和最小置信度阈值),即: sup port(A→B)≥min_ sup、confidence(A→B)≥min_ conf的关联规则称为强规则,否则称为弱规则,强关联规则是研究者所追求的有用的规则。
下表是一个超市购物篮事务例子,表中每一行对应一个事务,包含一个唯一标识符TID和顾客购买的商品集合。
表1 购物篮事务
采用Apriori算法,挖掘得到如下规则:
{尿布}→{啤酒}
[sup port=1%,confidence=30%],
该规则的支持度sup port=1%表明所有的顾客中有1%的同时购买尿布和啤酒,可信度confidence= 30%表明购买尿布的顾客当中有30%的也购买啤酒。通过发现的关联规则帮助决策者进行商品目录的设计、发现新的交叉营销机会或制定其他有关的商业决策。
二、关联规则的分类
按照不同的标准,关联规则可以分为单维的和多维的、单层的和多层的、布尔型的和数值型的等。
基于规则中处理变量的类别,关联规则可以分为布尔型和数值型。布尔型关联规则处理的值都是离散的、种类化的,它显示了这些变量之间的关系;而数值型关联规则可以和多维关联或多层关联规则结合起来,对数值型字段进行处理,将其进行动态的分割,或者直接对原始的数据进行处理,当然数值型关联规则中也可以包含种类变量。例如:性别=“女”=>职业=“秘书”,是布尔型关联规则;性别=“女”=>收入= 3 000,涉及的收入是数值类型,所以是一个数值型关联规则。
基于规则中数据的抽象层次,关联规则可以分为单层关联规则和多层关联规则。在单层关联规则中,所有的变量都没有考虑到现实的数据是具有多个不同的层次;而在多层关联规则中,对数据的多层性已经进行了充分的考虑。例如: IBM台式机=>Sony打印机,是一个细节数据上的单层关联规则;台式机=>Sony打印机,是一个较高层次和细节层次之间的多层关联规则。
基于规则中涉及的数据维数,关联规则可以分为单维的和多维的。在单维关联规则中,我们只涉及数据的一个维,如用户购买的物品,而在多维关联规则中,要处理的数据将会涉及多个维。换成另一种解释,单维关联规则是处理单个属性中的一些关系,多维关联规则是处理各个属性之间的某些关系。例如:啤酒=>尿布,这条规则只涉及用户购买的物品;性别=“女”=>职业=“秘书”,这条规则就涉及两个字段的信息,是两个维上的一条关联规则。
三、Apriori算法
对关联规则算法的研究先后出现了Apriori、FP-growth等经典算法以及基于它们的各种各样的改进算法,可分为产生候选频繁项集和不产生候选频繁项集两类。
产生候选频繁项集类:对候选频繁项集进行剪枝,采用多次对数据库自底向顶或自顶向底搜索的策略。其思想是及早尽量多地剔除实际不可能产生频繁项集的候选频繁项集,减少分析判别和运算的次数。这类算法主要有Apriori算法及其基于Apriori算法的改进算法。
不产生候选频繁项集类:将数据库投影到一棵频繁模式树上,仍保留项目集的关联信息,然后通过扫描该树中路径节点的计数来搜索频繁项集。这类算法以FP-growth算法为代表。
(一)算法描述
Apriori算法是R.Agrawal和R.Srikant在1994年提出的专为挖掘布尔型关联规则所需频繁项集的原创性算法,算法名字是缘于使用了频繁项集的性质这一先验知识。
定义4:频繁项集(Frequent Itemset,FIs)是在事务数据库中出现的次数大于或等于最小支持度阈值的项集。
算法首先找出所有的频繁项集,然后由频繁项集产生强关联规则:第一步,从事务数据库D中找出所有支持度不小于用户指定的最小支持度阈值(min_ sup)的频繁项目集;第二步,使用频繁项目集产生所期望的关联规则,产生关联规则的基本原则是置信度必须不小于用户指定的最小置信度总阈值(min_ conf)。由于第二步较为容易和直观,因此第一步挖掘出所有频繁项目集是该算法的核心,占据整个计算量的大部分,故有时仅考虑挖掘频繁项集的效率。
该算法利用了如下两个基本性质:
性质1:任何频繁项集的子集必定是频繁项集;
性质2:任何非频繁项集的超集必定是非频繁项集。算法具体描述如下:
输入:事务数据库D以及最小支持度min_ sup。
输出: D中频繁项集L。
算法: L1=寻找频繁1项集(D); For k=2; Lk-1≠Φ; k++
{ Ck= apriori_ gen(Lk-1);
For每个事务t∈D
{ Ct= subset(Ck,t);
For每个候选c∈Ct c. count++;
}(www.chuimin.cn)
Lk=(c∈Ck| c. count≥min_ sup)
}
Return L={所有的Lk}。
其中apriori_ gen是Apriori算法中的关键步骤,根据Lk-1寻找Lk,需做两个动作:连接与剪枝。连接步:通过连接产生Ck;剪枝步:如果一个候选k项集的(k-1)项子集不在(k-1)的频繁项集中,则该候选集也不可能是频繁的,从而由Ck删除。
apriori_ gen描述如下:
apriori_ gen(Lk-1: frequent(k-1)项集)
For each项集l1∈Lk-1
For each项集l2∈Lk-1
If(l1[1]= l2[1])∧…∧(l1[k-2]= l2[k-2])∧(l1[k-1]<l2[k-1])
Then
{c= l1 l2;
If has_ infrequent_ subset(c,Lk-1)
Then delete;
Else add c to Ck;
}
Return Ck。
连接步中,为找Lk,通过Lk-1与自身连接产生候选k项集的集合,将该候选项集的集合记作Ck。设l1和l2是Lk-1中的项集,记号l1[j]表示l1的第j项。执行连接Lk-1和Lk-1,其中Lk-1的元素是可连接,如果它们前(k-2)个项相同而且第(k-2)项不同,即:
l1[1]= l2[1]∧l1[2]= l2[2]∧…∧l1[k-2]= l2[k-2]∧l1[k-1]<l2[k-1]
则Lk-1的元素l1和l2是可连接的,连接l1和l2产生的结果的项集是l1[1]l1[2]…l1[k-1]l2[k-1]。
剪枝步中,Ck是Lk的超集,即它的成员可以是也可以不是频繁的,但所有的频繁k项集都包含在Ck中。扫描数据库一次,确定Ck中每个候选的计数,从而确定Lk。然而,Ck可能很大,这样所涉及的计算量就很大。为压缩Ck,可以使用任何非频繁的(k-1)项集都不可能是频繁k项集的子集这一Apriori性质。因此,如果一个候选k项集的(k-1)子集不在Lk-1中,则该候选也不可能是频繁的,从而可以从Ck中剔除。
在实际运用中有一点需要注意,那就是Apriori的候选产生检查方法大幅度压缩了候选项集的大小,并有很好的性能。
(二)算法的性能瓶颈
由生成频繁项集的过程可知,Apriori算法有两个致命的性能瓶颈:
(1)多次扫描事务数据库,需要很大的I/O负载。对每次k循环,候选集Ck中的每个元素都必须通过扫描数据库一次来验证其是否加入Lk。假如有一个频繁项集包含10个项的话,那么就至少需要扫描事务数据库10遍。
(2)可能产生庞大的候选集。由Lk-1产生k候选集Ck是指数增长的,例如104个频繁1项集就有可能产生接近107个元素的候选2项集,以此类推,为发现长度为100的频繁模式{a1,a2,…,a100},则需产生多达约1 030个候选集。如此庞大的候选集对时间开销和内存空间都是一种挑战。
由此可知,Apriori算法多次扫描事务数据库,产生庞大的候选集,让计算机在输入、输出系统上花费很多时间,频繁进出内存,需要很大的内存空间,如何减少消耗计算机资源是研究者正在探索的课题。
(三)算法的优化
在找频繁1项集、2项集、……、k项集时,每挖掘一层Lk,都要扫描整个事务数据库D一遍,第k次扫描时,得到k项集,这个扫描是重复的工作。当事务数据库D较大时,Apriori算法在时间上的开销比较大,会呈现出数量级的增加,为降低系统的输入、输出时间,研究者开始寻求一种能减少系统输入、输出时间开销的更为快捷的算法。
对Apriori算法的优化方法有分区技术、散列(Hash)技术、抽样技术、减少事务的个数、减少数据库的扫描遍数等方法。
(1)分区技术。1995年Savaser等人设计了一个基于数据分割的频繁项目集生成算法。这个算法的基本思想:首先把数据库从逻辑上分成几个互不相交的块,每次单独考虑一个分块,然后在每个数据块里讨论频繁项目集的发现问题,最后通过局部的频繁项目集得到最终的全局频繁项目集。这种方法只需要把所处理的分块放入内存,合理利用内存空间,减轻了内存需求。由于每个分块的局部频繁项目集是相对独立的,因此可以把局部频繁项目集的生产工作由不同的处理器来完成,提供了算法的并行处理机制。由于分块后的数据量急剧减少,所以该算法处理的效率就会得到较大的提高。
(2)散列(Hash)技术。1995年Park等人提出了一个产生频繁项目集的算法,该算法以散列技术为基础。通过实验发现寻找频繁项目集的主要时间开销花费在生成频繁项目集L2上,因此,Park等人利用了这个性质,在产生L2频繁项目集时引入Hash技术来进行改进。首先把需要扫描的项目集分别放到不同的Hash桶中,但是每对项目最多只可能在一个特定的Hash桶中;然后就可以对每个桶中的项目子集进行测试,这样就减少了候选项目集生成的代价。当然也可以扩展到任何的频繁项目集Lk生成上。
(3)抽样技术。1996年Toivonen提出了一种新的产生频繁项目集算法,该算法是以抽样技术为基础的。首先使用数据库的抽样数据产生一些可能成立的规则,然后利用数据库的剩余数据来验证所产生的关联规则的正确性。Toivonen提出的基于抽样的关联规则挖掘算法不仅相当简单,而且还可以显著地降低系统I/O所付出的时间开销。但是,该算法存在的最大问题是抽样数据的选取以及由此而产生的结果偏差过大,也就是所谓的数据扭曲。当然,后来也有人提出了反扭曲技术,可以改善数据扭曲问题。
(4)减少事务的个数。这种方法的基本原理是:当一个事务不包含长度为k的项目集时,则必然不包含长度为(k+ 1)的频繁项目集。因此,可以将这些事务删除掉,而在下一遍的扫描中使用减少了数据个数的事务集,故挖掘的执行效率就得到了提高。
(5)减少数据库的扫描遍数。1997年Brin等人提出了一个减少数据库扫描遍数的算法。具体的实现原理是在计算k项目集时,如果我们发现某个(k+ 1)项目集可能是频繁项目集时,我们就同时也要计算这个(k+ 1)项目集的支持度。该算法需要总的数据库扫描次数一般少于最大频繁项目集的项数,实验表明该算法比使用Apriori算法对数据库的扫描遍数要少,也比使用基于抽样算法所使用的候选集要少。
(6)并行挖掘技术。充分利用数据库的分布技术对数据库子集进行挖掘,而且各子集间可以进行并行挖掘。另外,并行挖掘技术还要涉及并行挖掘模型和算法的开发工作。
这些都是关联规则挖掘中的一些用来改善算法的优化方法,为人们改善已有算法提供了许多比较好的思路。
参考文献:
[1]Jiawei Han,Micheline Kamber.数据挖掘概念与技术[M].北京:机械工业出版社,2007.
[2]毛国君.数据挖掘技术与关联规则挖掘算法研究[D].北京:北京工业大学,2003.
[3]李雪斌,朱艳琴,罗喜召.关联规则挖掘中Apriori算法的研究与改进[J].电脑知识与技术,2009,5(19).

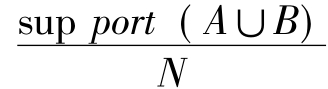 ×100%,可信度定义为: confidence(A→B)=
×100%,可信度定义为: confidence(A→B)= ×100%。
×100%。



相关推荐