决策方法：头脑风暴法和盈亏平衡点法

4.4　决策方法

4.4.1　定性决策方法

定性决策方法，是指决策者根据所掌握的信息，通过对事物运动规律的分析，在把握事物内在本质联系基础上进行决策的方法。定性决策方法主要有:

1.头脑风暴法

头脑风暴法(简称BS法)也叫思维共振法，最早是由英国的奥斯本提出的。这种方法是通过有关专家之间的信息交流，引起思维共振，产生组合效应，从而导致创造性思维的连锁反应。

用该法进行决策或预测，必须遵守以下原则:(1)严格限制决策或预测对象范围，明确具体要求。(2)不能对别人意见提出怀疑和批评，要认真研究任何一种设想，而不管其表面看来多么不可行。(3)鼓励专家对已提出的方案进行补充、修正或综合。(4)解除与会者顾虑，创造自由发表意见而不受约束的气氛。(5)提倡简短精练的发言尽量减少详述。(6)与会专家不能宣读事先准备好的发言稿。(7)与会专家人数一般为10—25人，会议时间一般为20—60分钟。

头脑风暴法一般分为以下三个阶段:第一阶段，是对已提出的每一种设想进行质疑，并在质疑中产生新设想，同时着重研究有碍于实现设想的问题。第二阶段，是对每一种设想编制一个评价意见一览表，同时编制一个可行性设想一览表。第三阶段，是对质疑过程中所提意见进行总结，以便形成一组对解决所论及问题的最终设想。实践证明，头脑风暴法可以排除折中方案，对所决策的问题通过客观分析可找到一组切实可行的方案。

2.哥顿法

哥顿法是美国人哥顿于1964年提出的决策方法。该法与头脑风暴法相类似，由会议主持人先把决策问题向会议成员做笼统的介绍，然后由会议成员(即专家成员)海阔天空地讨论解决方案;当会议进行到适当时机，决策者将决策的具体问题展示给小组成员，使小组成员的讨论进一步深化，最后由决策者吸收讨论结果进行决策。采用该方法时应选择有丰富经验的主持人，他要能很好地把握“包袱”抖搂的时机。

4.4.2　定量决策方法

定量决策方法是利用数学模型进行优选决策方案的决策方法。根据数学模型涉及的决策问题的性质(或者说根据所选方案结果的可靠性)不同，定量决策方法一般分为确定型决策、风险型决策和不确定型决策三类。

1.确定型决策方法

确定型决策方法的特点是只要满足数学模型的前提条件，决策方案就肯定会出现模型给出的特定的结果。属于确定型决策方法的模型很多，下面主要介绍两种常用的方法:盈亏平衡点法、经济批量法。

(1)盈亏平衡点法。盈亏平衡点法(也称量本利分析法)是进行产量(或销量)决策常用的方法。该方法基本特点是把成本分为固定成本和可变成本两部分，然后与总收益进行对比以确定盈亏平衡时的产量或某一盈利水平的产量。其中可变成本与总收益为产量的函数，当可变成本、总收益与产量为线性关系时，总收益、总成本和产量的关系如图4－2所示。

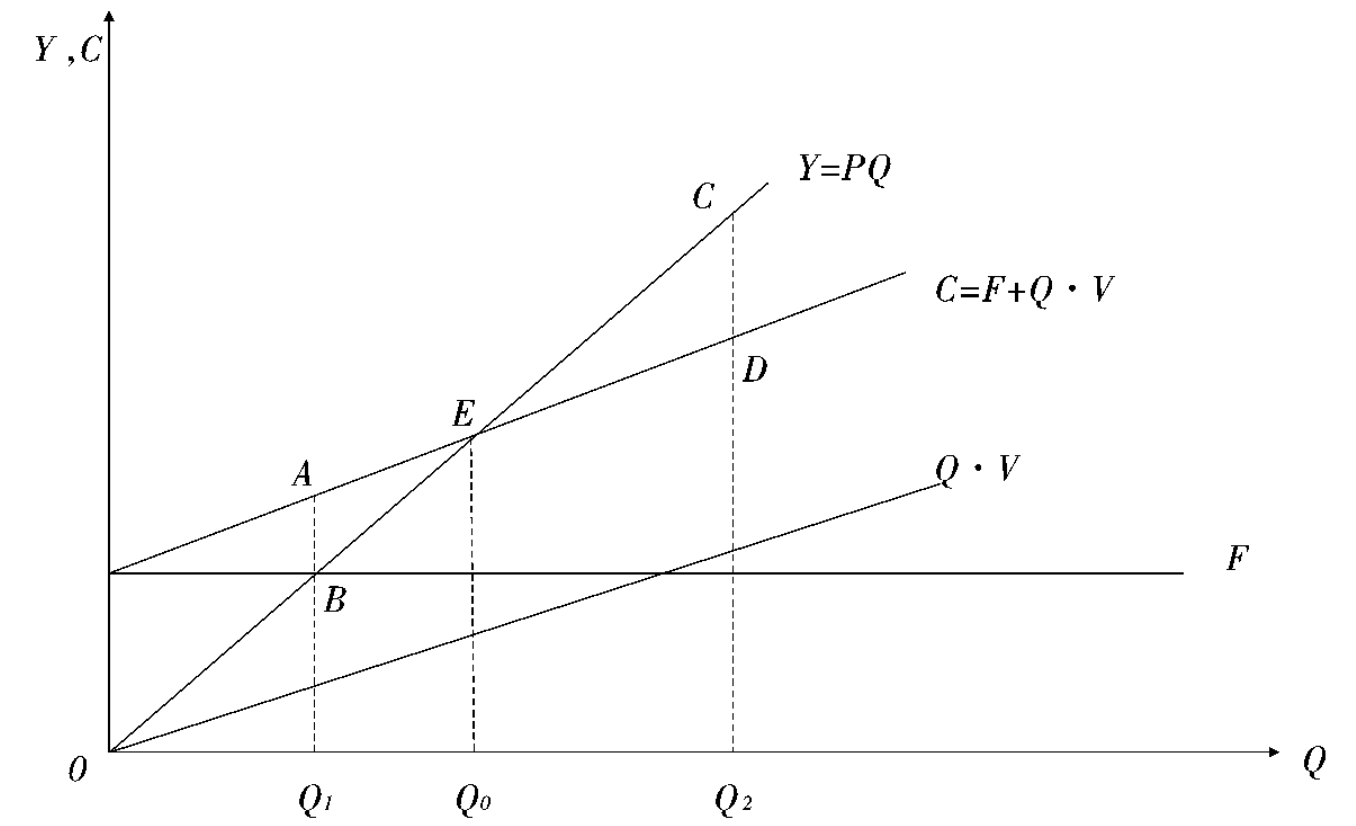
图4－2　盈亏平衡点分析示意图

图4－2中，纵坐标表示总收益(Y)、总成本(C)、固定成本(F)及可变总成本(Q·V)。横坐标表示产量(或销量，用Q表示，该模型假定产销量一致)。总收益Y是单位销售价格P与产量Q的乘积;总成本C等于固定成本F加上可变成本Q·V。总收益曲线Y与总成本曲线C的交点E对应的产量Q₀就是总收益等于总成本(即盈亏平衡)时的产量，E点就是盈亏平衡点。在E的左边，即Q＜Q₀，总成本曲线位于总收益曲线之上，即亏损区域，其中C与Y之间的纵坐标距离就是相应产量下的亏损额，如Q₁处的亏损额为AB。在E点的右边，即Q＞Q₀，总收益线位于总成本之上，即盈利区域，Y与C之间的垂直距离就是相应产量下的盈利额。如Q₂对应的盈利额为CD。

用盈亏平衡点法进行产量决策时应以Q₀为最低点，因为低于该产量就会产生亏损。对新方案的选择是如此，对于现有的生产能力是否在Q时就一定要停产呢?由上图可知，停产时的亏损额为F，即固定成本支出，而在OQ₀区间内的任一点的亏损额(C－Y)都低于F。所以企业生产能力形成后，即使受市场销量的约束使产量进入亏损区，也不应作出停产决策，即“两害相权取其轻”。

上图所示盈亏平衡点基本原理也可由公式来表示。由于在Q₀点有Y=C，即:

PQ₀=F+Q₀·V

故盈亏平衡点(或称保本点)产量

公式(4－1)中有四个变量，给定任何三个便可求出另外一个变量的值。

例:某企业生产某产品的固定成本为4万元，单位可变成本为240元，产品单位售价为250元，其盈亏平衡点的产量为:

Q₀=F/(P－V)=40000÷(250－240)=4000

该模型除了用于盈亏平衡点的产量、成本决策外，再增加一利润变量，便扩展为任意产量决策的模型。设利润为B，根据定义有:

B=PQ－(F+Q·V)

故保利点产量为:

公式(4－2)中共五个变量，给定任意四个便可求出另外一个变量的值。

例:某企业生产某产品的固定成本为4万元，单位售价250元，每单位可变成本240元，若企业目标利润为20万元，问企业应完成多少产量?

解:由公式(4－2)可得:

Q=(F+B)/(P－V)　　　　　　　　　

=(40000+200000)/(250－240)=24000

使用盈亏平衡点法决策时应注意的问题:首先，应考虑产量适用区间。按上述假定，成本中的固定成本与产量无关，显然，该假定只能在一定的产量区间内有效，当产量超过了现有生产能力并导致规模扩张时，原来的固定成本假定不再成立。其次，是总收益与可变成本和产量之间的线性关系假设。只有在线性假设下，各变量之间才有上述(4－1)式和(4－2)式关系。当出现产量的非线性收益或成本时(如因市场约束和价格折扣而产生的价格随销量的增加而下降，因扩大规模产生的单位可变成本随产量增加而下降等)，仍可由“总收益=总成本”求解盈亏平衡点产量，也可由“利润=总收益－总成本”求解利润量或目标利润下的产量，但不能再直接套用上述(4－1)和(4－2)式。

(2)经济批量法。经济活动经常遇到这样的情形:在特定时期和指定业务量条件下，每次业务量和从事该业务的次数成反比。业务活动费用有两种:一种费用由每次活动业务量的大小决定并与之成正比;另一种费用则与该种业务发生次数多少有关且与之成正比。由于每次业务量与业务发生次数的反比关系，总费用中的两个组成部分亦呈反比关系，此高彼低，总费用的最低点应如何确定?这就是最优经济批量模型所要解决的问题。

一个组织(尤其是企业)在一定时期总要耗费一定物质资料。单次订购量大时，库存费用就要增加。库存费用不仅包括仓储费用，而且还包括库存物资占用资金的利息损失。但当单次订购量大时，订货次数减少，订货费用就会降低。订货费用由寻找客户、与客户谈判、签订供货合同等费用构成，这些费用支出主要与订货次数有关。

设一单位一定时期(一年)所需某种物资数量为A，每次订购量为Q，且订货为均匀消耗;每次订货费用为K，库存费用率(即单位数量的物资的年库存费用)为C，则订货次数为A/Q，总订货费用为AK/Q，由于均匀消耗假设年平均库存量为Q/2，年库存费用为QC/2，总费用(S)由两种费用之和构成，即:

S=(A/Q)·K+(Q/2)·C

S对Q求导并使之等于0，便可求出总费用S最低时的经济订货量Q₀:

最优经济批量的图示分析见图4－3。

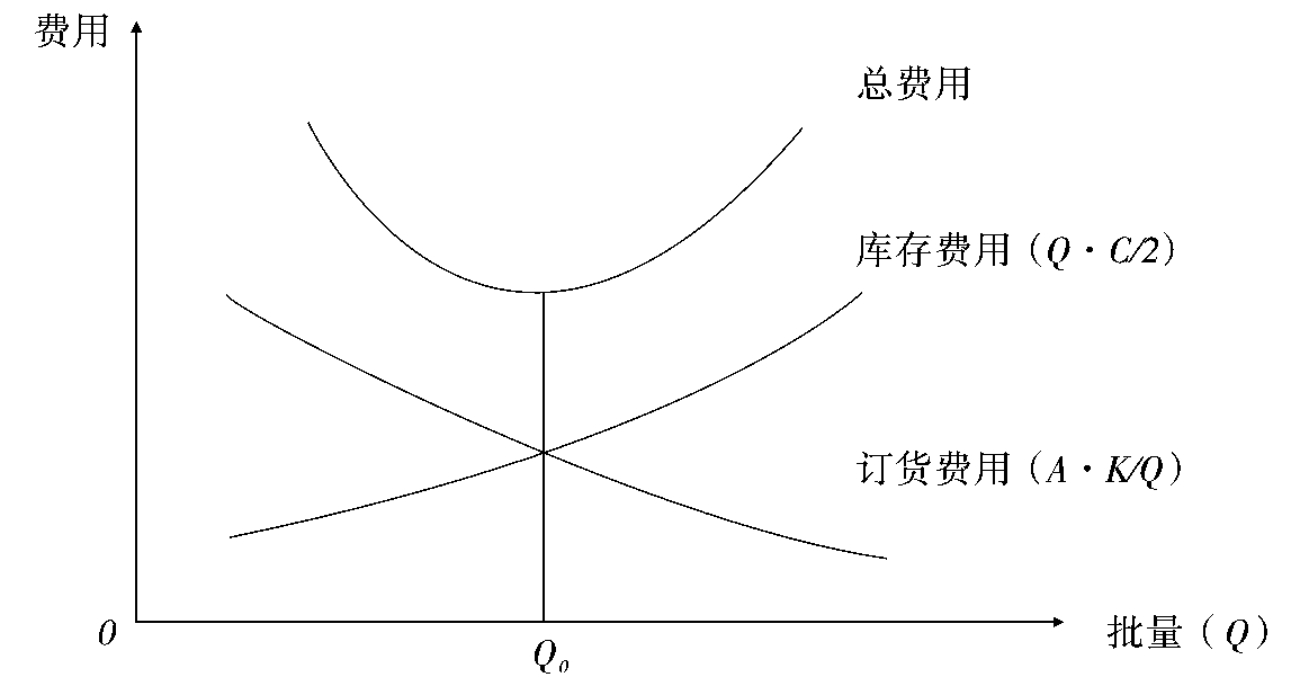
图4－3　最优经济批量图

2.风险型决策方法

当一个决策方案对应两个或两个以上相互排斥的可能状态，每一种状态都以一定的可能性出现，并对应特定的结果，这种已知方案的各种可能状态及其发生的可能性大小的决策称为风险型决策。数学上用概率来量化某一随机事件发生的可能性，即决策方案对应的某种状态的可能性大小可用概率来描述。

风险型决策的标准是期望值。所谓期望值，实质上是各种状态下加权性质的平均值。当决策指标为收益时应选取期望值最大的方案;当决策指标为成本时应选取期望值最小的方案。一个方案的期望值是该方案在各种可能状态下的损益值与其对应的概率的乘积的和。用期望值决策既可用表格表示，也可用树状图表示，后者称为决策树法。下面以决策树为例说明风险型决策方法的应用。

决策树是由决策点、方案枝、机会点、概率枝和期望值五个要素组成的树状图，如图4－4所示。它以决策结点为出发点，引出若干方案枝;每个方案枝的末端是一个状态结点，状态结点后引出若干概率枝，每一概率枝代表一种状态，每一概率枝的末端是该自然状态下的期望值。这样自左而右层层展开便得到形如树状的决策树。

决策树法的决策程序如下:

(1)绘制树形图。图形自左而右层层展开，根据已知条件排列出各方案和每一方案的各种自然状态。

(2)将各自然状态的概率标于概率枝上，并将各自然状态的期望值标于相应的概率枝后。

图4－4　决策树基本构成示意图

(3)计算各方案的期望值，并将其标于该方案对应的状态结点上。

(4)进行剪枝。比较各方案期望值，将期望值小的(即劣等方案)剪掉，用//标于方案枝上。

(5)剪枝后所剩的最后方案即为最佳方案。

例:某企业为了扩大某产品的生产，拟建设新厂。据市场预测，产品销路好的概率为0.7，销路差的概率为0.3。有三种方案可供企业选择:

方案1:新建大厂，需投资300万元。据初步估计，销路好时，每年可获利100万元;销路差时，每年亏损20万元。服务期为10年。

图4－5　决策树示意图

方案2:新建小厂，需投资140万元。销路好时，每年可获利40万元;销路差时，每年仍可获利30万元。服务期为10年。

方案3:先建小厂，三年后销路好时再扩建，需追加投资200万元，服务期为7年，估计每年获利95万元。问哪种方案最好?

画出该问题的决策树，如图4－5所示。

图4－5中，有两种自然状态:销路好和销路差，自然状态后面的数字表示该种自然状态出现的概率。位于状态枝末端的是各种方案在不同自然状态下的收益或损失。据此可以算出各种方案的期望收益。

方案1(结点①)的期望收益为:［0.7×100+0.3×(－20)］×10－300=340(万元)(www.chuimin.cn)

方案2(结点②)的期望收益为:(0.7×40+0.3×30)×10－140=230(万元)

至于方案3，由于结点④的期望收益465(=95×7－200)万元大于结点⑤的期望收益280(=40×7)万元，所以销路好时，扩建比不扩建好。方案3(结点③)的期望收益为:(0.7×40×3+0.7×465+0.3×30×10)－140=359.5(万元)

计算结果表明，在三种方案中，方案3最好。

需要说明的是，在上面的计算过程中，我们没有考虑货币的时间价值，这是为了使问题简化。但在实际中，多阶段决策通常要考虑货币的时间价值。

3.不确定型决策方法

在风险型决策中，概率是计算期望值的必要条件，因而也是按期望值标准进行方案选择的必要条件。但在现实经济活动中经常很难知道某种状态发生的客观概率，因此也无法根据期望值标准进行方案选择。这时如何进行方案选择主要依赖于决策者对待风险的态度。

(1)冒险法(大中取大法或称乐观准则)

冒险法指愿承担风险的决策者在方案取舍时以各方案在各种状态下的最大损益值为标准(即假定各方案最有利的状态发生)，在各方案的最大损益值中取最大者对应的方案。

例:某企业拟开发新产品，有三种设计方案可供选择。有关资料见表4－2。

表4－2　冒险法决策

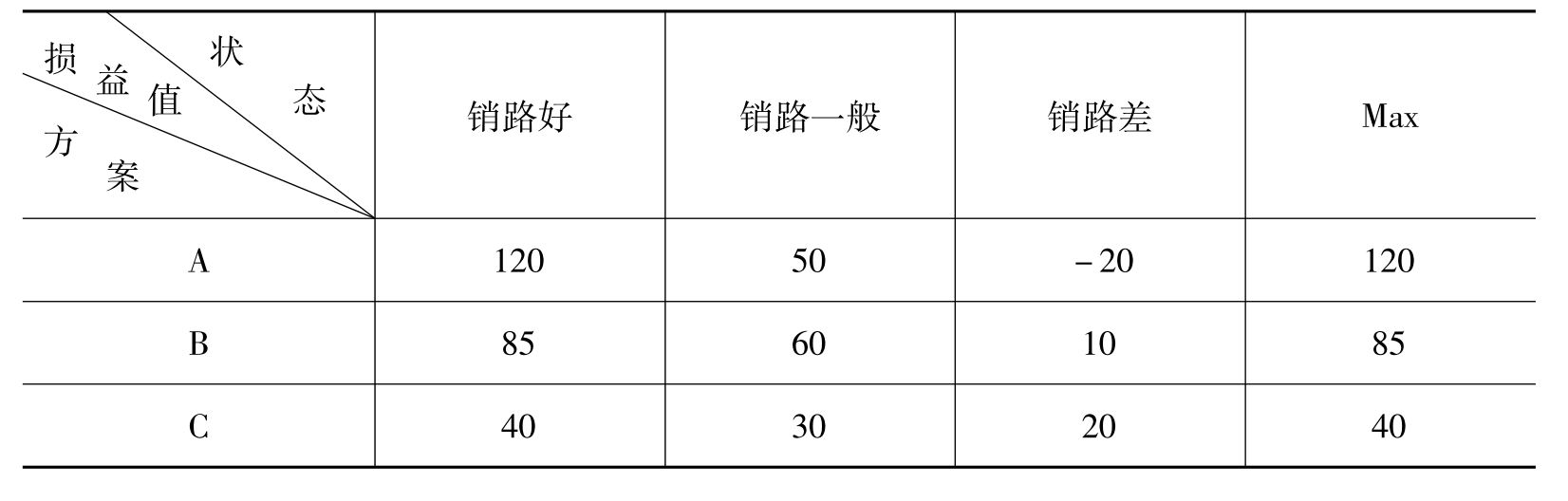
在不知道各种状态的概率时，用冒险法选择方案过程如下:

首先，在各方案的损益中找出最大者。

其次，在所有方案的最大损益值中找最大者，即max{120，85，40}=120，它所对应的方案A就是用该法选出的方案。

(2)保守法(小中取大法或称悲观准则)

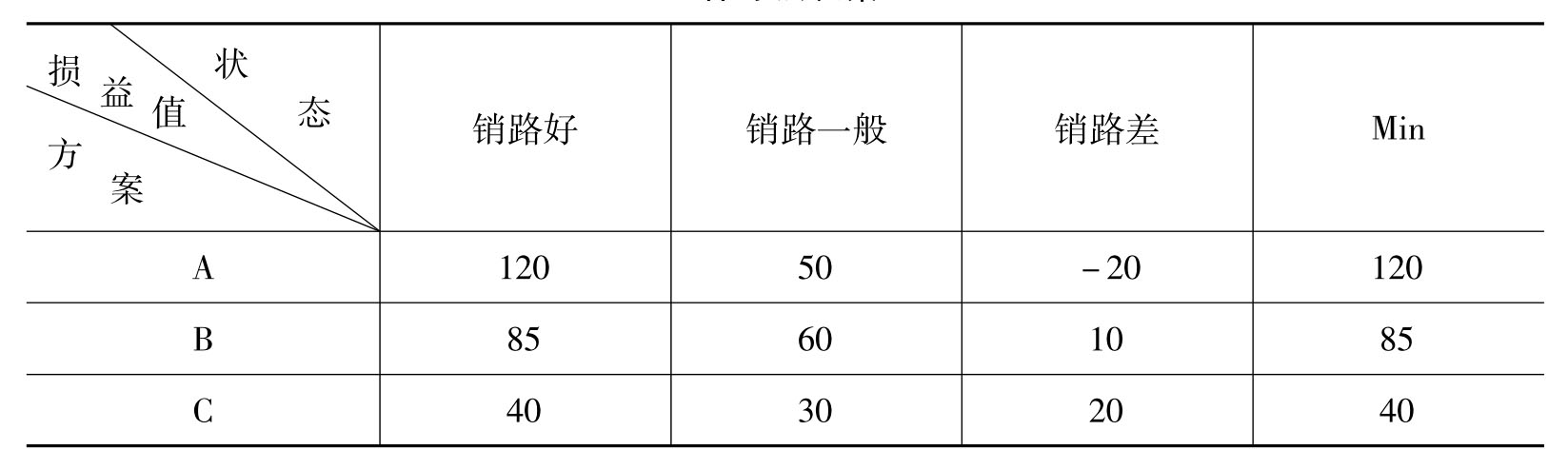
与冒险法相反，保守法的决策者在进行方案取舍时以每个方案在各种状态下的最小值为标准(即假定每个方案最不利的状态发生)，再从各方案的最小值中取最大者对应的方案。以表4－2为例，保守法决策结果见表4－3。

用保守法决策时先找出各方案在各种状态下的最小值，即{－20，10，20}，然后再从中选取最大值:max{－20，10，20}=20，对应的方案C即为用保守法选取的决策方案。该方案能保证在最坏情况下获得不低于20单位的收益，而其他方案则无此保证。

表4－3　保守法决策

(3)折中法

保守法和冒险法都是以各方案不同状态下的最大或最小极端值为标准。但多数场合下决策者既非完全的保守者，亦非极端冒险者，而是介于两个极端的某一位置寻找决策方案，即折中法。

折中法的决策步骤如下:

第一，找出各方案在所有状态中的最小值和最大值。

第二，决策者根据自己的风险偏好程度给定最大值一个系数。(0＜a＜1)，最小值的系数随之被确定为1－a。a也叫乐观系数，是决策者冒险(或保守)程度的度量。

第三，用给定的乐观系数a和对应的各方案最大最小损益值计算各方案的折中收益值。

第四，取折中收益值最大的损益值对应的方案为所选方案。

仍以表4－2为例，各方案的最小值和最大值如表4－4所示:

表4－4　折中法决策

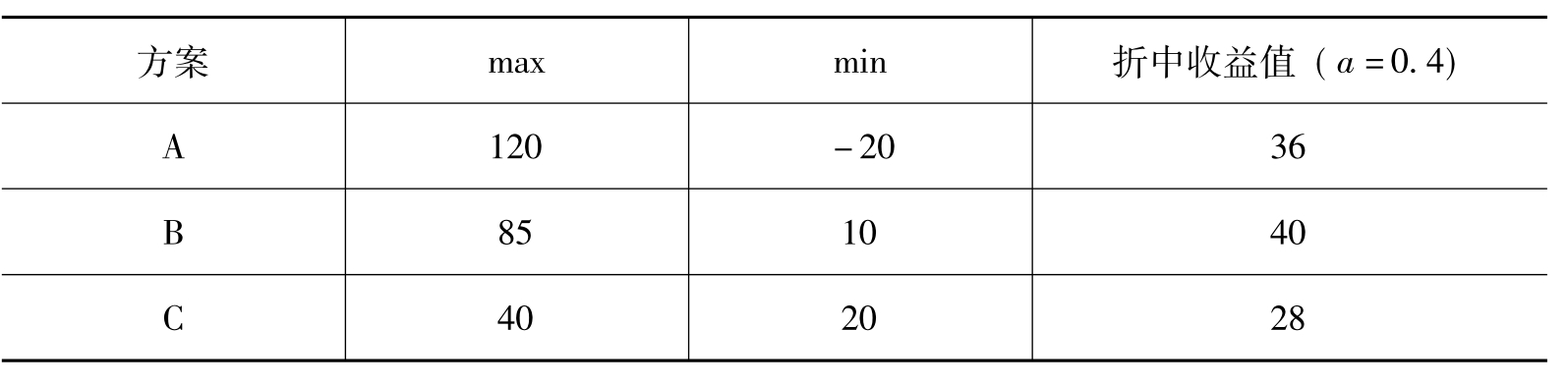
取折中收益值最大者:max{36，40，28}=40，对应的方案B即为最大值系数a=0.4时的折中法最佳方案。

用折中法选择方案的结果取决于反映决策者风险偏好程度的乐观系数的确定。当a=0时，结果与保守法相同;当a=1时，结果与冒险法相同。这样保守法与冒险法便成为折中法的两个特例。

(4)后悔值法

后悔值法是用后悔值标准选择方案的方法。所谓后悔值是指在某种状态下因选择某方案而未选取该状态下的最佳方案而少得的收益值。

后悔值法进行方案选择的步骤如下:

第一，计算损益值的后悔值矩阵。方法是用各状态下的最大损益值分别减去该状态下所有方案的损益值，从而得到对应的后悔值。

第二，从各方案中选取最大后悔值。

第三，在已选出的最大后悔值中选取最小者，对应的方案即为用最小后悔值法选取的方案。

其后悔值矩阵见表4－5所示。

表4－5　后悔值法决策

从各方案的最大后悔值中选取最小值:min{40，35，80}=35，对应的方案B即为用最小最大后悔值法选取的决策方案。

(5)平均值法

当无法确定某种自然状态发生的可能性大小，且无法确定其顺序时，可以假定每一自然状态具有相等的概率，并以此计算各方案的期望值，并以此为标准进行方案选择，这种方法就是平均值法。由于假定各种状态的概率相等，平均值法实质上是简单算术平均法。以表4－2资料为例，各方案有三种状态，因此每种状态的概率为1/3，各方案的平均值为:

A:(120+50－20)÷3=50

B:(85+60+10)÷3=51.7

C:(40+30+20)÷3=30

从各方案的平均值中选取最大值:max{50，51.7，30}=51.7，对应的方案B即为用平均值法选取的决策方案。

【本章小结】

决策是指为实现一定目标，在多个备选方案中，选择一个方案的分析判断过程。决策具有以下几个特点:第一，决策要有明确的目标;第二，决策要有若干个可行的备选方案;第三，决策要进行方案的综合分析和评估;第四，决策是一个过程。根据所要解决问题的性质和内容等方面的不同，决策可以分为不同的类型。

按决策的作用范围分类:战略决策、战术决策、业务决策;按决策的时间长短分类:中长期决策、短期决策;按决策的重复程度分类:程序化决策、非程序化决策;按决策的主体分类:群体决策、个人决策;按拟定决策的层次分类:高层决策、中层决策、基层决策;按决策问题所处的条件或环境因素的可控程度分类:确定型决策、风险型决策、不确定型决策。

决策的程序:识别问题、明确决策目标、拟订方案、评估方案、选择方案、执行方案与评价决策效果;决策的原则:满意原则、集体决策与个人决策相结合的原则及定性决策与定量决策相结合的原则;决策的影响因素:环境因素、组织文化、过去的决策、决策者对风险的态度及决策的时间紧迫性。

定性决策方法:头脑风暴法、德尔菲法与哥顿法。定量决策方法:确定型决策方法、风险型决策方法与不确定型决策方法。

【关键概念】

决策;程序化决策;非程序化决策;群体决策;个人决策;确定型决策;风险型决策;不确定型决策;满意原则;头脑风暴法;盈亏平衡分析法;决策树法;后悔值法

【复习思考题】

1.什么是决策?它有哪些类型?

2.在一个组织中，决策是否具有普遍性?为什么?

3.为什么说决策是个过程?它有哪几个重要环节?

4.决策的原则有哪几个?

5.在组织决策过程中会受到哪些因素的影响?

6.确定型决策、风险型决策、不确定型决策有何区别?在实践中如何运用各种方法?

7.请举出近3年中你所做的3个决策，试分析这些决策中哪些是程序化决策?哪些是非程序化决策?

8.某食品商场经销各种食品，其中一种食品进货价是3元/个，出售价是5元/个。如果这种食品当天卖不出去，就要造成损失1元/个。根据以往的销售情况，这种食品每天的销售量可能为1000、2000和3000个。商场经理要决定每天进多少货才能获得最大利润，试给出不同类型的商场经理可能采取的决策方案。(假设乐观系数为0.6)

9.某公司为生产一种新产品需要新建一个工厂。建厂有两个方案:一是建大厂需要投资300万元，市场销路好时每年可获利100万元，销路不好时将损失20万元;二是建小厂，需要投资160万元，在市场销路好时每年可获利40万元，销路不好时也可获利10万元。两个方案生产新产品的期限都是10年。根据市场预测，在该产品生产的前3年销路好的概率为0.7，而如果前三年销路好，后七年销路也好的概率为0.9;如果前三年销路差，则后七年销路一定差。试确定10年中哪个方案获利较大。