费恩曼物理学讲义：电子实验探索电子位置的相对概率

2025-09-30 理论教育版权反馈

【摘要】：现在我们想象一个用电子做的类似实验。在这个电子的实验中，我们注意到的第一件事是听到探测器发出尖锐的“卡嗒”声。与子弹的实验一样，我们现在开始从实验上寻找下列问题的答案：“‘整颗’电子到达后障上离中心之距离为不同的z处的相对概率是多少？”像前面一样，在保持电子枪稳定工作的情况下，我们可以从观察“卡嗒”声出现的速率来得出相对概率。

现在我们想象一个用电子做的类似实验。图1—3中描绘了此实验的概略图。我们制造了一把电子枪，它包括一根用电流加热的钨丝，外面套有一个开有小孔的金属盒，如果钨丝相对金属盒处于负电位时，由钨丝发射出的电子将被加速飞往盒壁，其中有一些会穿过盒上的小孔。所有从电子枪出来的电子都带有（差不多）相同的能量。在枪的前方也有一堵墙（就是一块薄金属板），墙上有两个小孔。这道墙的后面有另一块作为“后障”的板。在后障的前面我们放置一个可移动的探测器。它可以是盖革计数器，或者更好一些，是一台与扩音器相连的电子倍增器。

我们应当直接了当地告诉你不要试着去做这样一个实验（虽然你可能已做过我们所描述的前面两个实验）。这个实验从未以这样的方式做过。问题在于，为了显示我们所感兴趣的效应，仪器的尺寸必须小到制造不出来的程度。我们做的是一个“理想实验”。之所以要选它，是因为它易于想象。我们知道这个实验会得到怎样的结果，因为有许多已经做过的实验，在那些实验中，已在选用的适当的尺度与比例上显示了我们将要描写的效应。

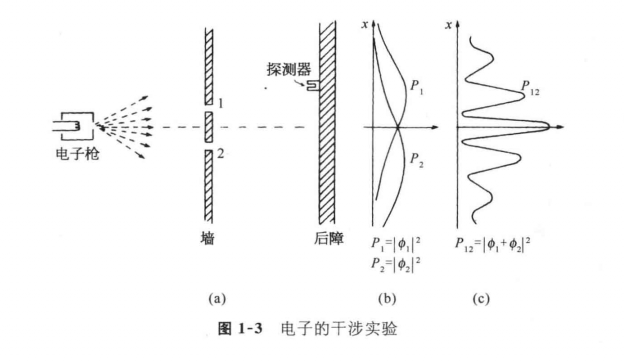
在这个电子的实验中，我们注意到的第一件事是听到探测器（即从扩音器）发出尖锐的“卡嗒”声。所有的“卡嗒”声全都相同，决没有“半卡塔”声。

我们还会注意到“卡嗒”声的出现很不规则。比如像：卡嗒……卡嗒一卡嗒……卡嗒……卡嗒……卡嗒一卡嗒……卡嗒，等等，无疑，这就像人们听到盖革计数器工作时的声音一样。假如我们计数在足够长的时间内——譬如说在许多分钟内——听到的卡嗒声的数目，然后再在另一个相等的时间间隔内再进行一次计数，我们发现两个数值非常接近。所以，我们能够谈论“卡嗒”声出现的平均速率（平均每分钟多少次卡嗒声）。(https://www.chuimin.cn)

在我们移动探测器时，声响出现的速率有快有慢，但是每次“卡嗒”声的大小（响度）总是相同的。假如我们降低枪内钨丝的温度，卡嗒声的速率就会减慢，但是每一声“卡嗒”仍然是同样响。我们还可以注意到，如果在后障前分别放置两个探测器，那么这一个或那一个将会“卡嗒”发声，但是决不会二者同时发声（除非偶尔两次“卡嗒”声在时间上非常靠近，以致我们的耳朵可能辨别不出它们是分开的响声）。因此，我们得出结论，任何到达后障的东西总是呈“颗粒”的形式。所有的“颗粒”都是同样大小：只有“整颗”到达，并且每一次只有一颗到达后障。我们说：“电子总是以完全相同的‘颗粒’到达。”

与子弹的实验一样，我们现在开始从实验上寻找下列问题的答案：“‘整颗’电子到达后障上离中心之距离为不同的z处的相对概率是多少？”像前面一样，在保持电子枪稳定工作的情况下，我们可以从观察“卡嗒”声出现的速率来得出相对概率。颗粒到达某个特定z位置的概率正比于该处的卡嗒声的平均速率。

费恩曼物理学讲义：电子实验探索电子位置的相对概率

相关推荐