医疗技术进步影响医疗费用增长的研究

2023-11-28 理论教育版权反馈

【摘要】：6.6.2基于期望寿命的医疗费用支出函数设e（x，t）表示t时刻、所患疾病x的个体能够被成功治愈的期望寿命。

6.6　医疗技术进步对医疗费用增长影响的一个理论模型

按照Jones（2002）的研究思路，来建立医疗技术进步与医疗费用之间关系的一个理论模型，旨在解释医疗技术进步与我国医疗费用增长之间的关系。

6.6.1　基于疾病的医疗费用支出函数

Jones认为，医疗技术进步主要从两个方面影响医疗费用支出：一是技术进步使以前一些无法治愈的疾病和其他健康问题现在能够以某种代价得以治疗；二是随着时间的推移，技术改良与技术革新将不断降低已有治疗方法的成本。典型例子就是我国结核病的治疗。最初，我国治疗结核病的成本是非常之高，但是，现在治愈这种疾病的成本很低。如果用x∈[0，∞）表示疾病范围。x值越大，表明疾病的治愈难度越大。众所周知，由于受医疗技术发展水平的限制，并不是所有的疾病都能治愈，并且随着时间的推移，能够治愈的疾病也不同，假设在某一时点t，能够被治愈的疾病记为[0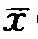，（t）]。

一般来讲，医疗费用支出h不仅与疾病x有关，而且也与时间t有关。Jones将个体所患的疾病x和时间t看做其医疗费用支出h的内生变量。为了研究上的方便，Jones假设它们之间的关系是一种指数关系。对于某种疾病x，最初治疗该疾病的技术被发明时，成本（临床应用的成本）一般会比较高。作为例证，美国和英国的医疗技术差不多，但美国的人均医疗费用比英国高出很多，原因就在于美国存在大量的临床技术。另外，就某种疾病的严重程度来讲，当针对这种疾病的治疗技术首次发明后，治疗该疾病的成本依赖于该疾病的严重程度，并且会随着该疾病的严重程度的提高而增加，设增加的指数化比率为β。那么，xβ就表示针对疾病x，治疗该疾病的技术发明后而使医疗费用增加的部分。然而，当初始的治疗技术被发明后，随后的技术进步会使这种疾病的治疗成本减少，设减少的指数化比率为γ。因此，在某一时点t，治疗某种疾病x的成本h（x，t）可以表示为：

式中，h0表示t＝0时治愈疾病x的费用；δ（x）表示首次发明对疾病x能够成功进行医治的成本的指数化比率。假设δ（x）可以表示为：

式中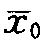，表示在时间t＝0时的医疗知识边界；α表示医疗技术进步使这种知识边界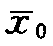变动一个单位所需要的年份。

在模型（6-1）中，技术进步会从两个不同方面影响到医疗支出。一方面，技术进步使过去不能医治的疾病得以医治；另一方面，治愈的成本非常高。

模型（6-1）是基于疾病的医疗费用（成本）函数。需要指出的是，该模型只具有理论上的意义。对此，Jones对模型（6-1）进行了改进，将期望寿命作为医疗费用支出的内生变量，在Jones看来，期望寿命的提高是医疗技术进步的结果。

6.6.2　基于期望寿命的医疗费用支出函数

设e（x，t）表示t时刻、所患疾病x的个体能够被成功治愈的期望寿命。^[14]期望寿命依赖于未来的技术进步。e的单位变化是指假设所有〕可能利用的技术都已使用的情况下预期生存的年份，e测量的是生命的期望长度。需要指出的是，像有些技术可能太贵，患者承担不起费用，结果患者不会使用，对于这种情况，患者可能只会等待死亡。与此同时，假设对于任何一个人，如果他（她）感染了某种疾病而不进行治疗都会死亡。^[15]而对某些技术，尽管使用的成本可能比较高，但使用后可能会延〕长患者的寿命。假设e（x，t）通过下式给出：

上式表示，个体所患的疾病越不严重，其期望寿命越高。另外，对感染了可以医治的最为严重的疾病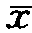（t）的个体来讲，其期望寿命则下降到0。

若用h（e，t）表示t时刻、期望寿命为e的个体的医疗费用支出函数。则由模型（6-1）比较容易得到h（e，t）的表达式如下：

这里，

且

模型（6-4）作为技术进步与医疗支出之间关系的基本模型。模型（6-）解释如下：在期望寿命水平一定的条件下，随着时间的推移，医疗支出将提高，提高的比率为μ≡β/α。表达式中β反映了这样一种事实，在一定的期望寿命水平下，随着时间的推移，人们遭受了更为严重、并且治疗的成本更高的疾病。比如，目前经济条件下，患有最为严重疾病的人的医疗成本比20世纪50年代患有最为严重疾病的人的医疗成本高出很多。因为技术进步使得能够治疗的边界医疗条件发生了显著性的变化，使得原来许多不能医治的疾病得以医治。

模型（6-4）也描述了在某一时点上人的医疗支出的分布。临近死亡的人医疗支出最高（与本书第4章的主张一致），并且随着期望寿命的提高，医疗费用支出将按指数比率θ下降。期望寿命越低的人，医疗费用支出越高。正如在方程（6-6）所看到的，这里有两方面的原因：首先，如果某人得了比较严重的疾病，会使治疗的成本提高比率μ（指数化）；其次，对这种比较严重的疾病的最初治疗方法最近才发现。意味着为了减少治疗成本，与γ相联系的能够减少治疗成本的技术进步治疗的时间比较少。

从方程（6-2）中容易得到t＝δ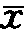（（t））因此，人口中最高的期望寿命由下式给出：

e（0，t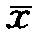）＝（t）＝x0＋t/α

若用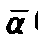（t）表示人口中最高的期望寿命，则有：

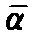（t）≡e（0，t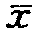）＝0＋t/α　　　　　　　（6-7）

由于技术进步，期望寿命每隔α年提高1年。White（2002）研究显示，这种线性公式非常适合于20世纪的后半个世纪的高收入国家的数据，并且α大约等于5。

6.6.3　模型中的人口分布、时间选择(www.chuimin.cn)

人口分布。为便于分析，假设人的期望寿命服从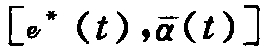上的均匀分布。其中，e*（t）表示增加治疗可以换取的寿命。如果所有可能利用的技术都被利用了，e*（t）将等于0；反之，如果某些技术还没有使用，e*（t）将大于0。例如，e*＝2的含义在于，如果所有治疗方法已经使用，这个人可能生存2年后就会死亡。表示人口中最高期望寿命，则有：

a*（t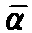）≡（t）－e*（t）　　　　　　　（6-8）

对于e来讲，人口是服从均匀分布的，它表示t时的人口规模。既然假设e是服从均匀分布的，那么，期望寿命的提高意味着人口规模的增长。

时间选择。时间可以采用连续与离散两种情况，这里则选择离散型情况。在一个时期的开始点，人们就开始承担了他们的医疗支出，并且在那个时期生存下来。在时期t，期望寿命的取值范围为[e^*（t），e^*（t）＋1），并且人在那个时期结束时会死亡。

6.6.4　医疗总费用H（t）

这里，医疗总费用H（t）由下式给出：

利用方程（6-4），可以直接得到：

最后，只要θa（t）的值足够的大（通常能够满足），从式（6-11）可以得到近似等式：

使用等式（6-4），可以用指数代替（6-12），得到：

6.6.5　考虑医疗保险情况下的医疗支出函数

前面的讨论都没有考虑医疗保险的作用。实际上，医疗保险的存在会通过相对价格的下降使患者的医疗支出增加。下面，将考虑医疗保险的存在情况下技术进步对医疗支出的影响效果。

在某一时点，某些人接近生命的结束，因而面临比较大的医疗支出。那么这些人如何解决他们所面临的这种风险呢？假设这些面临死亡的人在其生命结束前的医疗费用支出为人均收入的σ倍。一方面，有些人也许购买了医疗保险，他们只需要承担部分医疗费用，这样，他们可以留下更多资源用于消费和储蓄。因此，σ值可能较小；另一方面，众所周知，一些人为了规避这种风险，会从年轻时代开始就可能采取储蓄措施，这样会使σ取比较大的值。显然，σ值可能大于1也可能小于1，并且σ值不会随着政策的变化而变化。这里只考虑个体购买了医疗保险的情况，因此，σ采用递减形式，且σ对所有人都是相同的。

个体购买了医疗保险后，保费支付后的利益依赖于个体的健康状况。医疗技术的迅速发展，使得人在生命的最后一年生存的成本比人均收入增长得更快（＞g）。在某一时刻，即使现存的技术可以延长一μ个人的生命，但由于个体需要支付的医疗费用可能超过了他的承受能力，患者也不会使用这种技术。把这种情况发生的时刻记为t* 。 t*由以下方程求得：

h（0，t^*）＝σy（t）　　　　　　　　　（6-13）

在日期t^*之前，人们能够支付他们自己的医疗费用。当t＝t^*时，医疗费用由等式（6-12）给出，且e^*（t）＝0。也就是说，只要技术上是可能的，人就能生存。

在时刻t^*之后，情况发生了变化。尽管技术上存在可能延缓人的寿命的技术，但由于技术使用的成本可能超过他们的承受能力（预算约束）。在不存在保险覆盖的情况下，某些人可能会面临死亡。

个体购买了医疗保险之后，在保险的保障范围内，个体可以通过保险公司的保险金给付υ（e，t），使患者生命得以延续直到保险金给付完为止。即：

这里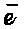（t）表示一个人的边际期望寿命所要求的保险金给付。（t）由下式确定：