垄断竞争下供给引致需求及质量提供：研究结果

2023-11-28 理论教育版权反馈

【摘要】：在某一时间间隔内，市场上有S个提供者，他们在引致与质量之间展开竞争，M个人中有N个人接受了医疗服务。在任何情况下，医生不单单追求引致行为或者追求医疗服务质量的提高，而是选择一个数量和质量组合以最大化其效用。

5.5　垄断竞争条件下供给引致需求与质量提供

5.5.1　假设条件

（1）医疗服务市场是一个垄断竞争市场。在某一时间间隔内，市场上有S个提供者，他们在引致与质量之间展开竞争，M个人中有N个人接受了医疗服务。

（2）为了研究上的方便，假设医疗服务的价格不变。^[14]医疗服务过程中不存在引致的伦理道德成本或者引致的财务成本。

（3）患者是同质的，患者对医疗服务的质量不能做出评价。因此，就患者所接受的医疗服务量来讲，诊疗的效用是不变的。一旦患者选择某个医生j，患者会被动地接受医生的建议。

在任何情况下，医生不单单追求引致行为或者追求医疗服务质量的提高，而是选择一个数量和质量组合以最大化其效用。

下面按照Farley（1996），De Jaegher和Jegers（2000）以及Daniele Fabbri（2001）的分析思路，医疗服务需求分两阶段进行考虑。第一阶段，首先由患者依据其效用最大化的原则选择医生；第二阶段，由医疗服务的提供者间接决定患者的医疗服务量。

5.5.2　模型

从需求层面来看，在不存在引致的情况下患者应该必须消费一定的医疗支出，其值用c表示。为使模型简单化，这里假设c＝1，即患者必须至少消费一个单位的医疗服务。患者的医疗支出会随着所选择的医生的引致效果的增加而增加；医疗服务的质量并不会引起引致需求，因而也不会增加个体的医疗支出。但是，引致的边际生产力随着医疗服务质量的提高而提高。

基于上述考虑，患者选择第i个医生的医疗支出可以用下式表示：

y_i（x_i）＝1＋α（1＋q_i）x_i　　　　　　　　　（5-8）

式中，y_i（x_i）表示患者选择第i个医生的医疗支出，它随着医生对患者的引致需求xi的变化而变化；q_i表示医疗服务的质量；α表示影响因素。

患者一旦接受了医生的治疗，他们会观察到q_i和x_i的价值，并且患者就医生的q_i和x_i情况会在他（她）们的亲戚、朋友之间进行传递。患者之间的这种“口传广告”实际上就是像医疗这种“名声”产品市场的一个典型特征。在这些市场上，消费者搜寻提供者主要是通过亲戚、朋友以及邻居的推荐进行的。

患者在不同的提供者中做出选择，是根据两个相关的特征进行的，即提供者所产生的医疗服务的质量水平以及引致效果，因此，患者的效用可以看做是医生的医疗服务质量与引致效果的函数。进一步地，可以设患者的效用函数如下：

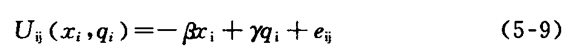
而患者选择提供者，是为了最大化上述随机效用函数。上式中，－β和γ分别表示引致的边际负效用和医疗服务质量的边际效用，e是随机误差项，表示影响患者选择的一些尚未观察到的因素。在这里，引致效果以负的形式进入到效用函数。

为了得出选择第i个医生的概率，必须对e′e做出假设。这里假设当且仅当ee独立同分布，并且服从Weibull分布。选择第i个医生的概率才具有下列的逻辑（Logistic）分布函数形式：

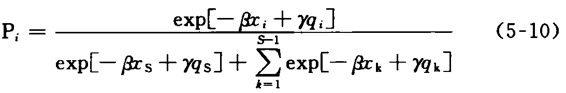
这里的qs和xs分别是相关提供者的质量和引致水平。因此，即使医疗服务的质量提高了，由于引致效果使得第i个医生所拥有的患者份额减少。这里，顺便指出的是，只要某个地区的医生数目增加，那么消费者关于每一个医生的信息就会减少。如果医生的数目很小，例如为3个，而对消费者来讲，他们的朋友中有可能都到这三个医生那里去看过病，并且消费者也记得他们的朋友对这三个医生的评价，那么每一个医生在这个社区内都有一个详细的名声。然而，如果这个社区内医生比较多，例如30个，那么对每一个医生的名声就不好定义了。因此，医生数目的增加使得搜寻特定医生的困难增加，因而使得消费者对选择属性就不那么敏感。

若令B_i＝N×P_i，于是，可以将某个医生i所提供的医疗服务需求定义为：

Q_i＝B_i×y_i（x_i）

现在考察提供者——医生的利润函数。S个提供者在质量与引致之间进行竞争。如果引致是没有成本的，那么，医生为了增加患者的需求可能会采取引致手段。换句话说，生产质量是有成本的，假设其成本占总固定成本的比例为δ，整个成本函数由下式给出：

C_i（x_i，q_i）＝cx_i＋δq_i　　　　　　　　　（5-11）

因此，质量提高增加了患者的医疗支出，与此同时增加了第i个医生的所拥有的患者的市场份额。如果它对固定成本的影响的比例为δ，引致增加了患者的医疗支出，但是它会减少拥有患者的市场份额。

如果对各种成本的补偿保费为Δ＝p－c。于是，可以定义医生的利润函数如下：

R_i（x_i，q_i）＝B_i[1＋α（1＋q_i）x_i]Δ－δq_i　　　　　　　　　（5-12）

5.5.3　均衡分析

现分析均衡时的q和x的水平。首先假定q一定，为了确定第二阶段的x，令R_i（x_i，q_i）对x_i的偏导数等于0，得到：

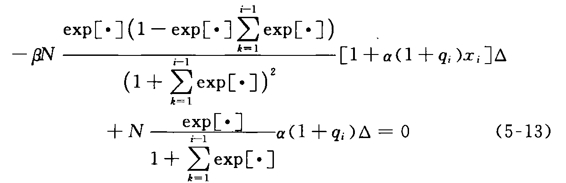
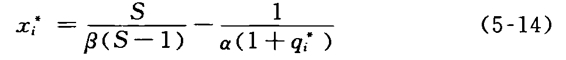
若对任意给定的i，令x_i=x_s,q_i=q_s,得到：上式表示，在均衡水平下，引致水平随着质量水平的提高而提高。将x*代入利润函数中，令Ri（xi，qi）对qi的偏导数等于0，得到：

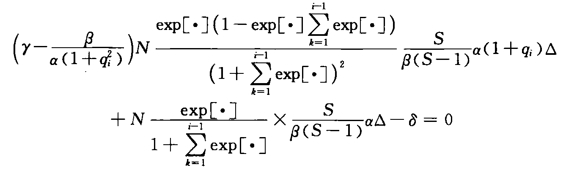(www.chuimin.cn)

在上式中，同样地令x_j=x_s,q_i=q_s,解方程得到：

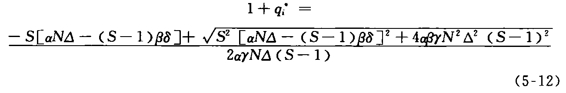
5.5.4　讨论

由于患者的效用不能取负值，即对于x和q，必须满足－βxi ＋γqi≥0。因此，x和q的取值受到限制。易知x和q取值必须满足：q*＞0且x*≥0。

由式（5-15）比较容易推得：

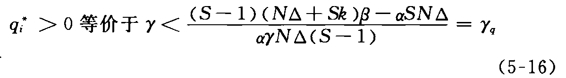
用q*的值代入式（5-14），则有：

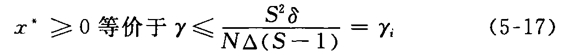
即：

一般地，在医疗服务市场上存在这样一种现象：患者数目（不是治疗）的增加会刺激医疗服务质量的提高。这种现象通常称之为医疗服务的“纯实际效果”。倘若质量的边际成本等于（或大于）边际收益，则均衡时不存在引致情况（严格为正）。

当引致为零即x^*＝0（称之为情况1）时，此时q^*＞0，且γ_q＞γ_i。因而有：

α ＜β（S－1）/S　　　　　　　　　　　（5-19）

换句话说，引致的边际生产力必须比引致的边际负效用小。因此，就医疗服务质量来讲，只要式（5-18）或（5-19）正确，情况1就会出现。为了保证患者的效用非负（称之为情况2），式（5-18）必须正确。并且，只要式（5-18）的严格不等式成立，情况2就会出现。在引致的边际生产力小于引致的边际负效用情况下，由于“纯实际效果”，假如质量的边际成本等于或大于边际收益，我们就可以得出有意义的解。各因素变化对医生医疗服务的质量提供以及引致水平的影响效果见表5-4。

表5-4　各因素变化对质量提供与引致水平的影响效果

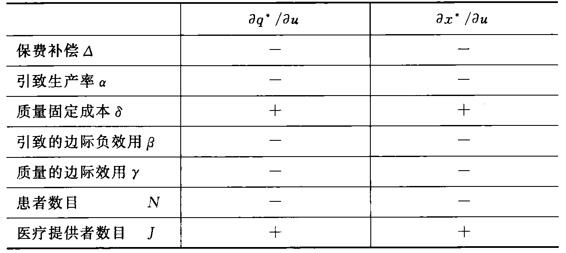
从表5-4可以看出：

保费补偿越大（越小），则引致需求以及提高医疗服务质量的动机越低（越高）；反之，引致的边际生产力越低，则引致和质量越高。

只要质量提供的边际成本增加，生产者往往会抵消因引致与质量提高所带来的收入变动。对质量提供的边际成本的实施补偿，一方面会减少医生过分提供的动机，另一方面会降低医疗服务的质量。

质量上的边际效用增加同时会减少引致和质量。相反，引致的边际负效用的增加，会引起医疗服务质量以及引致的减少。这意味着，改善患者对医生引致行为的了解会使患者的福利得到改进。

5.5.5　模拟

为了得到在垄断竞争条件下，医生数目S的增加以及引致的边际负效用β增加对医疗服务质量的影响效果，现对上述模型进行简单的模拟。即分别假定其他的变量取给定值的情况下，S增加或者β增加对医疗服务的影响效果。一般来讲，患者在选择医生时，相比引致，患者对质量更敏感。因此，在对模型模拟的过程中我们假定γ＞β。另外，由于式（5-18）必须正确，因此，变量取值还应满足β＜S²δ/NΔ（ S－1）。

首先分析S增加对医疗服务的影响效果。这里假设β＝0.05，γ＝0.20，Δ＝0.20，N＝1，000，δ＝8，α＝0.03，S分别取3，4，5，6，7，8，模拟结果如表5-5

表5-5　S增加对医疗服务的影响

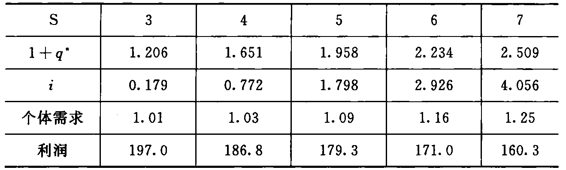
根据表5-5，医生数目的增加会对质量产生正的效果，但是同时会带来诊疗的过分提供，尽管患者的医疗需求会增加，但医生的利润往往会减少。

接着再来分析β增加对医疗服务的影响效果。这里γ、N、δ、α取值同上，J＝3，而β分别取0.05，0.06，0.07，0.08，0.09，0.10，模拟结果见表5-6。

表5-6　β增加对医疗服务的影响效果

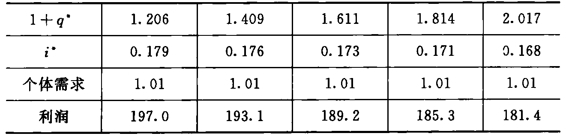
从表5-6可以看出，引致的边际负效用的增加，一方面使得医生的质量提供提高，另一方面，医生的引致水平下降；尽管患者的医疗需求不变，但医生的利润会下降。

垄断竞争下供给引致需求及质量提供：研究结果

相关推荐