由于CO2对人体没有严重危害,加之《京都协议书》的CO2减排任务主要针对发达国家,中国目前还无需承担减排CO2责任。研究提出作为水电为主体的“西电东送”开创了中国式的CDM机制的观点。CDM机制及项目通常产生在不同国家之间。......
2023-11-28
5.6 指标量化与权重系数的确定
权重系数表示某项指标在指标系统中的重要程度,其大小和目标与其所占评价中时的重要程度相关。本研究采用层次分析法(Salty,1996;陈伟,2000)来确定指标权重。
5.6.1 层次分析法AHP
1.层次分析法AHP简介
AHP即Analytic Hierarchy Process,又称层次分析法,是由美国著名运筹学家、匹兹堡大学教授Saaty于20世纪80年代创立的(陈伟,2000)。这是一种定性和定量相结合的、系统化的、层次化的分析方法,是一种用于可处理复杂的社会、政治、经济、技术等方面决策问题的分析方法。
2.基本原理
AHP的原理是(Barizilai,1994),根据人的思维规律,面对复杂的选择问题,将问题分解成各个组成因素,再将这些因素按支配关系分组形成递阶层次结构,通过两两比较的方式确定层次中诸因素的相对重要性。这—思维过程的关键是层次的划分、权重的确定和排序的并合规则。
3.层次分析法AHP的基本步骤
基本步骤包括(Dyer,1990)建立树状递阶层次结构模型,一般表现为评估指标体系之后需要确立思维判断定量化的标度。
(1)递阶层次结构的建立
AHP法首先把问题层次化,按问题性质和总目标将此问题分解成不同层次,构成一个多层次的分析结构模型,分为最低层(供决策的方案、措施等),相对于最高层(总目标)的相对重要性权值的确定或相对优劣次序的排序问题。将决策问题分解为几个层次,最上层为目标层A,最下为具体指标层C,中间层为准则层B。
(2)建立两两比较的判断矩阵
判断矩阵表示针对上一层次某单元(元素),本层次与它有关单元之间相对重要性的比较。通过相互比较来确定各个准则对于目标的权重及各方案对于每一准则的权重。
(3)将方案层对准则层的权重及准则对目标层的权重进行综合,最终确定方案层对目标层的权重。在层次分析法中要给出进行综合的计算方法,最后给出决策结果。
在同一层次两个因素互相比较时,考虑到专家对若干指标直接评价权重的困难,根据心理学家提出的“人区分信息等级的极限能力为7±2”的研究结论(Salty,1996;陈伟,2000),AHP方法在对指标的相对重要程度进行测量时,引入了九分位的相对重要的比例标度,构成一个判断矩阵A。矩阵A中各元素Bij表示横行指标Bi对各列指标Bj的相对重要程度的两两比较值(B为A的下一级指标)。
表5-1 层次分析法AHP九分位比例标度
Tab.5-1 Analytical Hierarchical Process AHP nine-bit ratio scale

4.层次分析法AHP的具体步骤
具体步骤包括(Dyer,1990):
第一,构造判断矩阵。运用两两比较方法,对各相关元素进行两两比较评分,根据中间层的若干指标,可得到若干两两比较判断矩阵。判断矩阵A是一个正交矩阵,每次判断时,只需要作n(n-1)/2次比较即可。
第二,计算各判断矩阵的特征向量。
第三,计算结果经归一化处理后即为下级各要素对上级某要素的权重。
5.6.2 运用层次分析法确定指标的权重
能源地理空间配置的综合效应由能源效应、环境效应、经济效应、社会效应共同组成,其中能源与环境效应在以前的效应评价中往往是被忽视的,在本研究中恰恰是作为重点要被突出强调的。判断矩阵中的bij是根据资料数据、专家的意见和系统分析人员的经验经过反复研究后确定。有鉴于此,经征求专家意见后(采用主观判断法),构造出准则层B相对于目标层A的判断矩阵:
指标量化一般采用专家经验判断(Dyer,1990)。专家凭借自己的经验,综合当时的政治经济发展形势,以及以往年份同类项目、单位或部门使用同类资金所产生的经济效益和社会效益,并结合一定的经验,对该项指标的重要程度做出经验判断。本研究采取问卷调查,请专家对指标体系中的指标进行两两比较。采用规范平均法来计算矩阵的权向量W和一致性指标CI。
表5-2 层次分析法目标层A的判断表及计算表
Tab.5-2 AHP judgments of target layer A and the computation the table
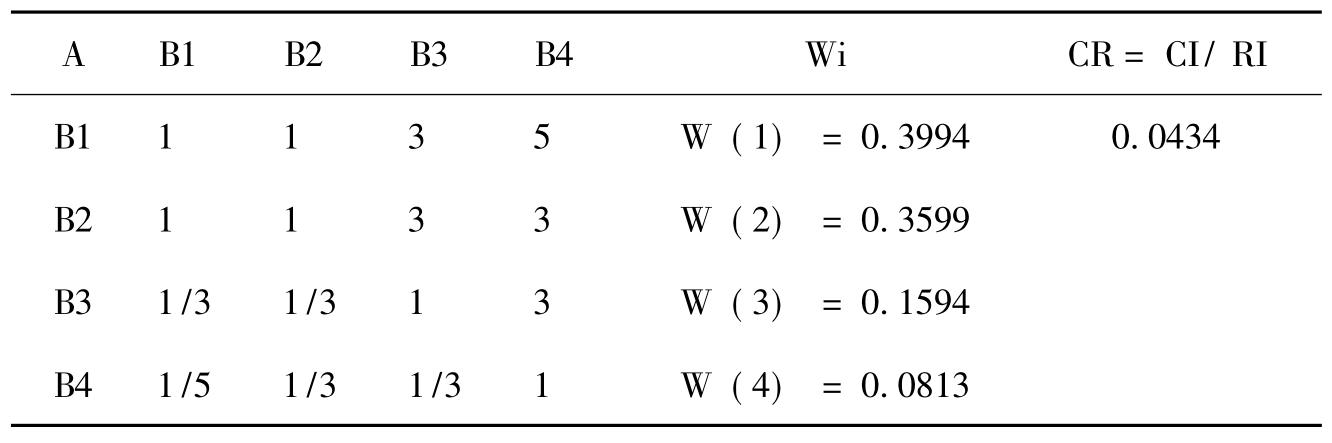
表5-3 层次分析法目标层A矩阵一致性检验结果
Tab.5-3 AHP consistency target layer A matrix of test results
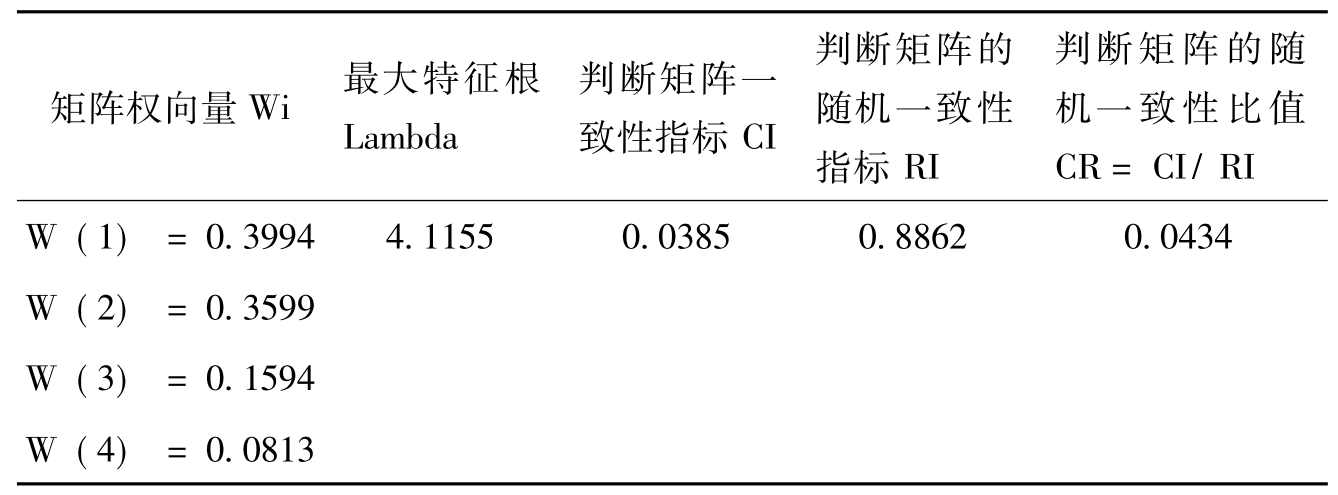
表5-4 层次分析法指标层B1的判断及计算表
Tab.5-4 AHP judgments of index layer B1 and the computation table
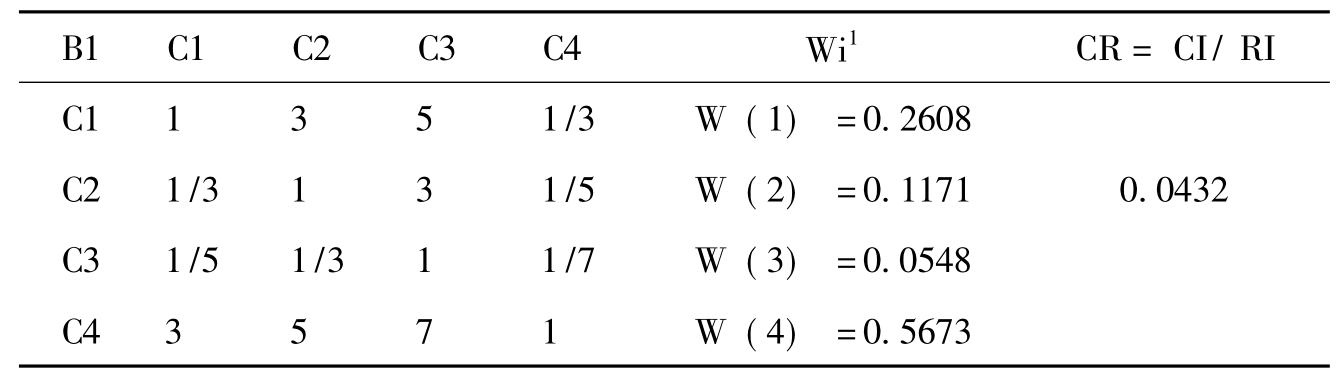
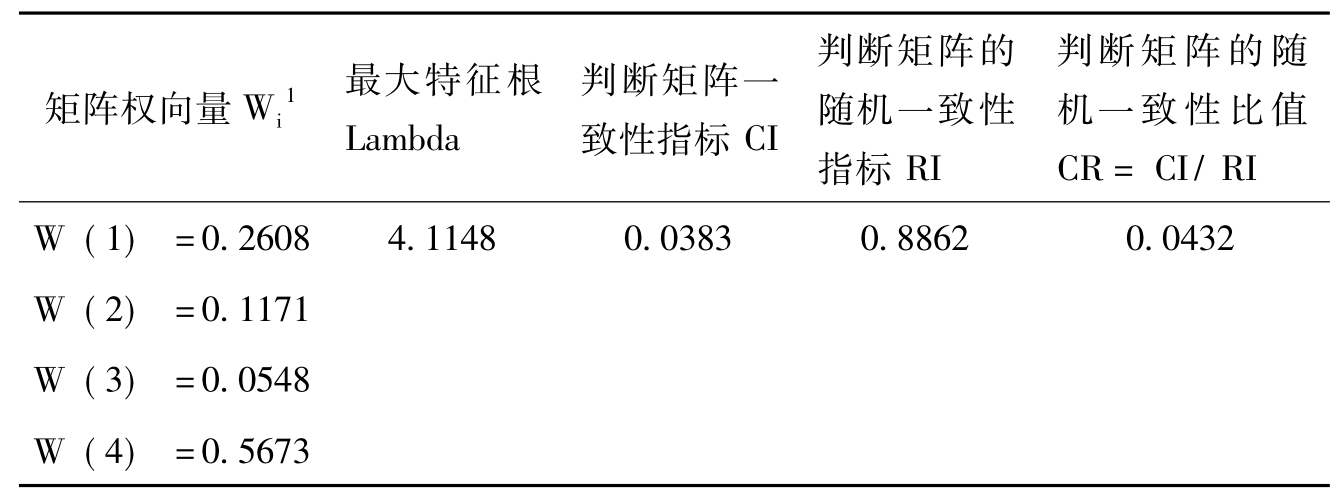
表5-5 层次分析法指标层B1矩阵一致性检验结果
Tab. 5-5 AHP consistency index layer B1 matrix of test results
 (www.chuimin.cn)
(www.chuimin.cn)
表5-6 层次分析法指标层B2的判断及计算表
Tab.5-6 AHP judgments of index layer B2 and the computation table
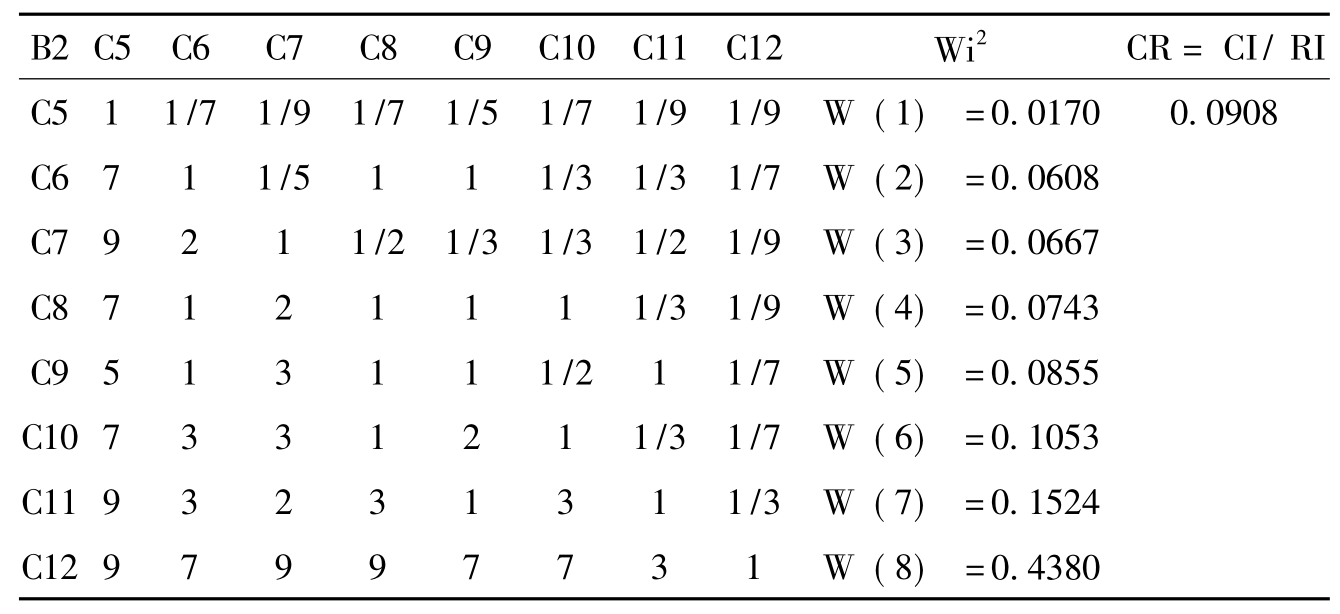
表5-7 层次分析法指标层B2矩阵一致性检验结果
Tab.5-7 AHP consistency index layer B2 matrix of test results

环境效应指标B2包含输出区的生态损失。尽管目前还未有准确的统计灾害数据,但在指标体系的权重不能忽略。关于污染物的减排量的重要性排序,主要通过专家打分,依据是各种污染物按对人体的危害性、经济价值、治理成本来定夺他们的重要性。
表5-8 层次分析法指标层B3的判断及计算表
Tab.5-8 AHP judgments of index layer B3 and the computation table
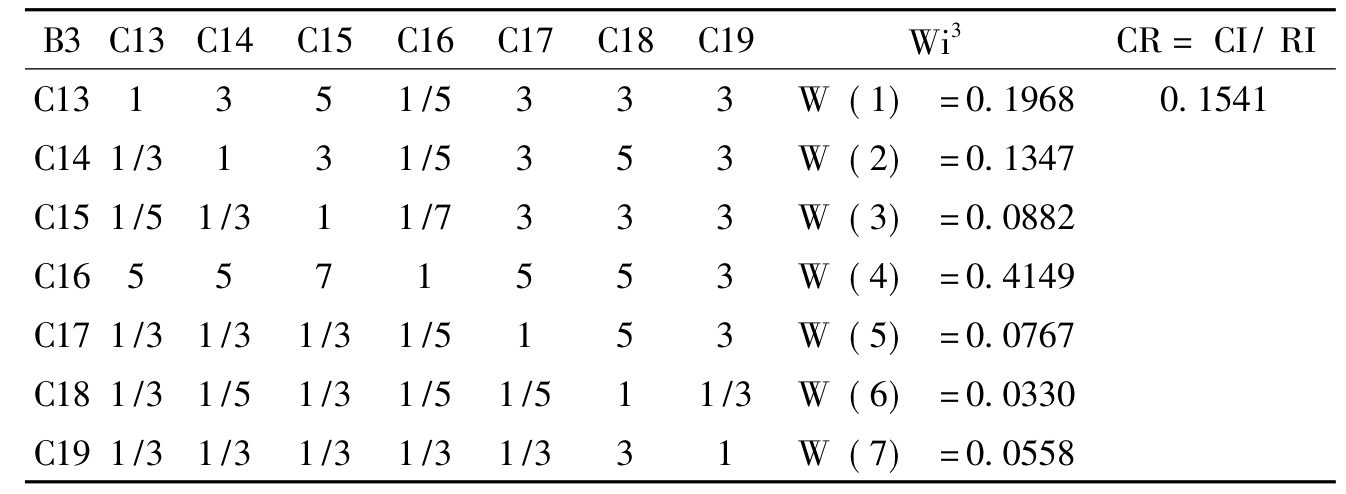
表5-9 层次分析法指标层B3矩阵一致性检验结果
Tab.5-9 AHP consistency index layer B3 matrix of test results

在经济效应指标B3中,共有7个子指标。其中C16这一个指标,本研究是用直接前向联系、全部前向联系(电力对其他行业的支撑拉动作用)、直接后向联系、全部直接后向联系(其他行业对电力的支撑作用,即电力行业每增加一价值单位,需要其他行业投入的价值)这四个子指标来反映产业互动效应的,由于西电的产业拉动效应主要体现在输出区的电力行业,因此本研究专门分析计算了电力行业与其他行业之间的互动关系。用2002年投入产出分析表可以计算出电力行业与其他行业之间的相关系数,并且用这四个小指标的系数加权平均,来反映产业拉动效应,衡量产业拉动对上一级指标的重要性,以此结果可以作为专家打分时的依据。
表5-10 层次分析法指标层B4的判断及计算表
Tab.5-10 AHP judgments of index layer B4 and the computation table

表5-11 层次分析法指标层B4矩阵一致性检验结果
Tab.5-11 AHP consistency index layer B4 matrix of test results

上述结果表明A、B1、B2矩阵CR均小于0.1通过一致性检验,但B3、B4矩阵的CR大于0.1未通过一致性检验,需要对矩阵数值进行调整。调整后的新矩阵均通过一到性检验。
表5-12 调整后的新矩阵B3及计算表
Tab.5-12 Adjusted new matrix B3 and the computation table

表5-13 调整后的新矩阵B4及计算表
Tab.5-13 Adjusted new matrix B4 and the computation table

表5-14 层次分析法指标层B4矩阵一致性检验结果
Tab.5-14 AHP consistency index layer B4 matrix of test results

根据树状递阶层次结构模型,运用层次分析法的能源空间配置综合效应评价指标权重体系计算结果表5-15。
表5-15 运用AHP计算能源空间配置综合效应指标体系权重结果
Tab.5-15 the result of index weights calculated by using AHP of combined effect of energy space allocation
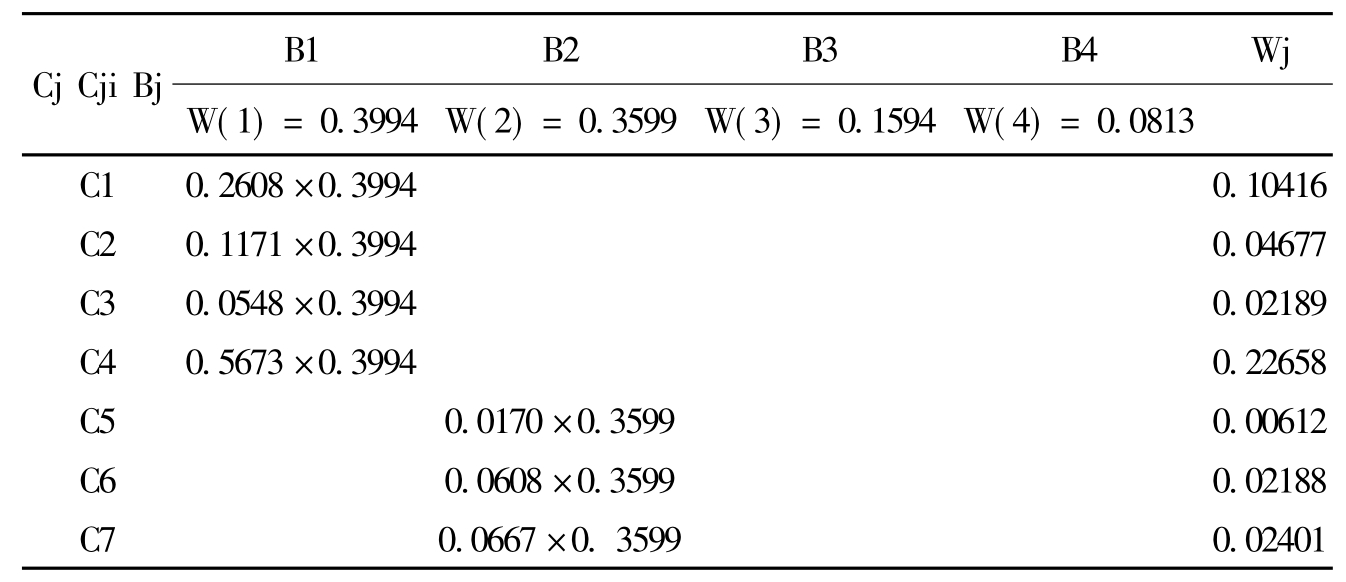
续上表

有关地理视角下能源空间配置及其综合效应研究的文章

由于CO2对人体没有严重危害,加之《京都协议书》的CO2减排任务主要针对发达国家,中国目前还无需承担减排CO2责任。研究提出作为水电为主体的“西电东送”开创了中国式的CDM机制的观点。CDM机制及项目通常产生在不同国家之间。......
2023-11-28

人们将“地表水的集水面积称为流域”,它是指一个水系的干流和支流所流经的整个区域。流域中的“区域”更多采取地理学的定义,其划分的特征便是水。②将三峡和金沙江干支流水电送往华东地区,形成“西电东送”中通道。......
2023-11-28

可持续发展评价模型与指标体系研究为本研究提供了理论依据与评价方法。概念模型试图将资源、人口、环境、经济、社会等一切因素通过量纲化处理统一以货币、能值来表达发展的可持续性,但因数据难以全面统计、价值转换中存在主观性替代了客观性等问题,致使评价模型的科学性与操作性难以兼顾。......
2023-11-28

外部性理论是由庇古提出的,是新古典经济学提出的政府干预规制市场失灵的理论基础。当边际社会成本与边际私人成本不相等导致两者有差异时,出现外部性。因此庇古手段在解决外部性问题上有制度缺陷。......
2023-11-28

9.1结论本研究以珠江流域“西电东送”为例,在构建能源地理空间配置评价指标体系的基础上,从能源、环境、经济与社会等四个方面,分析能源空间配置所产生的综合效应,包括在应对全球气候变化大背景下能源空间配置的CO2减排效应,从能源空间配置的深层动力机制出发,剖析“西电东送”区域间经济利益关系格局的调整以及跨区域多方利益主体多元目标下合作的可能性与前提条件,提出提高能源配置效应的制度框架。......
2023-11-28
相关推荐