数学面貌的大变化对数学教育提出了新的要求。改革数学教育的浪潮,席卷了世界所有发达国家。数学教育已经成为一门受到广泛重视的学科。数学教育学的对象是数学教学,而不是数学本身。于是,数学教育学要靠数学提供材料。为了数学教育的需要,对数学成果进行再创造,这已不是数学教育学的任务了。这主要是数学工作者的责任,是数学的任务。......
2023-10-17
“八仙过海”只是一个玩意儿,我们只能在游戏场中碰到它,学校里的教科书上是没有的。老实说,平常研究这些玩意儿的朋友还多是目不识丁的中下阶级的分子。然而,这些朋友专门喜欢找学生寻开心,他们会使得你惊奇,会使得你莫名其妙,最后给你一个冷嘲:“学校里念书的人这都不知道!”原来在我们中国一般人的心里都有个传统的思想,“一物不知,儒者之耻”,读书人便是儒者,所以不但应当知人之所不知,还应当知人之所知,不然就应当惭愧。传统思想自然只是传统思想,其实又有谁真能做到事事都知呢?不过话虽如此,有些小玩意儿却似乎应当知道,全都推脱,终不是一回事。“八仙过海”便是一个例子。只要肯思索的朋友,我相信花费一两个小时的时间就可以将这玩意儿的闷葫芦打破。
但是为了这一点小玩意儿,便费去一两个小时去思索,一天到晚所碰到的小玩意儿不知有多少,若都要思索,哪儿还有工夫读书、听讲?而且单是这般地思索,最好的结果也不过是一个小玩意儿的思想家,究竟登不上大雅之堂。这样一想,好像犯不上去思索了。那么为什么不将它也搬进教科书里去呢?我们读的教科书彻头彻尾是洋货,我们不自己搬进去,谁还来替我们搬不成?朋友,把我们的货色搬到他们的架子上去,这是要紧的工作。在这里,请容我再说几句闲话。我说的是把我们的货色搬到他们的架子上去,你切不可误会,以为我是劝你将他们的货色搬到我们的架子上来。我们有的是铁和铜,用它们照样造火车、造发动机,这叫将我们的货色搬到他们的架子上去;他们有的是上帝和耶稣,用它们照样和城隍财神一般地敬奉,这叫将他们的货色搬到我们的架子上来。朋友,架子是他们的好,这用不着赌气,货色却没有什么中外,都出自地壳。这虽只说到一个比方,但在我们读书的时候,它的根本含义却很重要。不过说来话长,别的时候再详谈吧。好在我要谈“八仙过海”,也就是搬我们的货色到他们的架子上的一个例子,你若觉得还有意思,那就有点儿头绪了。
我不知道你碰到过“八仙过海”这类的玩意儿没有,为了说起来方便,还是先将它说明一番。
一个人将八个钱分上下两排排在桌上,叫你看准一个,记在心头。他将钱收起,重新排过,仍是上下两排,又叫你看定你前次认准的那一个在哪一排,将它记住。他再将钱收起,又重新排成两排,这回他叫你看,并且叫你告诉他你所看准的那一个钱这三次位置的上下。比如你向他说“上下下”,他就将下一排的第二个指给你。你虽觉得有点儿奇异,想抵赖,可是你的脸色也不肯替你隐瞒了。这个玩意儿就是“八仙过海”。这人为什么会有这样的本领呢?你会疑心他是偶然猜中的,然而再来一次、两次、三次,他总不会失败,这当然不是偶然了。你就会疑心他每次都在注意你的眼睛,但是我告诉你,他哪儿有这么大的本领,只瞥了你一眼,就会看准了你所认定的那个钱?你又以为他能隔着皮肉看透你心上的影子,但是除了这一件玩意儿,别的为什么他又看不透呢?
这玩意儿的神妙究竟在哪里呢?朋友,你既然喜欢和数学亲近,大概总想受点儿科学的洗礼的,那么,我告诉你,宇宙间没有什么是神妙的。假如真有的话,我想便是“一个人有了脑筋本是会想的,偏不肯去想,但是你若要将他的脑袋割去,他又非常不愿意”这一件事实了。不是吗?既不愿用它,何必留它在脖子上?“八仙过海”不过是人想出来的玩意儿,何必像见鬼神一样对它惊奇呢?你若不相信,我就把玩法告诉你。
这玩法有两种:一种姑且说是非科学的,还有一种是科学的。前一种比较容易,但也容易被人看破,似乎未免寒碜;后一种却较“神秘”些。
第一图
先来说第一种。你将八个钱分成上下两排照第一图排好,便叫想寻它开心的人心里认定一个,告诉你它在上一排或是下一排。
第二图
第三图
譬如他回答你是“上”,那么你顺次将上一排的四个收起,再收下一排的。然后将收在手里的一堆钱(注意,是一堆,你弄乱了那就要垮台了),上一个下一个地再摆作两排,如第二图。你将两图比较起来看,一图中上一排的四个到二图中分成上下各两个了。你再问他所认定的这次在哪一排。譬如他的回答是“下”,那么第一次在上,这一次在下的只有B和D,你就先将这两个收起,再胡乱去收其余的六个,又照第二次的方法排成上下两排,如第三图。在这图里B和D已各在一排,你再问他,若他说“上”,那他所认定就是B,反过来,他若说“下”,当然是D了。
你看这三个图,我在第二图有四个圈没写字,在第三图只写了两个,这不是我忘了,也不是懒,空圈只是表示它们的位置没有什么关系。
其实这种玩法道理很简单,就是第二回留一半在原位置,第三回留下一半的一半在原位置。四个的一半是二,两个的一半是一,这还有什么猜不着呢?
我不是说这种方法是非科学的吗?因为它实在没有什么一定的方式,不但A,B,C,D在第二图可随意平分排在上下两排,而且还不一定要排在右边四个位置,只要你自己记清楚就好了。举个例说,譬如你第一次将钱收在手里的时候是这样一个顺序:A,B,E,F,G,H,C,D,你就可以排成第四图(样子很多,这里不过随便举出两种),无论在哪一种里,其目的总在把A,B,C,D平分成两排。同样的道理,第三图的变化也很多。
第四图
老实说,这种玩法简直无异于这样:你的两只手里各拿着四个钱,先问别人所要的在哪一只手,他若说“右”,你就将左手的甩掉,从右手分两个过去;再问他一次,他若说“左”,你又把右手的两个丢开,从左手分一个过去,再问他所要的在哪只手。朋友,你说可笑不可笑,你左手、右手都只有一个钱了,他对你说明在左在右,还用你猜吗?
所以第一种玩法是蒙混“侏儒”的小巧玩意儿。
现在来说第二种。
第五图
第六图
第二种和第一种的不同,就是钱的三次位置,别人是在最后一次才一口气说出来,这倒需有点儿硬功夫。我还是先将玩法叙述一下吧。第一次排成第五图的样子,其实就是第一图,“上下”指的是排数,“1,2……8”是钱的位置。你叫别人认定并且记好了上下,就将钱收起,照1,2,3,4,5,6,7,8的顺序收,不可弄乱。
收好以后你就从左到右先排下一排,后排上一排,成第六图的样子。
第七图
别人看好以后,你再照1,2,3,4,5……的次序收起,照同样的方法仍然从左到右先排下一排,再排上一排,这就成第七图的样子。
在这么一回,若他说出来的是“上下下”,那就是下一排的第二个;若他说“下下下”,那就是下一排的第四个。
为什么是这样呢?
朋友,因为摆成功是那样的,我们无妨将八个钱三次的位置都来看一下:
这样看起来,A,B,C,D……八个钱三次的位置没有一个相同,所以无论他说哪一个你都可以指出来。
朋友,这次你该明白了吧?不过你还不要太高兴,我这段“八仙过海指南”还没有完呢,而且所差的还是最重要的一个“秘诀”。你难道不会想A,B,C,D……这几个字只有这图上才有,平常的铜圆上没有吗?即使你另有八个记号,你要记清楚上上上是A,下下下是H……这样做也够辛苦的了。在这里却用得到“秘诀”。所谓秘诀就是八个中国字:“王、元、平、求、半、米、斗、非。”这八个字,马虎点儿说,都可分成三段,若某一段中含有一横那就算表示“上”,不是一横便表示“下”,所以王字是上上上,元字是上上下……我们可以将这八个字和第七图相对顺次排成第八图的样子:
第八图
由第八图,就可看明白,你只要记清楚王、元、平、求……的位置顺序和各字所代表的三次位置的变化,别人说出他的答案以后,你口中念念有词地暗数应当是第几个就行了。
譬如别人说下上上,那么应当是“半”字,在第五位;若他说上下上,应当是“平”字,在第三位,这不就可以瓮中捉鳖了吗?
暂时我们还不说到数学上面去。我且问你,这个玩意儿是不是限定要八个钱不能少也不能多?是的,为什么?假如不是,又为什么?“是”或“不是”很容易说出口,不过学科学的人第一要紧的是既然下个判断,就得说出理由来,除了对于那几个大家公认的基本公理或假说,是不容许乱说的。
经我这样板了面孔地问,朋友,你也有点儿踌躇了吧?大胆一点儿,先回答一个“是”字。真的,顾名思义,“八仙过海”当然总共要八个,不许多也不许少。
为什么?
因为分上下排,只排三次,位置的变化总共有八个,而且也只有八个。所以钱少了就有空位置,钱多了就有变化重复的。
怎样知道位置的变化总共有八个,而且只有八个呢?
不错,这是我们应当注意到的问题的核心,但是我现在还不能回答这个,且把问题再来盘弄一回。
“八仙过海”这玩意总共有下面的几个条件:
(1)八个钱;
(2)分上下两排摆;
(3)前后总共排三次;
(4)收钱的顺序是照直行由上而下,从第一行起[1];
(5)摆钱的顺序是照横排由左而右,从第一排起。
(4)(5)是排的步骤,(1)(2)(3)都直接和数学关联。前面已经回答过了,倘使(2)(3)不变,(1)的数目也不能变。那么,假如(2)或(3)改变一下,(1)的数目将怎样?
我简单地回答你,(1)的数目也就跟着要变。换句话说,若排数加多“(2)变”或是排的次数加多“(3)变”,所需要的钱就不只八个,不然便有空位要留出来。
先假定排成三排,那么我告诉你,就要二十七个钱,因为上、中、下三个位置三次可以调出二十七个花样。你不信吗?请看下图:
第九图
第十图
第十一图
第九图本来是任意摆的,不过为了说明方便,所以假定了一个从(1)到(27)的顺序。
从第九图,参照(4)(5)两步骤,就可摆成第十图。
从第十图,参照(4)(5)两步骤,就可摆成第十一图。
现在我们来猜了。
甲说“上中下”——他认定的是6;
乙说“中下上”——他看准的是16;
丙说“下上中”——他瞄着的是20;
丁说“中中中”——他注视的是14;
……
总共二十七个钱,无论别人看定的是哪一个,只要他没有把三次的位置记错或说错,都可以拿出来。
这更奇妙了,又有什么秘诀呢?
没有,没有,没有,回答三个“没有”或五个“没有”。“八仙过海”的秘诀不过比一定的法则来得灵动些,所以才用得着。现在要找二十七个字可以代表上、中、下的位置变化,实在没这般凑巧,即或有,记起来也一定不便当。那么,怎样找出别人认准的钱来呢?
好,你要想知道,那我们就来仔细考察第十一图,我将它画成第十二图的样子。
第十二图
图中分成三大段,你仔细看:第一段的九个是1到9,在第九图中,恰好都在上一排,所以我在它的下面写个大的“上”字;第二段的九个是10到18,在第九图中恰好都在中一排,所以下面写个大的“中”字;第三段的九个是从19-27,在第九图中恰好都是下一排,所以用一个大的“下”字指明白。
你再由各段中看第一行,它们在第十图中都是站在上一排;各段中的第二行,在第十图中都站在中一排;而各段的第三行,在第十图中都站在下一排。
这样,你总可明白了。甲说“上中下”,第一次是上,所以应当在第一段;第二次是中,所以应当在第一段的第二行;第三次是下,应当在第一段第二行的下一排,那不是6吗?
又如乙说“中下上”,第一次是中,应当在第二段;第二次是下,应当在第二段的第三行;第三次是上,应当在第二段第三行的上一排,那不就是16吗?
你再将丙、丁……所说的去检查看。
明白了这个法则的来源和结果,依样画葫芦,无论排几排都可以,肯定成功,而且找法也和三排的一样。例如我们排成四排,那就要六十四个钱,我只将图画在下面,供你参考。说明呢,不再重复了。至于五排、六排、十排、二十排都可照推,你无妨自己画几个图去看。
第十三图
第十四图
第十五图
譬如有人说“二四三”,那么他看定的钱在第十五图中的第二段第四行第三排,就是31;若他说“四三一”,那就应当在第十五图中的第四段第三行第一排,他所注视的是57。
上面讲的是排数增加,排的次数不变。现在假定排数不变,只是排的次数变更,再看有什么变化。我们就限定只有上下两行排。
第一步,譬如只排一次,那么这很清楚,只能用两个钱,三个就无法猜了。
若排两次呢,那就用四个钱,它的变化如下:
第十七图
第十六图
它的变化是:
三次就是“八仙过海”,不用再说。譬如排四次呢,那就用十六个钱,排法和上面说过的一样,变化的图如下:
第十八图
第十九图
第二十图
第二十一图
例如有人认定的钱的四次的位置是“上下下上”,那么应当在第二十一图中的第一段第二分段第二行的上排,是7;又如另有一个人说他认定的钱的位置是“下下上上”,那就应当在第二十一图中的第二段第二分段第一行的上一排,便是13。
照推下去,五次要用三十二个钱,六次要用六十四个钱……喜欢玩的朋友无妨当作消遣去试试看。
总结一下:前面说“八仙过海”的五个条件,由这些例子看起来,第一个是跟着第二、第三个变的。至于第四、第五,关于步骤的条件和前三个都没有什么直接关系。它们也可以变更。例如(4)我们也可以由下而上,或从末一行起,而(5)也可以由右而左从第一排起。不过这么一来,所得的最后结果形式稍有点儿不同。
从我们所举过的例子看,钱的数目是这样:
(1)分两排:
(a)排一次——2个
(b)排二次——4个
(c)排三次——8个
(d)排四次——16个
(2)分三排:
(a)排一次——3个(我们可以想得到的)
(b)排二次——?个(请你先想想看)
(c)排三次——27个
(d)排四次——?个
(4)分四排:
(a)排一次——4个(我们可以想得到的)
(b)排二次——?个
(c)排三次——64个
(d)排四次——?个
这次却真的到了底,我们要解决的问题是:
“分多少排,总共排若干次,究竟要多少钱,而且只能要多少钱?”
上面已举出的钱的数目,在那例中都是必要而且充足的,说得明白点,就是不能多也不能少。我们怎样回答上面的问题呢?假如你只要一个答案就满足,那么是这样的:
设排数是a,排的次数是x,钱数是y,这三个数的关系如下:
y=ax
我们将前面已讲的例代进去,看看这个话是否靠得住:
(1)(a)a=2,x=1,∴y=21=2
(b)a=2,x=2,∴y=22=4
(c)a=2,x=3,∴y=23=8
(d)a=2,x=4,∴y=24=16
(2)(a)a=3,x=1,∴y=31=3(www.chuimin.cn)
(b)a=3,x=2,∴y=32=9(对吗?)
(c)a=3,x=3,∴y=33=27
(d)a=3,x=4,∴y=34=81(?)
(3)(a)a=4,x=1,∴y=41=4
(b)a=4,x=2,∴y=42=16(?)
(c)a=4,x=3,∴y=43=64
(d)a=4,x=4,∴y=44=256(?)
照这个结果来看,我们所用过的例子都合得上,那个回答大概总有些可靠了。就是几个不曾试过的数,想起来也还不至于错误。不过单是这样还不行,别人总得问我们理由。此刻是无可拖延,只得找出理由来。
真要理由吗?就是将我们所用过的例子合在一起用脑力去想,一定可以想得出来的。不过,这实在大可不必,有别人的现成架子可以装得上去时,直接痛快地装上去多么爽气。那么,在数学中可以找到这一栏吗?
可以。那就是顺列法,我们就来说顺列法吧。
先说什么叫顺列法。
有几个不相同的东西,譬如A,B,C,D……几个字母,将它们的次序颠来倒去地排,计算这排法的数目,这种方法就叫顺列法。
第二十二图
顺列法的计算本来比较复杂,而且一不小心就容易弄错,要想弄清楚,自然只好去读教科书或是去请教你的数学教师。这里不过说着玩玩,只得限于基本的几个法则了。
第一,我们来讲几个东西全体的、不重复的顺列。这句话须得解释一下,譬如有A、B、C、D四个字母,我们一齐将它们拿出来排,这叫全体的顺列。所谓不重复是什么意思呢?那就是每个字母在一种排法中只需用一回,就好像甲、乙、丙、丁四个人排座位一样,甲既然坐了第一位,其余的三位当然不能再坐他的座位了。
要计算A、B、C、D这种排列法,我们先假定有四个位置在一条直线上,譬如是桌上画的四个位置,A、B、C、D是写在四个铜圆上的。
第一步我们来就第一个位置想,A、B、C、D四个钱全都没有排上去,所以无论我们用哪一种摆法都行。这就可以知道,第一个位置有4种排法。我们取一个钱放到了1,那就只剩三个位置和三个钱了,跟着来摆第二个位置。
外面剩的钱还有三个,第二个位置无论用这三个当中的哪一个去填它都是一样。这就可以知道,第二个位置有3种排法。到了第二个位置也有一个钱将它占领时,桌子上只剩两个位置,外边只剩两个钱了。
第三个位置因为只有两个钱剩在外面,所以填的方法也只有2个。
当第三个位置也被一个钱占领了时,桌上只有一个空位,外面只有一个闲钱,所以第四个位置的排法便只有1个。
为了一目了然,我们还是来画一个图。
第二十三图
仔细观察第二十三图第一位,无论是A、B、C、D四个当中的哪一个,A,或B,或C,或D,第二位都有三个排法,所以第一、第二位合在一起共有的排法是:
4×3
而第二位无论是A、B、C、D中的哪一个,第三位都有两个排法,所以一、二、三、四个位置连在一起算,总共的排法是:
4×3×2
至于第四位,跟着第三位已经定了,只有一个方法,因此第四个位置总共的排法是:
4×3×2×1=24
我们由图上去看,恰好总共是二十四排。
假如桌上有五个位置,外面有五个钱呢?那么第一个位置照前面说过的有5种排法,第一位排定以后,下面剩四个位置和四个钱,它们的排法便和前面说过的一样了,所以五个位置的钱的排法是:
5×4×3×2×1=120
前面是从1起连续的整数相乘一直乘到4,这里是从1起乘到5。假如有六个位置和六个钱,同样我们很容易知道是从1起将连续的整数相乘乘到6为止,就是:
6×5×4×3×2×1=720
譬如有八个人坐在一张八仙桌上吃饭,那么他们的坐法便有40320种,因为:
8×7×6×5×4×3×2×1=40320
你家请客常常碰到客人推让座位吗?真叫他们推来推去,要让完这40320种排法,从天亮到天黑也让不完呢。
一般的法则,假设位置是n个,钱也是n个,它们的排法便是:
n×(n-1)×(n-2)×……×5×4×3×2×1
这样写起来太不方便了,不是吗?在数学上,对于这种从1起到n为止的n个连续整数相乘的把戏,给它起一个名字叫“n的阶乘”,又用一个符号来代表它,就是n!,用式子写出来便是:
n的阶乘=n!=n×(n-1)×(n-2)×……×5×4×3×2×1
所以 8的阶乘=8!=8×7×6×5×4×3×2×1=40320
6的阶乘=6!=6×5×4×3×2×1=720
5的阶乘=5!=5×4×3×2×1=120
4的阶乘=4!=4×3×2×1=24
3的阶乘=3!=3×2×1=6
2的阶乘=2!=2×1=2
1的阶乘=1!=1
有了这个新的名词和新的符号,说起来就便当了!
“n个东西全体不重复的排列就等于n的阶乘n!。”
但在平常我们排列东西的时候,往往遇见位置少而东西多的情形。举个例说,譬如你有一位朋友,他运道来了,居然奉国民政府的命令去当什么县的县长。这时你跑去向他贺喜,这自然是值得贺的,不是吗?已升官就可发财了!但是当你看到他时,一眼就可以看出来,他的脸孔上直一条、横一条的喜纹当中也夹着正一条、歪一条的愁纹。你若问他愁什么,他定会告诉你,一个衙门里不过三个科长、六个科员、两个书记,荐人来的便签倒有三四十张,这实在难于安排。
真的,朋友,莫怪你的朋友难于安排,他想不得罪人简直不行!就算他只接到三十张荐人的便签,就算他的衙门里从科长数到洗马桶的总共要用三十个人,但是人全是两道眉毛横在两只眼睛上的,哪个会看得见自己的眉毛的粗细,哪个不想当第一科科长!倘使你的朋友请你替他安排,你左排也不是,右排仍然不是,你也只得在脸上挂起愁纹来了。三十个人排来排去有多少?我没有这样的闲工夫去算,你只要想,单是八的阶乘就已有40320了,那三十的阶乘将是多么大的一个数!
笔一滑,又说了一段空话,转到正文吧。
譬如你那朋友接到的便签当中只有十张是要当科长的,科长的位置总共是三个,有多少种排法呢?这就归到第二种的顺列法。
第二,我们来讲几个东西部分的、不重复的顺列法。因为粥少僧多,所以只有一部分人的便签有效。因为国民政府的命令兼差不兼薪,没有哪个人这般傻气,吃一个人的饭肯做两个人的事,所以排起来不重复。
从十张便签中抽出三个来,分担第一、第二、第三科的科长,这有多少法子呢?
朋友,你对于第一个法子若是真明白了,这一个是很容易的。第一科长没有定人时,十张便签都有同样的希望,所以这个位置的排法是10。
第一科长已被什么人得去了,只剩九个人来抢第二科的科长,所以第二个位置的排法是9。同一个道理第三个位置的排法是8,照第一种方法推来,这三个位置的排法总共应当是:
10×9×8=720
若是你的朋友接到的便签中间,想当科长的是十一个或九个,那么其排法就应当是:
11×10×9=990
或9×8×7=504
若是他的衙门里还有一个额外科长,总共有四个位置,那么他的安排应当是:
10×9×8×7=5040
11×10×9×8=7920
或9×8×7×6=3024
我们仍然用n代表东西的数目(在数学上算数的时候,朋友,你不必生气,人也只是一种东西,倒无关于他有没有当科长的福分),不过位置的数目既然和东西的不同,所以得另用一个字母来代表,譬如用n,我们的题目变成了这样:
“在n个东西里面取出m个来的排法。”
照前面的推论法,m个位置,n个东西,第一位的排法是n;第二个位置的排法,东西已少了一个,所以只有n-1;第三个位置,东西又少了一个,所以只有n-2个排法……照推下去,直到第m个位置,它的前面有m-1个位置,而每一个位置都拉了一个人去,所以被拉去的共有m-1个人,就总人数说,这时已少了m-1个,只剩n-(m-1)个了,所以这个位置的排法是n-(m-1)。
这样一来,总共的排法便是:
n×(n-1)×(n-2)×(n-3)……×[n-(m-1)]
比如n是11,m是4,代进去就得:
11×(11-1)×(11-2)×(11-3)=11×10×9×8=7920
在实际上只要从n写起,往下总共连着写n个就行了。
这种排法也有一个符号,就是nPm。P左边的n表示总共的个数,P右边的m表示取出来排的个数,所以如在26个字母当中取出5个来排,它的方法总共就是26P5[2]。
将上面的计算用这符号连起来,就得出下面的关系:
这里有一件很有趣味的事,譬如我们将前面说过的第一种排法也用这里的符号来表示,那就成为nPn,所以:
在n个东西当中去了m个,剩的还有n-m个,这n-m个若自己掉来掉去地排,它的数目就应当是:
朋友,我问你,用(n-m)!去除n!得什么?
如果你们想不出,我就将它们写出来:
从这个式子一看分子和分母将公因数消去后,恰好得:
这式子的右边和(1)式的完全一样,所以:
这个式子很有意思,我们可以这样想:从n个当中取出m个来排,和将n个全排好,从第m+1个起截断一样,因为nPn是n个的排列,n-mPn-m是m个以后所余的东西的排列。
举个例来说,5个字母取出3个来的排法是5P3,而5-3=2,
关于这两种顺列法的计算,基本原理就是这样。但应用起来却不容易,因为许多题目往往包含着一些特殊条件,它们所能排成功的数目就会减少。譬如八个人坐的是圆桌,大家预先又没有说明什么叫首座,这比他们坐八仙桌的变化就少得多。又譬如在八个人当中有两个是夫妻,非挨着坐不可,或是有两个是生冤家死对头,不能坐在一起,或是有一个人是左手拿筷子的,若坐在别人的右边不免要和别人的筷子冲突起来。这些条件是数不尽的,只要有一个存在,排列的数目就得减少。朋友,你要想详细知道,我只好劝你去读教科书或去请教你的教师,这里却不谈了。
呵!你也许不免要急得跳起来了吧?说了半天,和“八仙过海”有什么关系呢?这是应当赶快解决的,不错。但还得请你忍耐一下,单是这样,这架子还不够,不能好好地将“八仙过海”这一类的玩意儿往上摆。我们得另说一种别的排列法。
前面的两种都是不重复的,但“八仙过海”每一个钱的三次位置不是上就是下,所以总得重复,这种排列法究竟和前面所说过的两种有点儿大同小异,就算它是第一种吧。
第三种是n种东西m次数可重复的顺列。就用“八仙过海”来作例,排来排去,不是上便是下,所以就算有两种东西,我们无妨用a、b来代表它们。
第二十四图
首先说两次的排法,就和第二十四图一样。第一个位置因为我们只有a、b两种不同的东西,所以只好有2种排法。
但是在这里,因为a和b都可重用的缘故,就是第一个位置被a占了,它还是可以有2个排法;同样地,它被b占了也仍然有2个排法。因此总共的排法应当是:
第二十五图
譬如像“八仙过海”一般,排的是3次呢,照这里的话说,就是有三个位子可排,那么就如第二十五图的样,全体的排法是:
2×2×2=23=8
这不就说明了“八仙过海”,分上下两排,总共排三次,位置不同的变化是8吗?
第二十六图
我们前面曾经说过分三排只排三次的例子,用a,b,c代表上、中、下,说明是一样的,暂且省略。就第二十六图看,可以知道排列的总方法是:
3×3×3=33=27
这个数目和我们前面所用的钱恰好一样。
照同样的例子,分一、二、三、四,四排只排三次的数目是:
4×4×4=43=64
第二十七图
前面还说过排数不变、次数变的例子。两排只排三次,已说过了。两排排四次呢,那就如第二十七图,总共能排的数目应当是:
2×2×2×2=24=16
若排的是三排,总共排四次,照同样的道理,它的总数是:
3×3×3×3=34=81
以前所举出的例子都可照样推算出来。将这几个式子在一起比较,乘数是跟着排数变的,乘的次数,就是指数,是跟着排的次数变的,所以若排数是a,排的次数是x,钱数是y,那么,
y=ax
用一般的话来说,就是这样:
“n种东西,m次数可重复的顺列,便是n的m次乘方,nm。”
所谓“八仙过海”,现在可算明白了,不过是顺列法中的一种游戏,有什么奇妙呢?你只要记好y等于a的x乘方这个式子,你想分几排,排几次,心里一算就可知道,应当请几位神仙下凡。你再照前面所说过的(4)(5)两个步骤去做,神仙的道法虽高,如来佛的手心却可伸缩,岂知孙悟空的筋斗云无用呢?
【注释】
[1]编者注:作者生活的年代的“行”的意思相当于现代的“列”,数数规则是从右往左数,也与现代不同。
[2]编者注:现代表示法为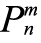 。
。
有关原来数学这样有趣的文章

数学面貌的大变化对数学教育提出了新的要求。改革数学教育的浪潮,席卷了世界所有发达国家。数学教育已经成为一门受到广泛重视的学科。数学教育学的对象是数学教学,而不是数学本身。于是,数学教育学要靠数学提供材料。为了数学教育的需要,对数学成果进行再创造,这已不是数学教育学的任务了。这主要是数学工作者的责任,是数学的任务。......
2023-10-17

为底的对数——自然对数。若用曲线y=下的面积引入自然对数lnx,则显得简单具体、直观性强,而且涉及的基础知识少,还把平面几何、解析几何与高等数学更密切地联系起来了。推论6.3.3对任意λ>0,有①也可不用压缩变换,直接用求导方法证明sx1=sλxλ。至此,可以引入自然对数了。定义6.3.2对0<x<+∞,记=lnx,并称函数y=lnx为x的自然对数。从两个定义及三个推论中,立刻得到自然对数的一系列性质。......
2023-10-17

之所以说十进制并非尽善尽美,我们有更有力的理由:因为还有比十进制记数法更优越的方法。充分利用这5个指头,能造出更好的记数法来。这种记数法的好处,不仅在于少用了6,7,8,9这4个数码,更重要的是运算起来方便。比方说,3.68在新记数法里是,截尾之后得到,恰好是3.7,相当于把3.68最后的8进上去。可见,十进制记数法虽然是一份珍贵的遗产,同时也是沉重的负担。因为世界上已经有太多的人学会了现在通行的十进制记数法。......
2023-10-17

有了连续归纳法,数学分析里的一系列涉及实数连续性和连续函数性质的定理,就可以用统一的模式来证明。以下用连续归纳法证明:这将推出每个实数都是{bn}的下界,即得矛盾。由连续归纳法,px对一切x成立。[例8.3.6]设f在[a,b]上连续,f<0,f>0,则至少有一个点x0∈(a,b),使f=0。[例8.3.7]若f在[a,b]上连续,则f在[a,b]上取到最大值和最小值。......
2023-10-17

既然讲数列极限可以不用“ε-语言”,那么讲函数极限也可以不用“ε-语言”,只不过用“无界不减函数”代替“无界不减数列”罢了。定义7.4.2设f是在[c,+∞)上有定义的函数。用“ε-语言”讲函数极限,常常要一条一条分别给出各种过程中的极限定义。这一套定义,将使学生在学习微积分时免受“ε-语言”之累,在定理证明和做题时用代数运算代替逻辑推理。[例7.4.1]求证:=+∞。......
2023-10-17

定义7.3.3设{an}是无穷数列。用“ε-语言”,不仅能够引入极限概念,还能证明与极限有关的一系列基本定理,直接计算一些具体的极限。实践证明确实有效,而且比用“ε-语言”还要简便![例7.3.1]求证数列是无穷小列。有些微积分的参考资料以此题为例,说明不用“ε-语言”不可能严格地讲微积分。命题7.3.1设{αn}、{βn}为无穷小列,{Ln}为有界数列。......
2023-10-17

命题5.4.1设M、N两点在直线AB的同侧,则MN∥AB的充分必要条件是△MAB=△MAB。这是上一小节已证明的例题5.3.9。命题5.4.2两直线AB、CD和另一直线l交于P、Q,若同位角相等,则AB∥CD。于是,共角比例定理可以完善成为命题5.4.4若△ABC与△A′B′C′中,有∠A=∠A′或∠A+∠A′=180°,则。命题5.4.5PQ∥AB,若直线l与AB垂直,则l也和PQ垂直。推论5.4.2平行线处处等距。推论5.4.3若直线l1∥l2,而l3与l1、l2相截,则内错角相等。......
2023-10-17

写稿要找题目,不很容易,这次就可以用联而且想之法,由汽车而扩大,说“代步”;又泛论不好写,只说自己的一点点经历和感受。《水浒传》里有神行太保,可证找代步是无能。总之,思路随道家,对不用腿而找代步就不会有什么好印象。表现于代步方面,有轨变为无轨,长亭短亭变为高速,余落日的渡头变为机场。不只文章,情意也是自己的特别值得珍重,所以就本诸存诚的原则,以下说说与代步有关的或说由代步引起的情意。......
2023-07-30
相关推荐