在新批评的认识中,文学与科学的差异认识是新批评对诗歌在理性与感性,思想与情感统一认识层面的主要论点。具体而言,首先,文学与科学有着不同的话语特征。另外,新批评还认为,因为科学话语不需要感性和理性的辩证统一,而只力求以简洁的方式来表现事实,所以诗歌形成过程中最重要的张力因素在科学话语中是不存在的。新批评对于文学与科学的区分有时候还被表述为文学与散文的区分。......
2024-01-19
这里所要说明的“数学”这一个词,包含着算术、代数、几何、三角等等在内。用英文名词来说,那就是Mathematics。它的定义,照平常的想法,非常简单、明了,几乎用不到再说明。若真要说明,问题却有很多。且先举罗素(Russell),在他所著的《数理哲学》提出的定义,真是叫人莫名其妙,好像在开玩笑一样。他说:
“Mathematics is the subject in which we never know what we are talking about nor whether what we are saying is true.”
将这句话粗疏地翻译出来,就是:
“数学是这样一回事,研究它这种玩意儿的人也不知道自己究竟在干些什么。”
这样的定义,它的惝恍迷离,它的神奇莫测,真是“不说还明白,一说反糊涂”。然而,要将已经发展到现在的数学的领域统括得完全,要将它繁复、灿烂的内容表示得活跃,好像除了这样也没有别的更好的话可说了。所以伯比里慈(Papperitz)、伊特耳生(Itelson)和路易·古度拉特(Louis Couturat)几位先生对于数学所下的定义也是和这个气味相同。
对于一般的数学读者,这定义,恐怕反而使大家坠入五里雾中,因此拨云雾见青天的工作似乎少不了。罗素所下的定义,它的价值在什么地方呢?它所指示的是什么呢?要回答这些问题,还是用数学的其他定义来相比较更容易明白。
在希腊,亚里士多德(Aristotle)那个时代,不用说,数学的发展还很幼稚,领域也极狭小,所以只需说数学的定义是一种“计量的科学”,便可使人心满意足了。可不是吗?这个定义,初学数学的人是极容易明白、满足的。他们解四则问题、学复名数的计算,再进到比例、利息,无一件不是在计算量。就是学到代数、几何、三角,也还不容易发现这个定义的破绽。然而仔细一想,它实在有些不妥帖。第一,什么叫作量,虽然我们可以用一般的知识来解释,但真要将它的内涵弄明白,也不容易。因此用它来解释别的名词,依然不能将那名词的概念明了地表示出来。第二,就是用一般的知识来解释量,所谓计量的科学这个谓语也不能够明确地划定数学的领域。像测量、统计这些学科,虽然它们各有特殊的目的,但也只是一种计量。由此可知,仅仅用“计算的科学”这一个谓语联系到数学而成一个数学的定义,未免广泛了一点。
若进一步去探究,这个定义的欠缺还不止这两点,所以孔德(Comte)就加以修改而说:“数学是间接测量的科学。”照前面的定义,数学是计量的科学,那么必定要有量才有可计算的,但它所计的量是用什么手段得来的呢?用一把尺子就可以量一块布有几尺几寸宽、几丈几尺长;用一杆秤就可以量一袋米有几斤几两重,这自然是可以直接办到的。但若是测量行星轨道的广狭、行星的体积,或是很小的分子的体积,这些就不是人力所能直接测定的,然而由数学的方法可以间接将它们计算出来。因此,孔德所下的这个定义,虽然不能将前一个定义的缺点完全补正,但总是较进一步了。
孔德究竟是十九世纪前半期的人物,虽然他是一个不可多得的哲学家和数学家,但在他的时代,数学的领域远不及现在广阔,如群论、位置解析、投影几何、数论以及逻辑的代数等,这些数学的支流的发展,都是他以后的事。而这些支流和量或测量实在没什么关系。即如笛沙格(Desargues)所证明的一个极有兴味的定理:“两三角形的顶点若在集交于一点的三直线上,则它们的相应边的交点就在一条直线上。”
这个定理的证明,就只用到位置的关系,和量毫不相干。数学的这种进展,自然是轻巧地将孔德所给的定义攻破了。
到了1970年,皮尔士(Peirce)就另外给数学下了一个这样的定义:
“数学是产生‘必要的’结论的科学。”
不用说,这个定义比以前的都广泛得多,它已离开了数、量、测量等这些名词。我们知道,数学的基础是建筑在几个所谓公理上面的。从方法上说,不过由这几个公理出发,逐渐演绎出去而组成一个秩序井然的系统。所谓公式、定理,只是这演绎所得的结论。
照这般说法,皮尔士的定义可以说是完整无缺吗?
不!依了几个基本的公理,照逻辑的法则演绎出的结论,只是“必然的”。若说是“必要”,那就很可怀疑。我们若要问怎样的结论才是必要的,这岂不是很难回答吗?
更进一步说,现在的数学领域里面,固然大部分还是采用着老方法,但像皮亚诺(Peano)、布尔(Boole)和罗素这些先生们,却又走着一条相反的途径,对于数学的基础的研究他们要掉一个方向去下寻根问底的工夫。
于是,这个新鲜的定义又免不了摇动。
关于这定义的改正,我们可以举出康伯(Kempe)的来看,他说:
“数学是一种这样的科学,我们用它来研究思想的题材的性质的。而这里所说的思想,是归依到含着相异和相同,个别和复合的一个数的概念上面。”
这个定义,实在太严肃、太文气了,而且意味也有点儿含混。在康伯以后,布契(Bôcher)把它改变了一下,便这样说:
“倘若有某一群的事件与某一群的关系,而我们所要研究的问题,又单只是这些事件是否适合于这些关系,这种研究便称为数学。”
在这个定义中,有一点最值得注意,布契提出了“关系”这一个词来解释数学,它并不用数咧、量咧这些家伙,因此很巧妙地将数学的范围扩张到“计算”以外。
假如我们只照惯用的意义来解释“计算”,那么,到了现在,数学中有些部分确实和计算没有什么因缘。
也就因为这个缘故,我喜欢用“数学”这个词来译Mathematics,而不喜欢用“算学”。虽然“数”字也还不免有些语病,但似乎比“算”字来得轻些。
倘使我们再追寻一番,我们还可以发现布契的定义也并不是“悬诸国门不能增损一字”的。不过这种功夫越来越细微,也不容易理解。而我这篇东西不过想给一般的数学读者一点儿数学的概念,所以不再往里面穷追了。
将这个定义来和罗素所下的比较,虽然距离较近,但总还是旨趣悬殊。那么,罗素的定义果真是开玩笑吗?
我是很愿意接受罗素的定义的,为了要将它说得明白些,也就是要将数学的定义——性质——说得明白些,我想这样说:
“数学只是一种符号的游戏。”
假如,有人觉得这样太轻佻了一点儿,严严正正的科学怎么能说它是“游戏”呢?那么,这般说也可以:
“数学是使用符号来研究‘关系’的科学。”(www.chuimin.cn)
对于数学这种东西,读者大都有过这样的疑问,这有什么意思呢?这有什么用呢?本来它不过让你知道一些关系,以及从某种关系中推演出别的关系来,而关系的表出大部分又只靠着符号,这自然不能具体地给出什么用场和意义了。
为了解释明白上面提出的定义,我想从数学中举些例子来讲,更方便些。
一开头我们就看“一加二等于三”。
在这一个短短的句子里,照句子法上的说法,总共是五个词:“一”“二”“三”“加”“等于”。这五个词,前三个是一类,后两个又是一类。什么叫“一”?什么叫“二”?什么叫“三”?这实在不容易解答。它们都是数,数是抽象的,不是吗?我们能够拿一个铜板、一支铅笔、一个墨水瓶给人家看,但我们拿不出“一”来,“一”是一个铜板、一支铅笔、一个墨水瓶。一个这样,一个那样,这些的共相。从这些东西我们认识出这共相,要自己保存,又要传给别人,不得不给它起一个称呼,于是就叫它是“一”。我为什么叫“薰宇”,倘若你要问我,我也回答不上来,我只能说,这只是一个符号,有了它方便你们称呼我,让你们在茶余酒后要和朋友们批评我、骂我时,说起来方便些,所以“薰宇”两个字是我的符号。同样地,“一”就是一个铜板、一支铅笔、一个墨水瓶……这些东西的共相的符号。这么一说,自然“二”和“三”也一样只是符号。
至于“加”和“等于”在根源上要说它们只是符号,一样也可以,不过从表面上说,它们表示一种关系。所谓“一加二”是表示“一”和“二”这两个符号在这里的关系是相合;所谓“等于”是表示在它前后的两件东西在量上相同。所以归根到底“一加二等于三”只是三个符号和两个关系的联缀。
单只这么一个例子,似乎还不能够说明白。再举别的例子吧,假定你是将代数学完了的,我们就可以从数的范围的逐渐扩大来说明。
在算术里我们用的只是1,2,3,4……这些数,最初跨进代数的门槛,遇到a,b,c,x,y,z,总有些不习惯。你对于二加三等于五,并不惊奇,并不怀疑;对于二个加三个等于五个,也不惊奇,也不怀疑;但对于2a+3a=5a你却怔住了,常常觉得不安心,不知道你在干什么?其实呢,2a+3a=5a和2+3=5对于你的习惯来说,后者不过更像符号而已。有了这一个使用符号的进步,许多关系来得更简单、更普遍,不是吗?若是将2a+3a=5a具体化,认为a是一只狗的符号,那么这关系所表示的便是两只狗碰到了三只狗成为五只狗;若a是一个鼻头的符号,那么,这关系所表示的便是两个鼻头添上三个鼻头总共就成了五个鼻头。
再掉转一个方向来看,在算术中除法常有除不尽的时候,比如2÷3。遇见这样的场合,我们便有几种方法表示:
(1)2÷3=0.667弱
(2)2÷3=0.6……2
(3)2÷3=0.6
(4)2÷3=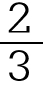
第一种只是一个近似的表示法;第二种表示得虽正确,但用起来不方便;第三种是循环小数,关于循环小数的计算,那种苦头你总尝到过;第四种是分数,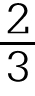 是什么?你已知道就是3除2的意思。对了,只是“意思”,毕竟没有除。这和3除6得2的意味终是不同的。所谓“意思”便是“符号”。因为除法有除不尽的时候,所以我们使用“分数”这种符号。有了这种符号,于是我们就可以推究出分数中的各种关系。
是什么?你已知道就是3除2的意思。对了,只是“意思”,毕竟没有除。这和3除6得2的意味终是不同的。所谓“意思”便是“符号”。因为除法有除不尽的时候,所以我们使用“分数”这种符号。有了这种符号,于是我们就可以推究出分数中的各种关系。
在算术里你知道5-3=2,但要碰到3-5你就没办法,只好说一句“不能够”。“不能够”?这是什么意思?我替你解释便是没有办法表示这个关系。但是到了代数里面,为了探究一些更普遍的关系,不能不想一个方法来突破这个困难。于是有些人便这样想,3-5为什么不能够呢?他们异口同声地回答,因为还差2的缘故。这一回答,关系就成立了,“从3减去5差2”。在这个当儿又用一个符号“-2”来表示“差2”,于是这关系就成为3-5=-2。这一来,真是“功不在禹下”。有了负数,我们一则可探讨它自身所包含的一些关系,二则可以将我们已得到的一些关系更普遍化。
又如在乘法中,有时只是一些相同的数在相乘,便给它一种符号,譬如a×a×a×a×a写成a5。这么一来,关于这一类的东西又有许多关系可以发现了,例如:
an·am=an+m
(an)m=anm
……
不但这样,这里的n和m还只是正整数,后来却扩张到负数和分数去而得出下面的符号:
这些符号的使用,是代数所给的便利,学过代数的人都已经知道了,我也不用再说了。
由整数到分数,由正整数到负数,由乘方到使用指数,我们可以看出许多符号的创立和许多关系的产生、繁殖。要将乘方还原,用的是开方,但开方常常会碰钉子,因此就有了无理数,如,√2,![]() ……这不过是一些符号,这些符号经过一番探索,便和乘方所用的指数符号结了很亲密的关系。
……这不过是一些符号,这些符号经过一番探索,便和乘方所用的指数符号结了很亲密的关系。
总结这些例子来看,除了使用符号和发现关系以外,数学实在没有什么别的花头。倘若你已学过平面三角,那么,我相信你更容易承认这句话。所谓平面三角,不就是只靠着几个什么正弦、余弦这类的符号来表示几个比,然后去研究这些比的关系和三角形中的其他关系吗?
我说“数学是使用符号来研究‘关系’的科学”,你应该不至于再怀疑了吧?
在数学中,你会碰到一些实际的问题要你计算,譬如三个十两五钱总共是多少斤。但这只是我们所得的关系的具体化,换句话说,不过是一种应用。
也许你还有一个疑问,数学中的公式和定理固然只是一些“关系”的表现形式,但像定义那类的东西又是什么呢?我的回答是这样,那只是符号的规定。“到一个定点距离相等的一个完全的曲线叫圆”。这是一个定义,但也只是“圆”这个符号的规定。
正正经经地说,数学只是这么一回事,但我仍然高兴地说它是符号的游戏。所谓“游戏”自然不是开玩笑的意思。两个要好的朋友拿着球拍在球场上打网球,并没有什么争胜的要求,然而兴致淋漓,不忍释手,在这时他们得到一种满足,这就是使他们忘却一切的原因,这叫游戏。小孩子独自拿着两块石子在地上造房子,尽管满头大汗,气喘不止,但仍然拼尽全身力气去做,这是游戏。至于为银盾而赛球,为锦标而练习赛跑,这便不是游戏了。还有为了排遣寂寞,约几个人打麻将、喝老酒,这也算不来游戏。就在这意味上,我说“数学是符号的游戏”。
自然,从这游戏中可有些收获——发现一些可以供人使用的关系。但符号使用得越多,所得的关系越不容易具体化。踏到数学的领域的后部,真的,你只见到符号和关系,那些符号、那些关系要说你个明白,就是马马虎虎地说,你也无从下手。
到这一步,好了,罗素便说:
“数学是这样一回事,研究它这种玩意儿的人也不知道自己究竟在干些什么。”
有关原来数学这样有趣的文章

在新批评的认识中,文学与科学的差异认识是新批评对诗歌在理性与感性,思想与情感统一认识层面的主要论点。具体而言,首先,文学与科学有着不同的话语特征。另外,新批评还认为,因为科学话语不需要感性和理性的辩证统一,而只力求以简洁的方式来表现事实,所以诗歌形成过程中最重要的张力因素在科学话语中是不存在的。新批评对于文学与科学的区分有时候还被表述为文学与散文的区分。......
2024-01-19

LED灯箱的制作材料① 外框:一般用铝合金型材制作。下面以1.5m×0.5m的四个字的灯箱为例来计算LED的数量。⑤ LED的选用和安装。LED质量直接影响灯箱的亮度,因此LED灯箱应选用高亮或者超高亮LED,发光角度为30°~45°。由电源功率计算LED的数量:N=P电源功率/PLED功率 (7-1)注意:LED功率是指LED的耗散功率。......
2023-06-15

科学是有确凿根据的知识,并无丝毫是无稽之谈,所以一切科学的知识都是通过证明的。可是有些真实的判断,其真实性是明显的,而又有些真实的判断其真实性不是一望而知,有待于证明的。证明则必须有根据,但常常作为证明的根据的又须证明,一直往后推到无须证明的真理,这就是明显的真理。在说服他人时,证明就须从他承认为明显的真理开始。这是教学中和作一般报告时所应注意的。......
2023-11-08

过去,人们,尤其是学习自然科学的人们,常说科学研究始于实验和观察,这是逻辑实证主义的观点。问题是科学研究的起点和动力,没有目的和计划的实验和观察实际上并不存在,即使存在也只能是科学研究的准备阶段。问题能力是文明水平的标志之一,是整体科学精神、科学态度和科学状况的反映。问题意识的普遍缺乏,与我国长期的教育制度、人才制度、研究制度有关,与我国国民的民主和法制意识有关。......
2023-08-13

因此,单靠弄清各组织如何组成复杂的机体,还不能够解答生命之谜,我们必须搞清楚各机体中的组织在根本上是如何由一个个不可分的单元组成的。一般的植物和动物都由极多个细胞组成,例如,一个成年人就是由几百万亿个细胞组成的。与由单个细胞组成的复杂机体一样,不用说也都具有“吃”“长”“生”这三种能力。......
2023-08-05

第21章蜜月之后爱情是理想,婚姻才是现实。现在该怎么办:好几种选择:1.召集团队成员,把项目真实的情况向他们摊牌。发布产品,反复改进使之完善。举例来说,苹果公司目前的媒体口碑很好,因为它的顾客们太满意了。如果苹果公司的顾客不满意,那媒体会像一群饿狼一样攻击苹果公司。......
2023-12-02

V=qv(1+η)tn式中 V——保护气体体积;qv——保护气体体积流量;t——单件焊接基本时间;n——每年、每月或每周焊件数量;η——气体损耗系数。例5:CO2气体保护焊,板厚δ=2mm,对接焊接过程中气体体积流量qv=8L/min,每件需焊5min,共10件。当η=0.04时,完成这批焊件所需CO2气体为多少?解:V=qv(1+η)tn=8××5×10L=416L答:需要CO2气体416L。已知:Q=12L/min;t=80min;n=15000;η=0.04解:V=qv(1+η)tn=12××80×15000L=14976000L又40L氩气在15MPa下,V1=6000L故答:需40L瓶装氩气2496瓶。......
2023-06-15

再如,秘书科的小李在接到一家客户的生意电报之后,立即向经理作了汇报。莫名其妙的小李本想向经理申辩两句,表示自己已经向他作了及时的汇报,只是当时他在谈话给忘了。这更是弄得小李糊涂不解。听了老赵的话,小李更是丈二和尚摸不着头脑,弄不清其中的奥秘。所以,经理的发怒与其说是针对小李,还不如说是给全公司听的。但是,如果小李不明事理,反而据理力争,这样,不仅不会得到经理的承认,而且很可能因此而被解雇。......
2023-12-06
相关推荐