以“结构体—基础”的现场装配为例具体说明,如图4-30所示。表4-15装配阶段——“基础”的BIM明细表清单1、数量清单2资料来源:作者自绘。完整的“可移动铝合金住宅产品”装配阶段的BIM明细表清单参见附录五。表4-17吊装、装配连接碳排放比例关系统计资料来源:作者自绘。......
2023-10-09
数据仓库是进行决策分析的基础,因此需要有强有力的工具来辅助管理决策者进行分析和决策。
在实际决策过程中,决策者需要的数据往往不是某一指标单一的值,他们希望能从多个角度观察某一指标或多个指标的值,并且找出这些指标之间的关系。比如,决策者可能想知道“东部地区和西部地区今年6月份和去年6月份在销售总额上的对比情况,并且销售额按10万~20万、20万~30万、30万~40万,以及40万以上分组”。决策所需的数据总是与一些统计指标(如销售总额)、观察角度(如销售区域、时间)以及级别(如地区、统计值区间划分)的统计(或合并)有关,我们将这些观察数据的角度称为维。可以说决策数据是多维数据,多维数据分析是决策的主要依据。但传统的关系数据库系统及查询工具对于管理和应用这样复杂的数据显得力不从心。
联机分析处理(OLAP)是专门为支持复杂的分析操作而设计的,它侧重于决策人员和高层管理人员的决策支持,可以满足分析人员的要求快速、灵活地进行大数据量的复杂查询,并且以一种直观易懂的形式将查询结果提供给决策人员,以便他们准确掌握企业(公司)的经营状况,了解市场需求,制订正确方案,增加效益。
OLAP是以数据库或数据仓库为基础,其最终的数据来源与OLTP一样均来自底层的数据库系统,但二者面向的用户不同,数据的特点与处理也明显不同。
OLAP与OLTP是两类不同的应用,OLTP面向的是操作人员和底层管理人员,OLAP面向的是决策人员和高层管理人员;OLTP是对基本数据的查询和增、删、改操作处理,它以数据库为基础,而OLAP更适合以数据仓库为基础的数据分析处理。OLAP所依赖的历史的、导出的及经综合提炼的数据均来自OLTP所依赖的底层数据库。OLAP数据较之OLTP数据要多一步数据多维化或综合处理的操作。例如,对一些统计数据,应首先进行预综合处理,建立不同级别的统计数据,从而满足快速统计分析和查询的要求。除了数据及处理上的不同之外,OLAP的前端产品和界面风格及数据访问方式也同OLTP不同,OLAP多采用便于非数据处理专业人员理解的方式(如多维报表、统计图形),查询及数据输出更直观灵活,用户可以方便地进行逐层细化及切片、切块、旋转等操作。而OLTP多为操作人员经常用到的固定表格,其查询及数据显示也比较固定、规范。
OLAP的基本概念包括如下内容。
(1)度量属性。
度量属性是决策者所关心的具有实际意义的数量。例如,销售量、库存量等。
(2)维度
维度(或简称为维)是人们观察数据的角度。例如,企业常常关心产品销售数据随着时间推移而产生的变化情况,这时企业从时间的角度来观察产品的销售,所以时间就是一个维(时间维)。企业也时常关心自己的产品在不同地区的销售情况,所以地理分布也是一个维(地理维)。如图9-3所示的多维分析示例中有三个维度:时间、商品类别和地区。

图9—3 多维数据分析
(3)维的层次
人们观察数据的角度(即某个维)还可以存在细节程度不同的多个描述方面,我们称这多个描述方面为维的层次。一个维往往具有多个层次,如描述时间维时,可以从日期、季度、月份、年等不同层次来描述,那么日期、月份、季度、年等就是时间维的层次;同样,城市、地区、国家就构成了地理维的多个层次。
(4)维度成员
维度的一个取值称为该维的一个维度成员。如果一个维是多层次的,那么该维的维度成员是在不同维层次的取值的组合。例如,我们考虑时间维具有日期、月份、年这3个层次,分别在日期、月份、年上各取一个值组合起来,就得到了时间维的一个维度成员,即“某年某月某日”。一个维度成员并不一定在每个维层次上都要取值,例如图9-3中的上半年、下半年等就是时间维的维度成员。
(5)多维数组
一个多维数组可以表示为:(维1,维2,……,维n,变量)。例如,如图9-3所示的商品的销售数据是按地理位置、时间和商品类别组织起来的三维立方体,加上变量“销售数量”,就组成了一个多维(地区、时间、商品类别、销售量)数组。
多维数组的取值称为数据单元。当多维数组的各个维都选中一个维度成员,这些维度成员的组合就唯一确定了度量属性的一个值。那么数据单元就可以表示为:(维1维度成员,维2维度成员,……维n维度成员,变量的值)。例如,在图9-3的地区、时间和商品类别维上各取维度成员“江苏”“第二季度”和“家电”,就唯一确定了度量属性“销售量”的一个值(图中为2443),则该数据单元可表示为:(江苏,第二季度,家电,2443)。
OLAP支持管理决策人员对数据进行深入观察,多维分析。多维分析是指对以多维形式组织起来的数据采取切片、切块、旋转等各种分析动作,以求剖析数据,使分析者、决策者能从多个角度、多个侧面观察数据库中的数据,从而深入地了解包含在数据中的信息、内涵。
联机分析处理系统通常包括以下基本的分析功能:
①上卷(roll-up)。上卷是在数据立方体中执行聚集操作,通过在维层次中上升或通过消除某个或某些维来观察更概况的数据。例如,如图9-4所示的数据立方体(水平轴为商品类别维,垂直轴为时间维,Z轴为地点维)经过沿着地点维的概念层次上卷,由城市上升到地区,就得到了如图9-5所示的立方体。现在销售量不是按照城市分组求值了,而是按照地区分组求值。(www.chuimin.cn)
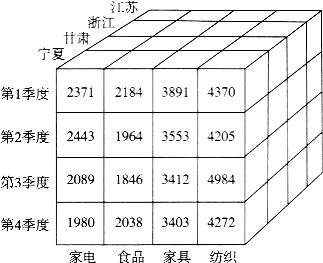
图9—4 数据立方体
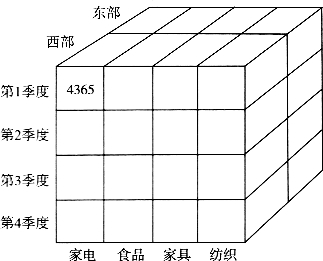
图9—5 图9—4上卷的效果
也可以通过消除一个或多个维来观察更加概括的数据。例如,如图9-6所示的二维立方体就是通过从图9-6的三维立方体中消除了“地区”维后得到的结果,这是将所有地区的销售数据都累计在一起。
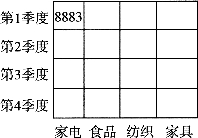
图9—6 消除“地区”维后的结果
②下钻(drilldown)。下钻是通过在维层次中下降或通过引入某个或某些维来更细致的观察数据。
例如,对如图9-4所示的数据立方体沿时间维进行下钻,由季度下降到月,就得到了如图9-7所示的数据立方体。现在的销售数量不是按季度计算,而是按月进行计算。
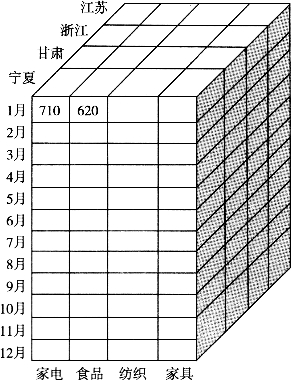
图9—7 图9—4下钻后的结果
③切片(slice)。切片是在给定的数据立方体的一个维上进行的选择操作,切片的结果是得到了一个二维的平面数据。
例如,在如图9-4所示的数据立方体上,使用条件“时间=1季度”进行选择,就相当于在原来的立方体中切出一片,结果如图9-8所示。
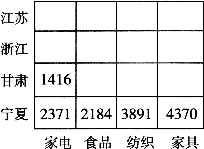
图9—8 图9—4切片后的结果
④切块(dice)。切块是在给定的数据立方体的两个或多个维上进行的选择操作,切块的结果得到了一个子立方体。进行选择时,相当于在原立方体中切出一小块,结果如图9-9所示。

图9—9 图9—4切片后的结果
⑤转轴(pivot or rotate)。转轴就是改变维的方向,将一个三维立方体转变为一系列二维平面。
例如,如图9-10所示的是图9-8的二维切片的“商品类别轴”和“地区轴”交换位置的结果。
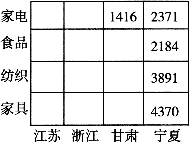
图9—10 图9—8转轴后的结果
有关数据库技术与应用教程的文章

以“结构体—基础”的现场装配为例具体说明,如图4-30所示。表4-15装配阶段——“基础”的BIM明细表清单1、数量清单2资料来源:作者自绘。完整的“可移动铝合金住宅产品”装配阶段的BIM明细表清单参见附录五。表4-17吊装、装配连接碳排放比例关系统计资料来源:作者自绘。......
2023-10-09

查询分析可以对确定无法进一步处理的规范化查询予以拒绝,拒绝的主要原因是该查询的变量类型是不正确的,或者语义是不正确的,等等。 假设有三个关系,分别是Student(学生)、COURSE(课程)和SC,我们来看下面的SQL查询:Select sname,cnof rom Student,SC,COURSEwhere Student.sno=SC.sno AND cname="CAD/CAM"AND age=23图7.1为了对应例7.2的查询图,分为两个不相连的子图。拒绝该查询,或者假设存在一个蕴含SC和COURSE的连接或笛卡儿积运算。图7.1不相连的查询图......
2023-10-28

OLTP旨在处理同时输入的成百上千的事务。从功能角度来看,OLTP负责基本业务的正常运转;而业务数据积累时所产生的价值信息则被OLAP不断呈现出来,企业/管理高层通过参考这些信息会不断地调整经营/管理方针,也会促进基础业务的不断优化,这是OLTP与OLAP最根本的区别。我们把政府信息系统中面向OLTP的数据库称为生产性(操作性)数据库,面向OLAP的数据库称为分析性数据库。......
2023-10-28

图5-1数据值诊断示例数据值诊断的顺序是首先选定诊断对象,收集元数据,利用收集的元数据分析数据文件、诊断数据值、分析文件结果、导出业务规则、进行品质测定,随后确认错误数据及进行原因分析后、整合质量诊断结果、提出改善方案等一连串的质量诊断流程。在数据值诊断中处于核心的数据文件分析与犯罪心理分析官(侧写员)从事的工作有很多相似的部分。......
2023-11-16

在数据库系统中,函数相当于数据库中的命令,可以通过调用函数来执行数据库中的相关功能;过程相当于数据库中能实现某个功能的一段程序。从右边取子串函数。Val+Val,其结果为33。删除字符串空格函数。Round,其结果为256.3。Int,其结果为123。?......
2023-12-04

图9-12 变量定义及地址分配2.参数组态按照前面介绍的步骤在程序中添加循环中断组织块OB202,在此OB中添加PID指令块,定义与指令块对应的工艺对象背景数据块。......
2023-06-15

,Ak,满足任何两个子集的交集非空,若再添加I的任何一个其他子集后将不再具有该性质,求k的值.解析:利用子集、补集的性质进行构造.例5集合A,B,C是I={1,2,3,4,5,6,7,8,9,0}的子集.若A∪B=I,求有序集合对(A,B)的个数;求I的非空真子集的个数.解析:利用子集、补集的概念解题.例6求1,2,3,…......
2023-08-13
相关推荐