计算机视觉测量技术以图像传感器为手段检测空间物体的空间三维坐标，进而检测物体的尺寸、形状和运动状态等。美国、加拿大、日本等发达国家早在20世纪60年代后期就已经开始了计算机视觉测量技术的研究。直到20世纪90年代，随着计算机技术的发展成熟，计算机视觉测量技术逐渐成为一个研究热点。......
2025-09-30
视觉测量技术：外极限约束与像点对应
【摘要】：显然，在观测到图像平面上一个像点时，由前面的讨论可知，与该像点相对应的物点必定满足下面的外极限约束条件。根据外极约束可知，为了在右图像上找到与PLi相对应的PRi，不必在整个右图像上进行探索，而只须沿相应的外极线进行探索即可。虽然上述外极约束提供了一个很有用的探索工具，可以帮助减少探索空间。但遗憾的是，外极约束本身并不保证一定能够惟一地在左、右图像平面上找到各自像点的对应点。
假定仅有关于物点的投影像的观测数据可以利用。显然，在观测到图像平面上一个像点时，由前面的讨论可知，与该像点相对应的物点必定满足下面的外极限约束条件。
左图像平面上的某个像点PiL在右图像上的对应点PRi必定在由左图像中过像点PLi的视线和右摄像机的光学中心O′所确定的平面π和右图像平面上的交线Le上。
为方便起见，称所述交线Le为外极线（Epi-polar Line），所述平面π为外极平面。根据外极约束可知，为了在右图像上找到与PLi相对应的PRi，不必在整个右图像上进行探索，而只须沿相应的外极线进行探索即可。这样做可以大大减少探索空间，从而大大缩短探索的时间。
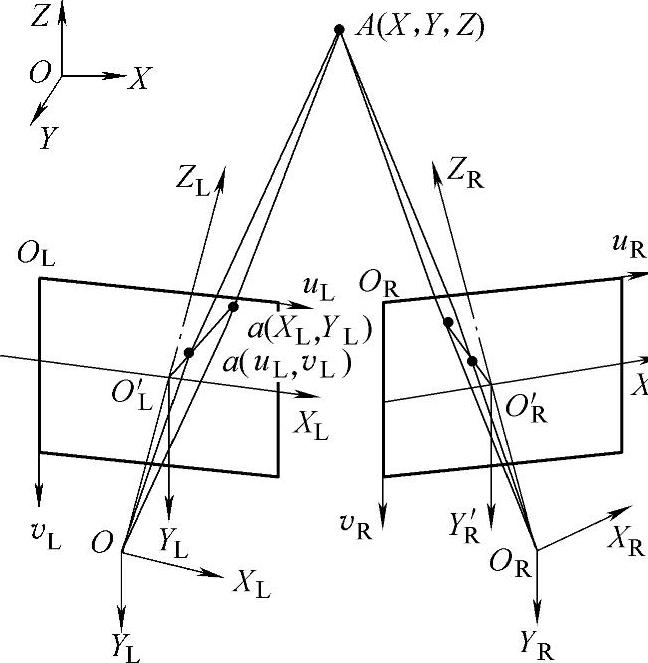
图7.18 双目测量原理
设定左摄像机O-xyz位于世界坐标系原点且无旋转，图像坐标系为
O＇L-XLYL，焦距为fL；右摄像机坐标系为OR-xRyRzR，图像坐标系为O＇R-XRYR，焦距为fR，双目测量原理如图7.18所示。根据摄像机透视变换模型有
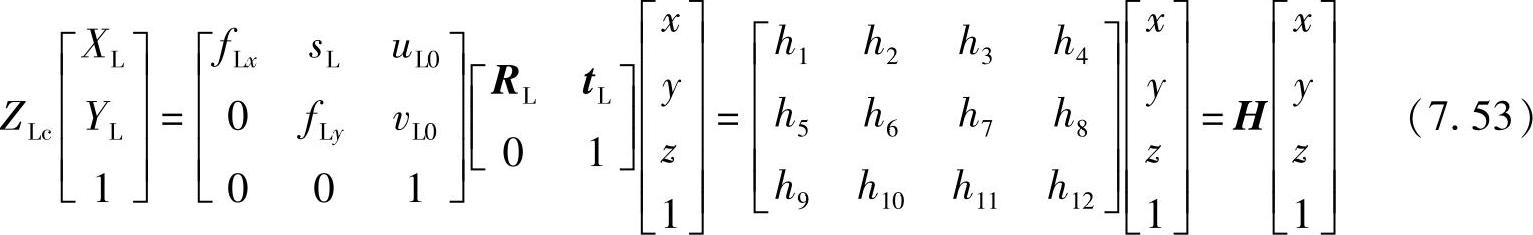
H为其投影矩阵，同理设右摄像机的投影矩阵为
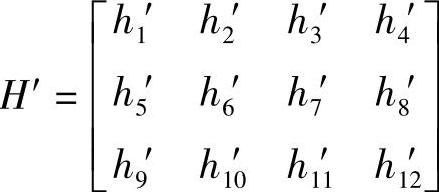
由两台摄像机的关系得到
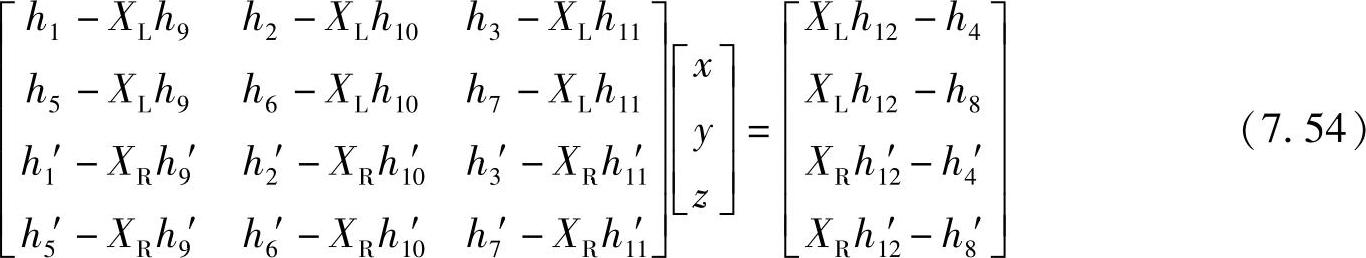
方程组中有3个未知数和4个方程。求该超定方程的最小二乘解即可得到（x，y，z）。(https://www.chuimin.cn)
当已知两台摄像机的内参数及空间点在左、右摄像机所拍摄图像中的图像坐标后，即可按照上述方法得到被测点的三维坐标。
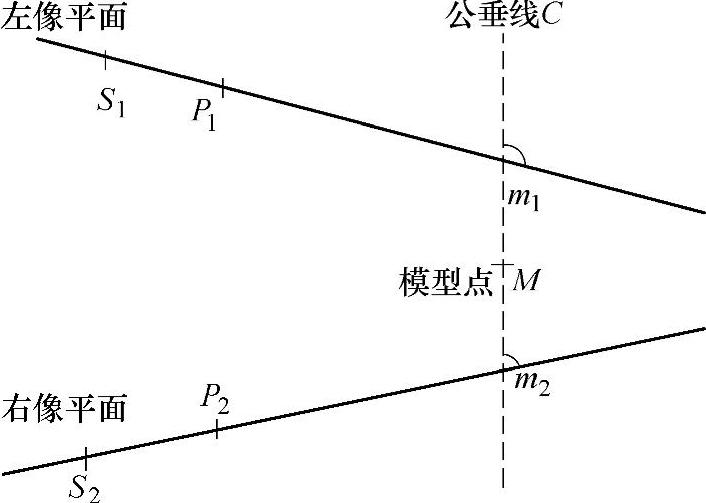
图7.19 公垂线原理
但是在实际应用中，摄像机的成像模型并非理想的小孔成像模型，而图像匹配点的确定和标定过程都会引入微小的误差，这使得图7.19所示的两条直线可能不会相交。由于这两条直线不可能平行，只能是异面直线。这两条直线无交点时，上述方程组无解，无法确定点A的空间坐标。为解决这种问题，可使用公垂线法计算空间点的坐标，相交直线可视为公垂线长度为零的特殊异面直线。
如图7.19所示，假设两条异面直线L1、L2方向矢量为l1、l2，点m1、m2分别为两条异面直线上的点。当‖m1m2‖值最小时，m1m2即为两条异面直线的公垂线。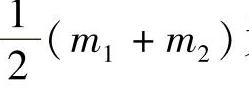
为公垂线中点的坐标。由异面直线的公垂线和异面直线的关系可以得到
即
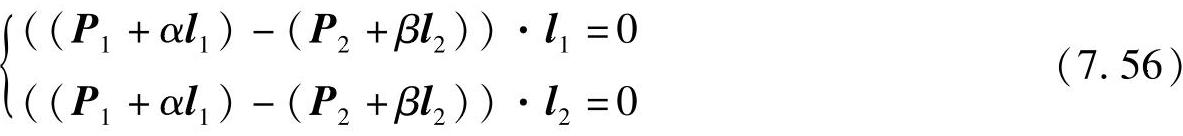
求解方程得到位置系数α、β为
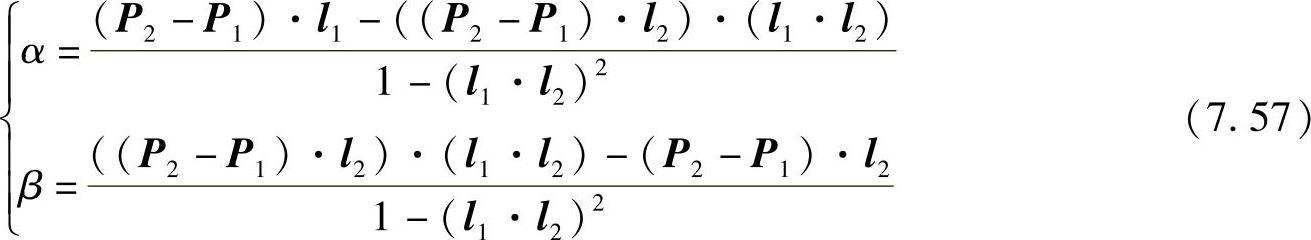
带入公垂线的直线方程中，求‖m1m2‖的大小。如果‖m1m2‖小于设定的阈值，则可认为空间点的坐标为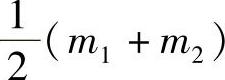
。
显而易见，立体视法成败的关键在于能否在左、右图像平面上找到各自的像点的对应点。虽然上述外极约束提供了一个很有用的探索工具，可以帮助减少探索空间。但遗憾的是，外极约束本身并不保证一定能够惟一地在左、右图像平面上找到各自像点的对应点。为了减少误对应，还需要引入其他约束条件。下面，对其中较重要的几个约束条件做一个简单介绍。
相关文章
- 详细阅读
-
Marr视觉理论简介：视觉测量技术详细阅读
下面简要介绍Marr视觉理论的基本思想和框架。图1.1 Marr视觉信息处理的三个阶段第一阶段是早期视觉处理，其目的是从输入的原始图像中抽取观察者周围景物表面的物理特性，如距离、表面方向、材料特性等，并构成要素图或基元图。表1.2 由图像恢复形状信息的表达框架3.Marr视觉理论的意义及不足Marr视觉理论是计算机视觉研究领域的划时代成就。图1.2 改进后的Marr视觉理论框架限于历史等因素，Marr没有研究如何用数学方法严格地描述视觉信息的问题。......
2025-09-30
-
双目视觉测量系统标定：视觉测量技术成果详细阅读
双目视觉测量系统的标定主要是指摄像机内部参数标定后，确定视觉系统结构参数R和T。实际上，在双目视觉测量系统的标定方法中，是由标定靶标对两台摄像机同时进行摄像机摄像标定，以分别获得两台摄像机的内、外参数，从而不仅可以标定出摄像机的内部参数，还可以同时标定出双目视觉测量系统的机构参数。......
2025-09-30
-
视觉测量技术：连通区域标记方案详细阅读
在扫描过程中，如果发现某个像素的灰度值由0变为1且没有分配标记，则给该像素分配一个没有使用的标记；如果当前正被扫描的像素值为1，则根据其与邻域像素的连通性对其进行标记；如果当前像素与多个目标相连通，则可以认为这些目标实际上是同一个，并把它们连接起来。......
2025-09-30
-
计算机视觉技术的应用领域：视觉测量技术详细阅读
在工业生产中，计算机视觉技术可以自动检测各种机械零件的几何尺寸，测量其精度范围，目前已经用于产品外形检验、表面缺陷检验等。2）利用计算机视觉技术进行病虫害的监测。在现代战争中，无人机发挥着举足轻重的作用。无人机导航是无人机技术的重要组成部分，基于计算机视觉的无人机导航技术是目前无人机导航领域的研究热点。......
2025-09-30
-
视觉测量技术-投影模式及优点详细阅读
图6.7 光条投影示意图利用该方法确定物点三维信息的优点是明显的。图6.9 灰度编码模式光投影法如图6.9所示，在投影仪光源的前方放置一个掩膜。......
2025-09-30
-
视觉测量技术的研究目标详细阅读
借鉴人类视觉的原理，计算机视觉技术研究的长远目标是建立通用的视觉系统。计算机视觉技术的优势不仅在于能模拟人眼的功能，还能完成人眼所不能胜任的工作。因此，对人脑视觉的充分理解将促进对计算机视觉更深入的研究，并对计算机视觉系统提供坚实的生物理论基础。......
2025-09-30
-
实现精确测量的视觉技术详细阅读
具体来说，计算机视觉测量系统的关键技术主要包括光源照明技术、图像处理与分析技术、摄像机标定技术、三维测量技术、图像拼接技术和三维重构技术等。而图像处理器的发展也为工业图像测量系统带来了新的机会和技术问题解决方案。......
2025-09-30
相关推荐