首页理论教育视觉测量技术：系统结构参数对测量精度的影响分析

视觉测量技术：系统结构参数对测量精度的影响分析

2023-11-24 理论教育版权反馈

【摘要】：式有时还写为以为观测值的正直摄影精度估算当以为观测值时，式可写为不考虑摄影基线误差mB和主距误差mf，而以为误差源，式的微分式为或写为转为中误差形式，并认定mx1=mx2=my1=m，则有式和式是近景摄影测量中，以正直摄影方式进行摄影时，对精度预先实施粗略估算的常用式。7）两台摄像机的有效焦距越大，视觉测量系统的测量精度越高，即采用长焦距镜头容易获得较高的测量精度。

1.两台摄像机光轴平行的精度估算

如图7.6所示，对于两台摄像机光轴平行，取摄影坐标系S₁-XYZ，其原点为左摄影中心S₁，Z轴与左主光轴重合。X轴为基线B的方向。设图像坐标系

O_l-x₁y₁及0₂-x₂y₂，均与S_1-XY平行。某目标点A在S₁-XYZ内的坐标为（X，Y，Z），或写作（X，Y，-H），则存在以下关系：

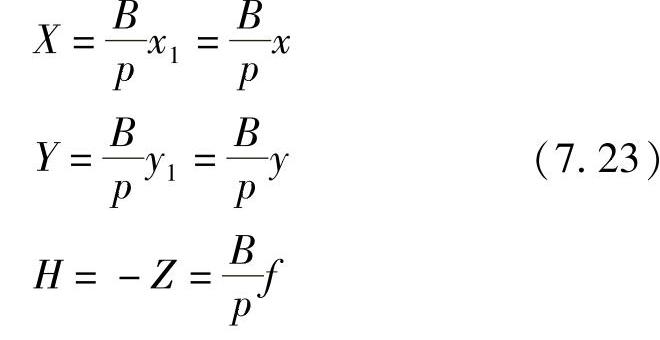
或写为

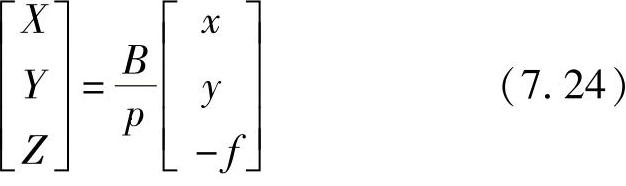
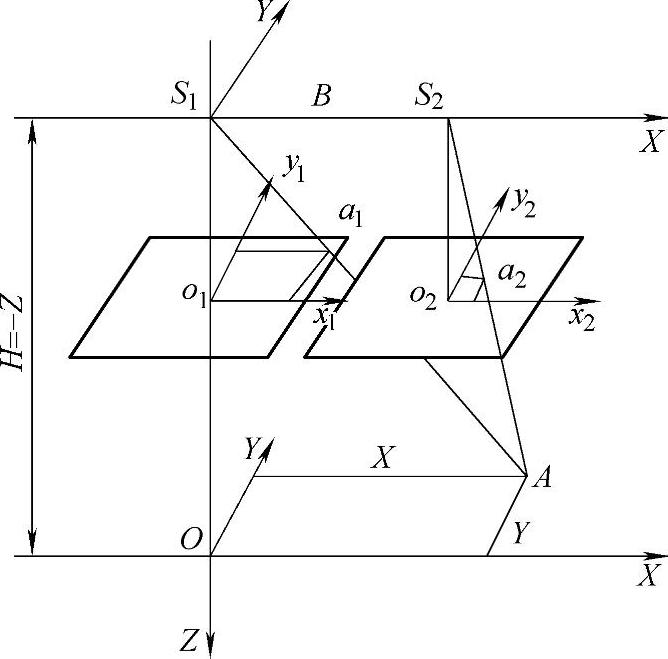
图7.6 两台摄像机光轴平行摄影方式

（1）以（x，y，p）为观测值的正直摄影精度估算

如不考虑摄影基线误差m_B和主距误差m_f，而仅以（x₁，y₁，p）为误差源，式（7.23）的微分式为

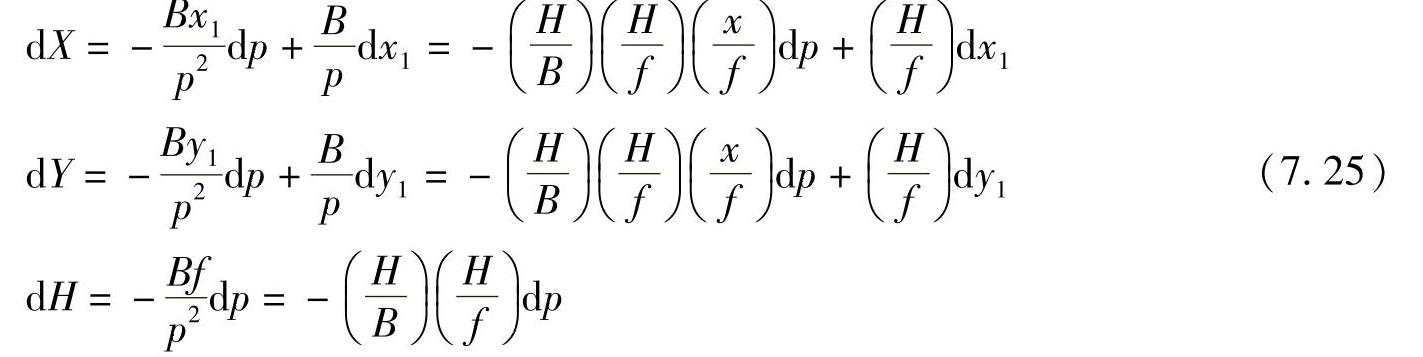
式中，（X，Y，Z）为目标点物方坐标；B为摄影基线；p为像点左右视差p=（x₁-x₂）；（x，y）为像点坐标，这里以x代表x₁，以y代表y₁；f为所处理图像主距。这时目标点物方空间坐标可表示为

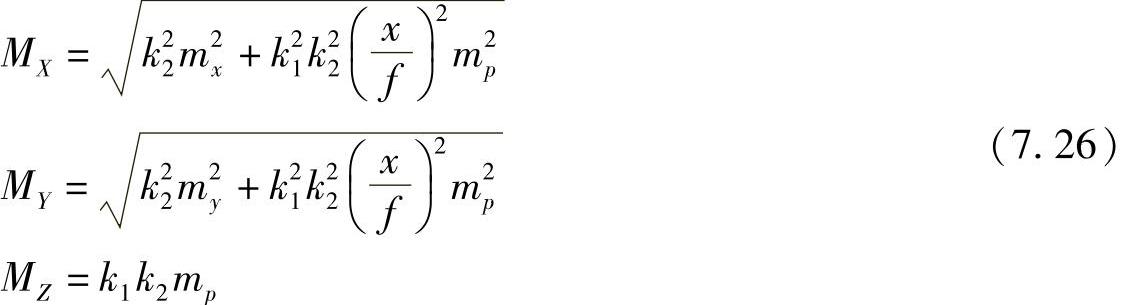
式中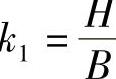，，称为构形系数，它与目标点同名光线间的夹角有关，即摄影基线越大、目标点越近，k₁值越小、目标点测定误差越小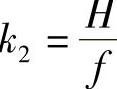；，称为成像比例尺分母系数，即所处理的图像主距越大、目标点越近，k₂值越小、目标点测定误差越小。式（7.26）有时还写为

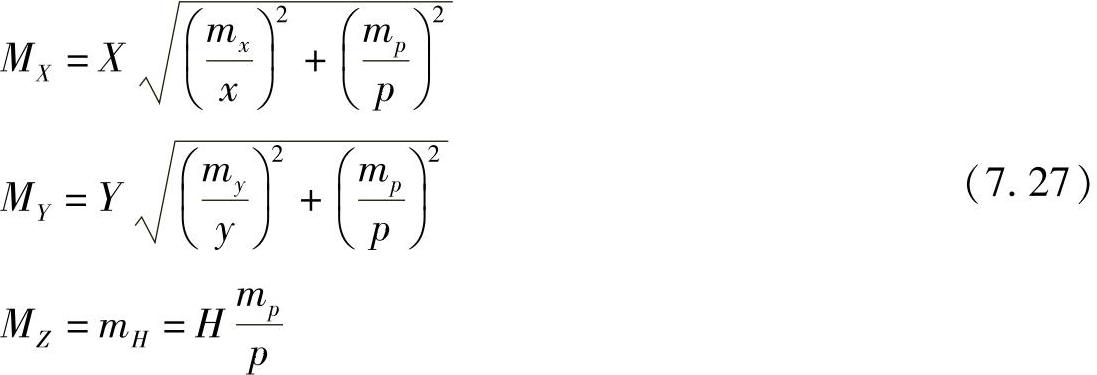
（2）以（x₁，y₁，x₂，y₂）为观测值的正直摄影精度估算

当以（x₁，y₁，x₂，y₂）为观测值时，式（7.24）可写为

不考虑摄影基线误差m_B和主距误差m_f，而以（x₁，x₂，y₁）为误差源，式（7.28）的微分

式为

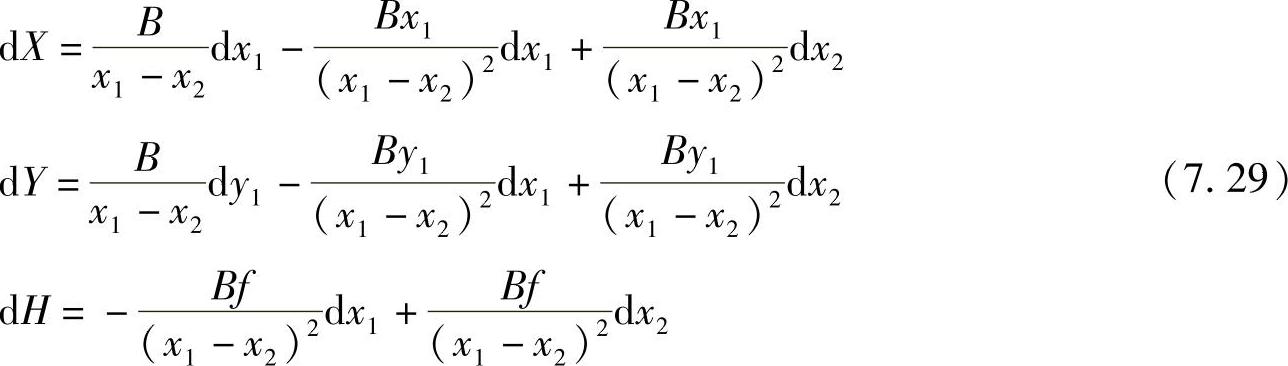
或写为

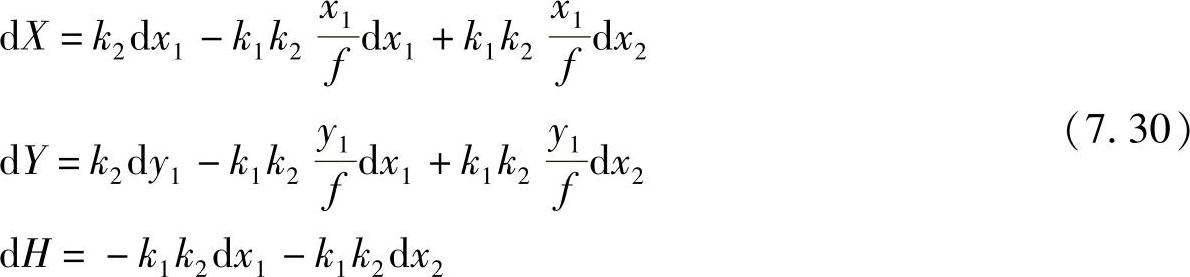
转为中误差形式，并认定m_x1=m_x2=m_y1=m，则有

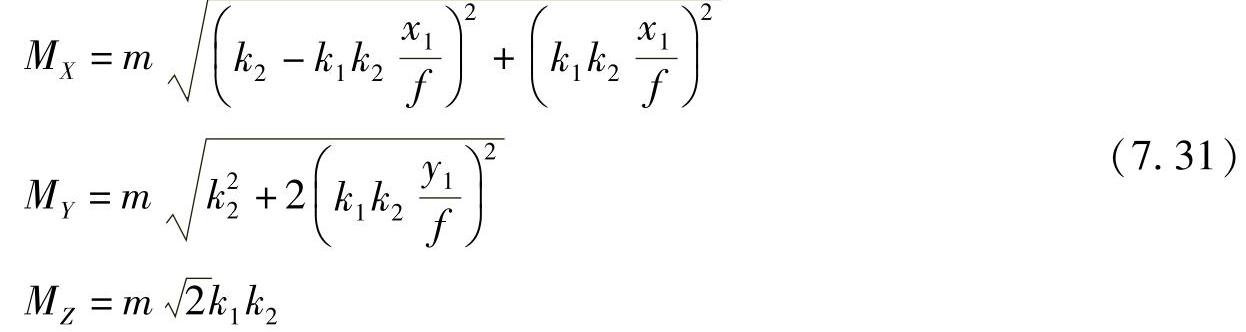
式（7.26）和式（7.30）是近景摄影测量中，以正直摄影方式进行摄影时，对精度预先实施粗略估算的常用式。分析它们可得如下结论：

1）为了提高精度，应尽可能减小成像比例尺分母系数k₂，尽量拍摄大比例尺图像，即尽可能缩短摄影距离Z。

2）为了提高精度，应使摄影基线B尽量大，即减小构形系数k₁。

3）为了提高物方点测定精度（M_X，M_Y，M_Z），应提高像点位置的质量，包括提高量测精度和去除影响像点位置的各类误差。即这些式中的（m_x，m_y，m_z）应理解为是形容位置质量的一种综合性指标，而不仅仅是测量误差。

4）一般情况下，远近方向的测定中误差M_Z最大，所以常以M_Z=k₁k₂m_p来估算摄影测量的精度。

5）若需考虑基线B的误差和等效焦距f的误差，应参照更为详细的精度估算式。若不能维持标准的正直摄影，则还应考虑外方位角元素和外方位直线元素误差的影响，还应参照更为详细的精度估算式。

6）有些情况下，式（7.26）可粗略简化为

式（7.32）可粗略简化为

不难看出，对正直摄影方式而言，一般有m_z＞m_x或m_z＞m_y。

7）两台摄像机的有效焦距越大，视觉测量系统的测量精度越高，即采用长焦距镜头容易获得较高的测量精度。

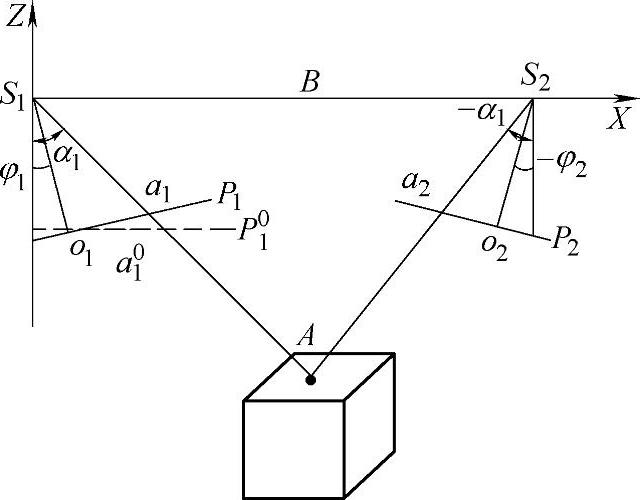
图7.7 交相摄影方法

2.两台摄像机光轴汇聚方式的精度估算

假设自摄站S₁与S₂拍摄了有一交向摄影图像对（P₁，P₂），如图7.7所示。两图像（P₁、P₂）仅有偏角，分别为φ₁与φ₂。为了讨论交向摄影的精度，设有虚拟的无倾角图像对（P⁰₁，P⁰₂），图中未表示P⁰₂。

有φ角的情况下，“水平”图像上点a⁰₁与“倾斜”图像上点a₁的坐标关系式为

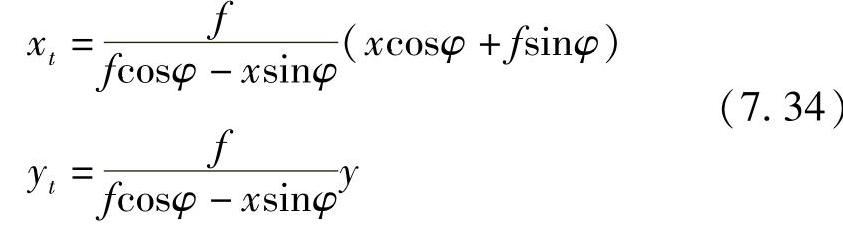
或写为(www.chuimin.cn)

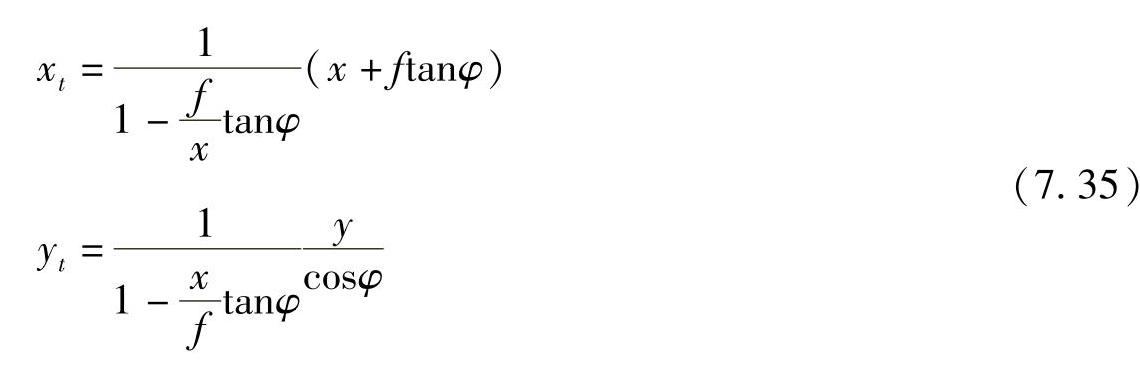
为了确知“倾斜”图像上点位坐标误差对“水平”图像上点位误差的影响，现对（x，y）取微分，有

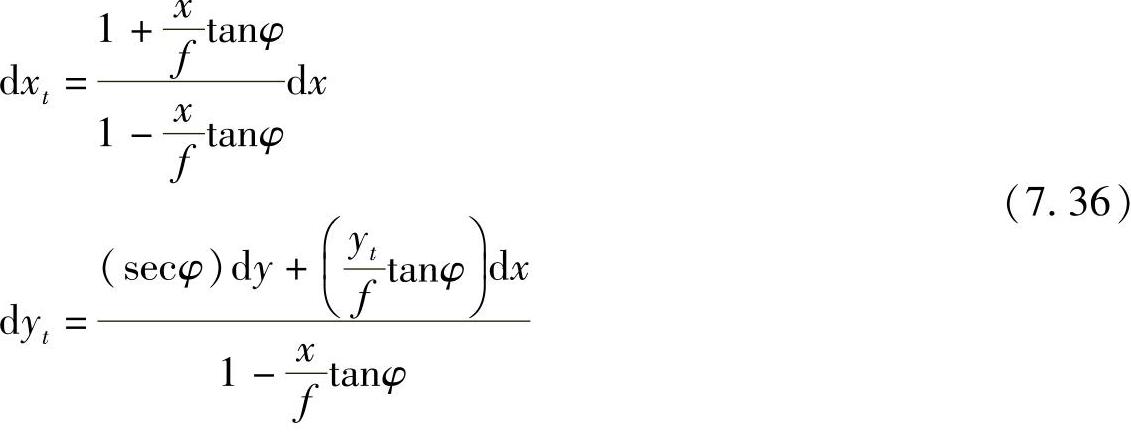
推演式（7.36）时应用了可以从式（7.35）直接写出的如下两个关系式：

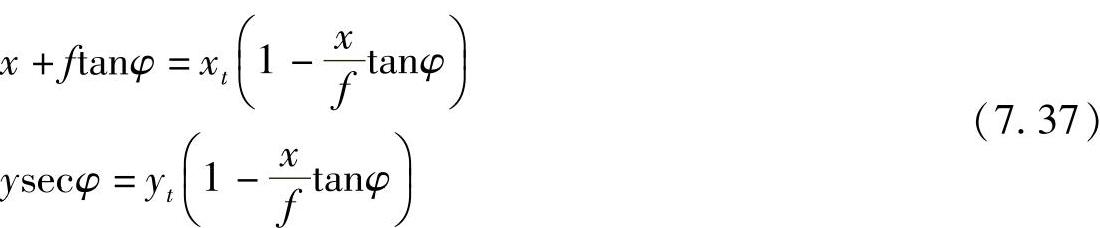
将式（7.36）转为中误差形式，“水平”图像点位中误差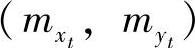与“倾斜”图像点位中误差（m_x，m_y）的关系式为

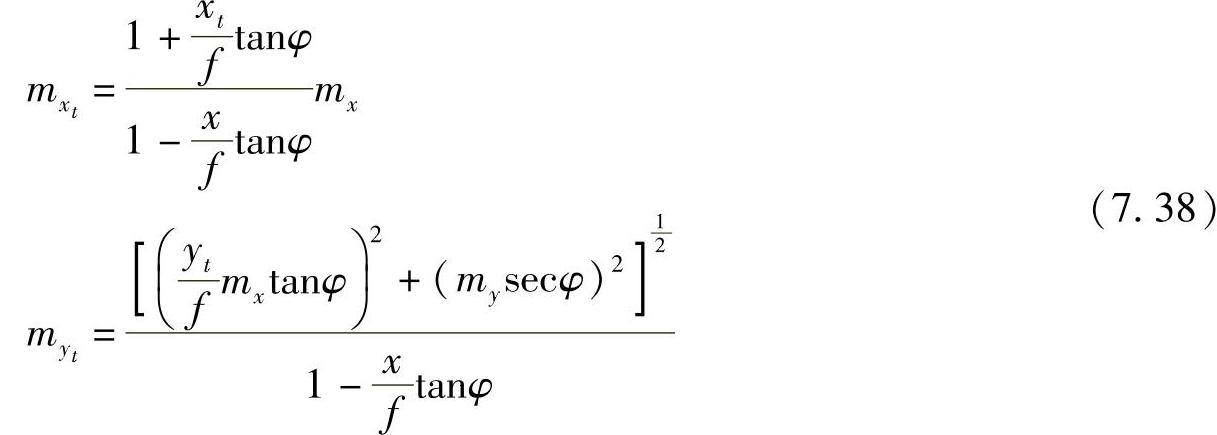
根据图7.7，又有如下两个关系式：

故式（7.38）可改写为

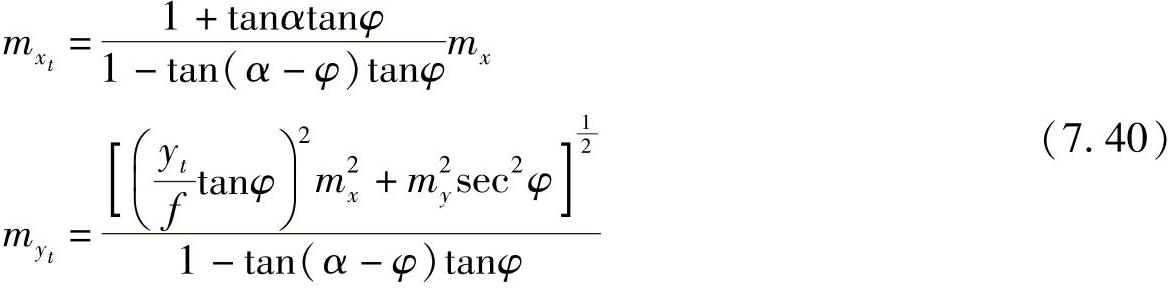
现又假设点A位于平面XZ内，即认为y_t=0，因而式（7.40）可简化为

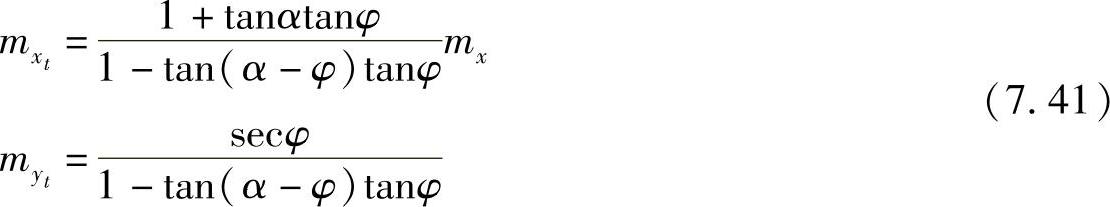
式中，（m_x，m_y）为“倾斜”图像上的坐标测量中误差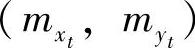；实际上是式（7.30）中的（m_x，m_y）。因而，在交向摄影方式情况下，物方点的坐标中误差式为

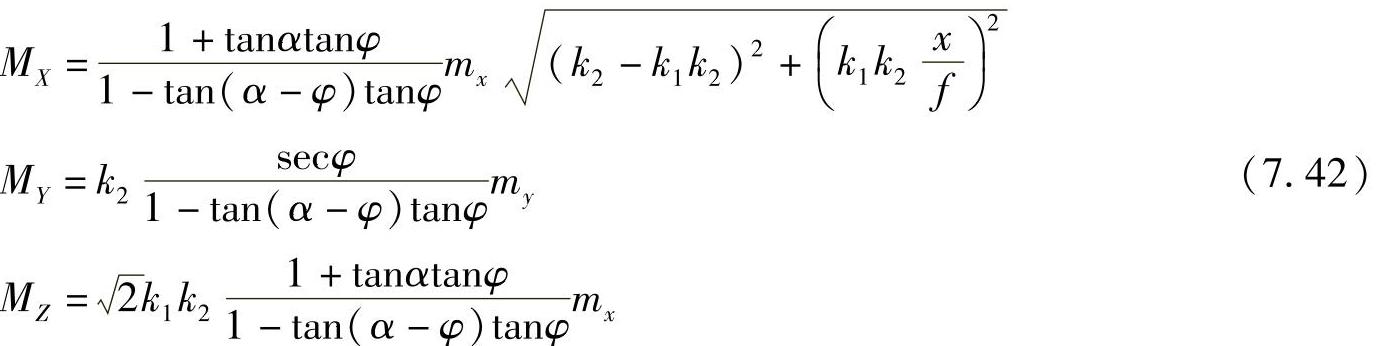
现在，假设仅讨论两主光轴焦点O的精度，如图7.8所示。且已知

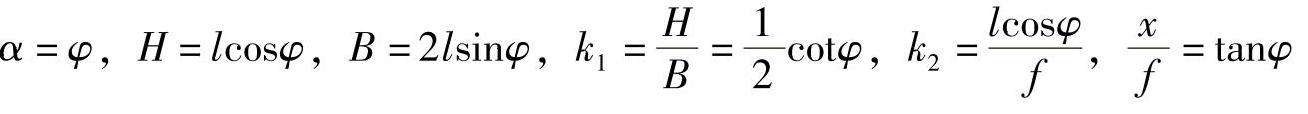
另外，O点处成像比例分母系数未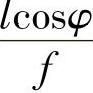。故式(7.42)应写为

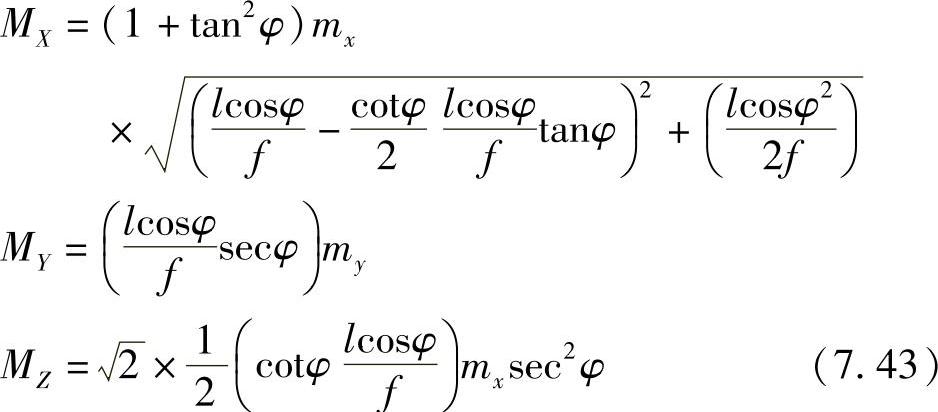
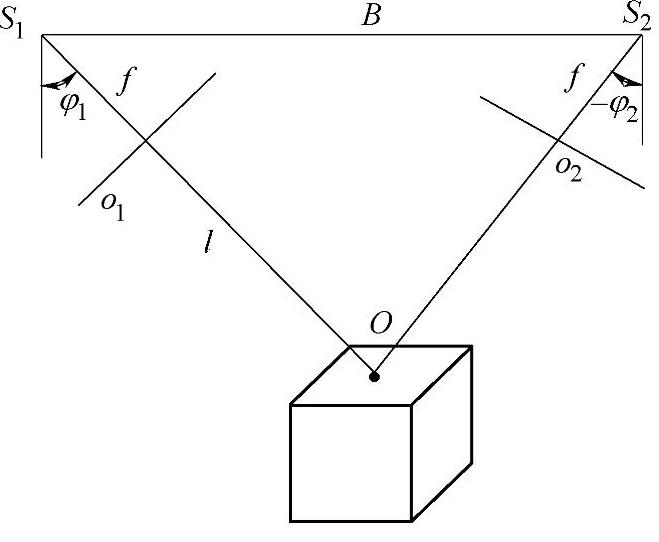
图7.8 交相摄影方式精度估计

化简后的两台摄像机光轴汇聚方式精度估算式为

如上所述，式(7.44)是在单像对称交向摄影的条件下，讨论两主光轴交点处O的精度估算式。注意到，M_Y与图像倾斜角φ的大小无关。

现在研究在怎样的交向角情况下，可使总误差为最小，即使

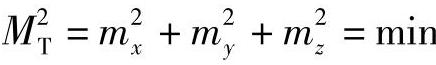
换言之，令

m_x=m_y=m，有

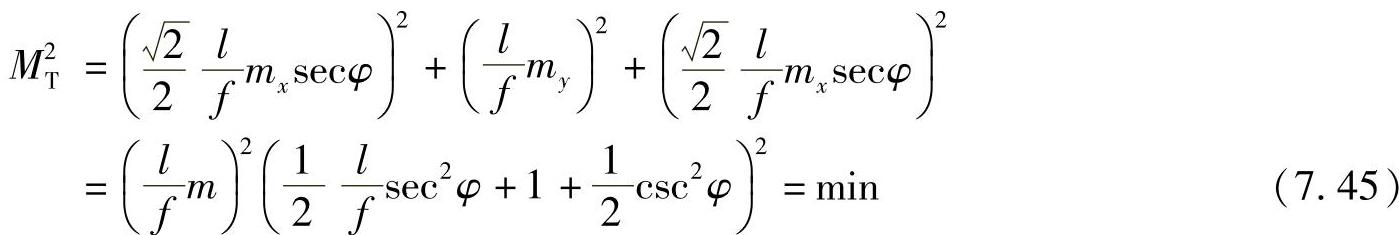
取式(7.45)的有效部分

对φ取导数，并令之为零

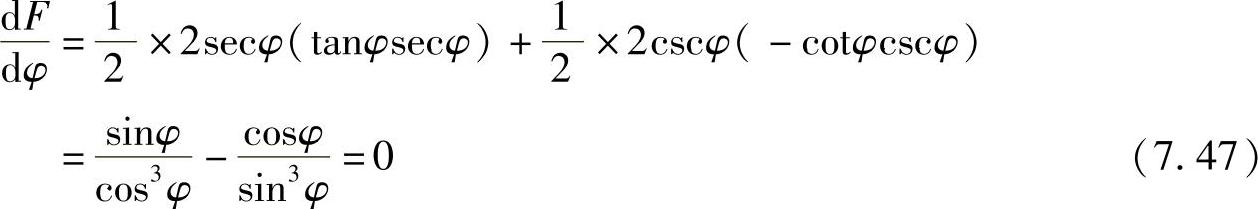
即有

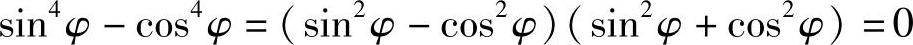
或写为

由式（7.48)可知，为使总误差M_r最小，应使图像倾斜角φ=45°，交向角为90°。此时，摄影距离为l，基线B与“航高”皆为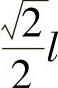。并且，当以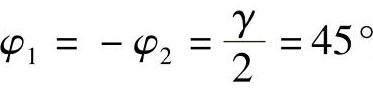进行摄影时，物方点O的精度按式（7.43）为

即在（X，Y，Z）三个方向得到相同的精度。

经过对上述对交向摄影方式精度的讨论，得到如下结论：

1）当交向角为90°时，总误差最小，且各方向中误差相等。

2）为提高交向精度，应增大摄影比例尺，提高像点坐标量测精度，注意交会角度对各方向坐标精度的影响。