首页理论教育Subbarao深度恢复算法：视觉测量技术快速准确

Subbarao深度恢复算法：视觉测量技术快速准确

2025-09-30 理论教育版权反馈

【摘要】：由于所处理的是图像子块，所以认为是同一距离的，因此σ近似为恒定的。解出σ2后，代入式即可得到物体的景深，即2.微幅改变摄像机参数获取景深Subbarao提出的第二种方法是微幅改变摄像机的参数，假设其中一幅图像的参数是v01、f1、r，则另一幅图像的参数是v01+ds、f1+df、r+dr。

Pentland提出的第二种散焦测距方法中，一幅图像是通过设置正常光圈获取的，另一幅图片必须在针孔模式下获取的，即将光圈调到非常小时获取另一幅图像。这种方法在实际应用上存在一些问题，例如光圈太小容易形成衍射效应，从而使图形失真。而且小光圈的进光量太少，要增加曝光时间。这就使Pentland的方法在应用上受到限制。

1.通过调节摄像机镜头孔径的深度恢复算法

针对Pentland方法的不足，2025年Subbarao放宽了Pentland方法中必须将其中一张图像的摄像机镜头孔径调到最小限制。通过调节镜头的孔径，在相同的像距下，对相同的景物取两幅图像。由于镜头孔径的不同，因此得到的两幅图像的模糊程度也不同。成像几何模型如图6.23所示，由几何光学透镜成像公式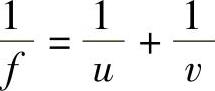，根据相似三角形关系，可以得到

因此可以得到

将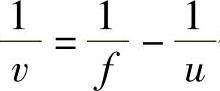代入式（6.72）得

因此，当物距的保持不变时，随着v₀的大小变化，d可正可负。将式（6.73）代入式（6.52）可以得到

点扩散函数定义为二维高斯函数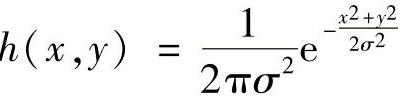；扩散参数σ=kd，h（x，y）的傅里叶变换为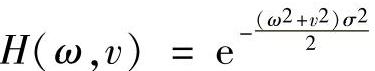；ω、v是空间频率；模糊参数σ在不同距离时是不等的。由于所处理的是图像子块，所以认为是同一距离的，因此σ近似为恒定的。

一个图像块的模糊参数σ可以通过一个或多个参数来改变，保持物体到摄像机镜头的距离不变，随意改变其他变量的数值获取两幅图像。P₁（ω，v）和P₂（ω，v）为这两幅图像对应的功率谱密度，其摄像机参数分别为v₁、f₁、D₁和v₂、f₂、D₂，σ₁和σ₂为其对应的模糊参数。

根据图像功率谱密度的定义，即

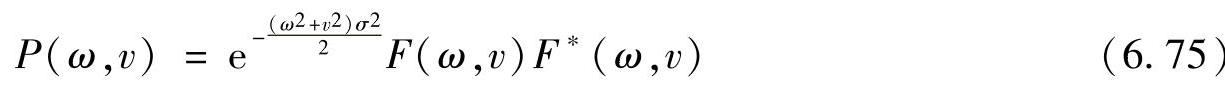
可以得到不同镜头孔径下的两个图像的功率谱密度表达式，即

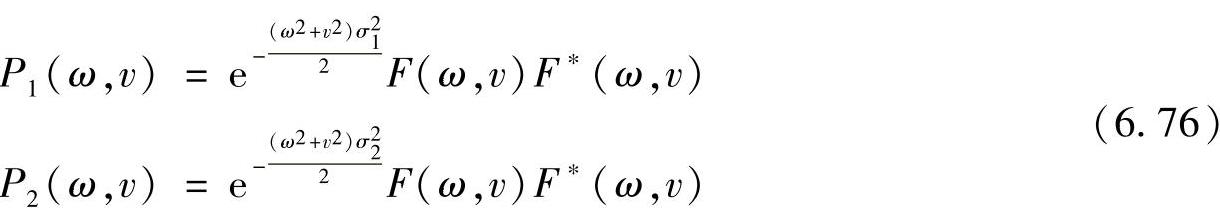
式中，F（ω，v）为理想图像I₀（ω，v）的傅里叶变换；F（ω，v）为其傅里叶变换的共轭。根据式（6.76）可以得到

对式（6.77）两边取对数并进行相应的整理，可以得到

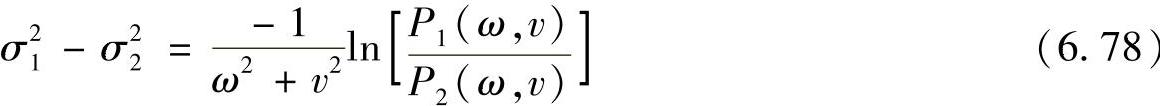
对于某一个给定的（ω，v），式（6.78）的右边可以由给定的图像对计算出，所以可以用式（6.78）来估计σ²₁-σ²₂的值。理论上，测量一点（ω，v）的功率谱密度就能得到σ²₁-σ²₂的一个估计值。为了获得更好的鲁棒性，在一个频域空间内取平均值，即

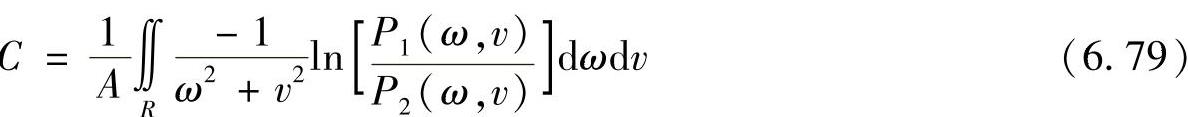
式中，R是（ω，v）空间里不包括G₁（ω，v）=G₂（ω，v）成立的（ω，v）的集合区域；A是R的面积；C是σ²₁-σ²₂平均值。因此有

式（6.80）中有两个未知数，可以由实际的摄像机参数设置来获得如下方程而求得：

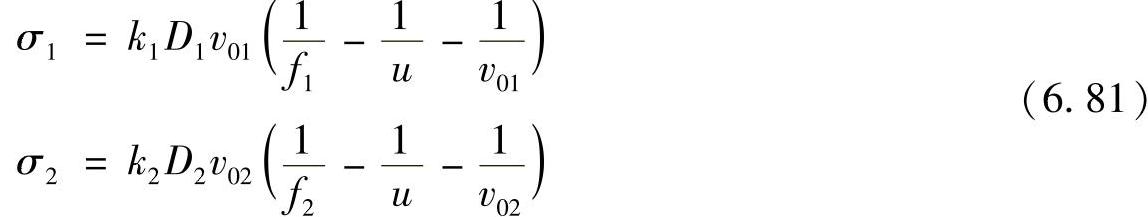
消去（6.81）中的变量u，即可得到

其中

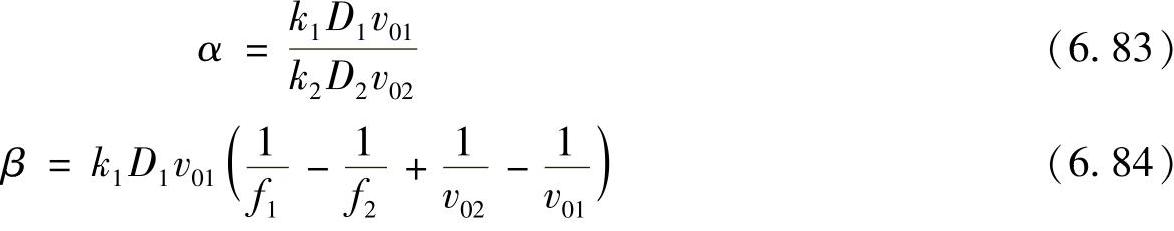
联立式（6.81）和式（6.83），消除变量σ₁可以得到关于σ₂的表达式，即(https://www.chuimin.cn)

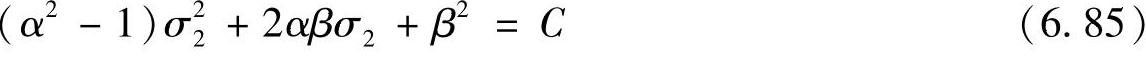
这是一个关于σ₂的一元二次方程，通常情况下它有两个解，而当u₁=u₂时有惟一解。解出σ₂后，代入式（6.81）即可得到物体的景深，即

2.微幅改变摄像机参数获取景深

Subbarao提出的第二种方法是微幅改变摄像机的参数，假设其中一幅图像的参数是v₀₁、f₁、r，则另一幅图像的参数是v₀₁+ds、f₁+df、r+dr。对图像功率谱密度函数进行求导可得

因此

令

理论上只要测量出一点的P和dP的值就可以求出C。为了获得更好的鲁棒性，一般取一个区域的平均值，即令

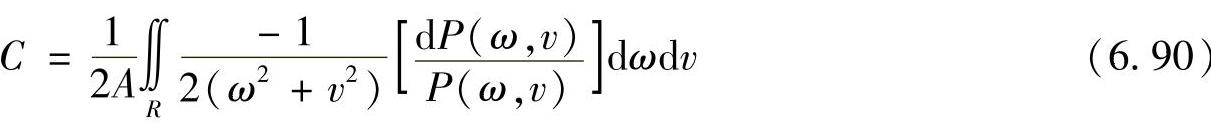
式中，R为不包括dP（ω，v）=0的频率区域；A是R的面积。根据式（6.88）对σ求导可以得到

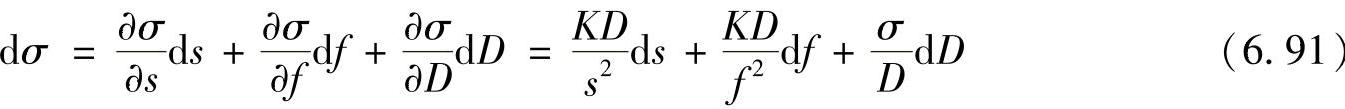
由式（6.91）代入式（6.88）可以得到

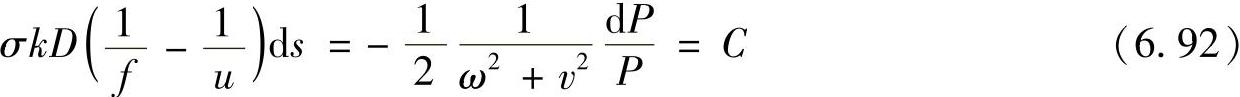
把式（6.74）带入式（6.92）可以得到

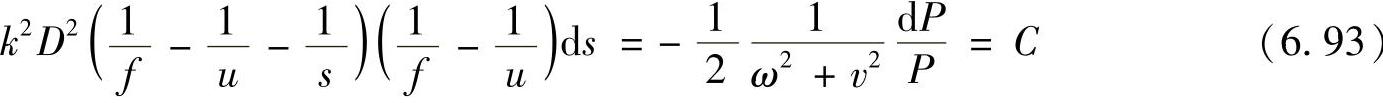
为了表示方便，设

因此式（6.93）可以表示为

对式（6.96）进行未知参数X的求解，得到

因为在正常的实验条件下f＜u＜∞，所以有

将式（6.98）代入式（6.95），并进行适当整理可以得到物体的距离u，即

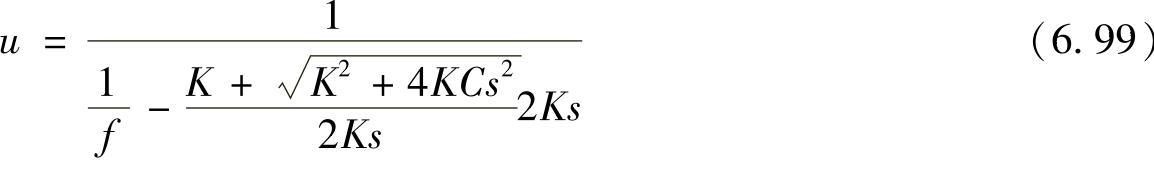
物体的距离也可求。