先利用线性变换方法或透视变换方法求解摄像机参数，再以求得的参数作为初始值，考虑畸变因素，利用非线性优化方法进一步提高标定精度，就形成了所谓的两步法。两步法计算量适中、精度较高。摄像机坐标系定义为原点在摄像机光学中心，z轴与光轴重合。......
2023-11-24
摄像机标定-双平面法
【摘要】：利用这些转换系数，图像平面上的任意一点P，都可以在两个参考平面上找到点P1、P2与之对应。通过式连接P1、P2，可得到点P的视线，有了视线方向，便可以很容易地进行立体三角测量。
双平面法中没有明确的使用摄像机的模型，它是通过两个已知相关平面上的点到图像坐标上对应点的连线，利用插入的方法求得摄像机的相关参数。
假设在空间中有两个参考平面：π1，π2。在这两个平面上，分别定义坐标系O1-X1Y1Z1和O2-X2Y2Z2。其中，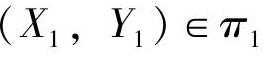
，
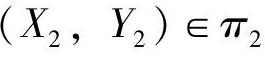。这两个参考系统的相互转换关系可以用旋转矩阵R和平移矢量T来表示，即
式中，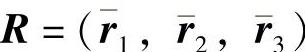
，
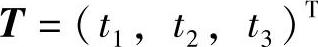。因此，对于平面π2上任何一点P2：（X2，Y2）∈π2，都可以在π1中表示为
假设在两个平面上有许多这样相关的点，那么这些点与它们相对应的图像上的点之间的转换可以通过二维透视变换法来描述。对于平面π1，相关的变换可以写为
摄像机像坐标（x，y）可以用像素坐标系来表示，即
和
。将之带入式（5.202），并用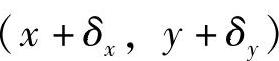
代替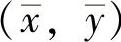
。其中，（x，y）为经过镜头畸变后的真实图像坐标，（δx，δy）为修正畸变而做的补偿。最终得到的一般表达式如下：(www.chuimin.cn)
同样，平面π2和图像平面上的点也可以写为
式（5.203）～式（5.206）构成了一组利用系数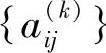
和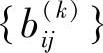
计算的等式，通过这些等式可以直接用线性的方法来计算出摄像机内在和外在的参数。利用这些转换系数，图像平面上的任意一点P，都可以在两个参考平面上找到点P1、P2与之对应。通过式（5.201）连接P1、P2，可得到点P的视线，有了视线方向，便可以很容易地进行立体三角测量。
这种双平面的标定模型是由Martins等人首先提出，但他们的计算方法只有在参考平面平行于图像平面时才有效。这种方法的优点是只利用线性方法就可以解得有关参数，缺点是要求解大量的未知参数；存在过分参数化的倾向。
有关视觉测量技术的文章
- 详细阅读
-
摄像机标定的透视变换法详细阅读
不考虑摄像机镜头的非线性畸变，那么从物体点的三维到图像点的二维变换是线性变换，透视变换中的系数为未知数。以上介绍了摄像机标定的透视变换法的计算过程，在用真实数据进行实验时，需要注意以下问题：1）矩阵M确定了空间点坐标与它的图像点坐标的关系。......
2023-11-24
-
快速标定CCD摄像机的技巧详细阅读
周富强 邾继贵 杨学友 叶声华摘要：在视觉检测系统中，针对视觉传感器数量多，且每个摄像机需标定的内部参数及外部参数较多的特点，提出了一种新的简单的快速摄像机标定方法。分析了摄像机的各个关键参数，采用了全线性标定方法和矢量分析法，逐步求出CCD摄像机的参数。实际结果表明，摄像机标定误差优于0.05mm。......
2023-06-23
-
视觉测量技术-张正友法的摄像机标定成果详细阅读
张正友法是介于传统标定方法和自标定方法之间的一种方法。张正友法采用平面标定模板，只需对标定模板的不同方向进行拍摄，而不需知道标定板的运动方式。图5.20 张正友法标定流程1.基本投影方程符号说明首先，根据前述的摄像机模型，对本小节中将要用到的符号进行说明。它们的齐次矢量表示形式分别为，。在这种情况下，需要用非线性优化使这种偏差达到最小，从而获得使偏差最小时的参数为摄像机参数的估计值。......
2023-11-24
-
摄像机标定的原理、方法及结果详细阅读
其中，直接线性变换是最优化算法，两步法进一步考虑了畸变补偿，双平面法合理运用了摄像机的成像模型。3）将各标定点相应的像平面坐标（u，v）及世界空间坐标代入摄像机模型式中，根据标定方法，求解摄像机内外参数。......
2023-11-24
-
摄像机标定过程中的两步法详细阅读
图5.17 直接光学法确定图像中心的标定原理4）基于中心无畸变区的摄像机光学中心标定方法 基于中心无畸变区的摄像机光学中心标定方法利用的是透视成像的基本原理。求解光学中心的矩阵表达式对式和式用最小二乘法求解，便可得到模板点的轨迹方程和光学中心坐标。给定r1、r2、r4、r5，则R有两个解，另一个为具体选择哪一个，可由试探法确定。......
2023-11-24
-
视觉测量技术：摄像机标定方法及系统详细阅读
多数情况下，这些参数必须通过实验与计算才能得到，这个过程称为摄像机的标定。摄像机标定一般分为经典标定方法和自标定方法。当前对传统摄像机标定技术的研究集中在非线性畸变校正。自标定方法不依赖于标定参照物，仅利用摄像机在运动过程中周围环境的图像与图像之间的对应关系对摄像机进行标定。图5.1 摄像机标定系统图5.2 标定靶标的控制点类型......
2023-11-24
-
平面辅助投影：换面法详细阅读
图3-49将一般位置平面变为投影面垂直面例3-22求△ABC对H面的倾角α。图3-52将一般位置平面变为投影面平行面作图作图方法如图3-52所示，先换H面，得到投影面垂直面的投影及β角，然后换V面得到△ABC的实形。......
2023-06-28
相关推荐