不考虑摄像机镜头的非线性畸变,那么从物体点的三维到图像点的二维变换是线性变换,透视变换中的系数为未知数。以上介绍了摄像机标定的透视变换法的计算过程,在用真实数据进行实验时,需要注意以下问题:1)矩阵M确定了空间点坐标与它的图像点坐标的关系。......
2025-09-30
1.内部参数预标定
(1)图像中心标定
图像中心(u0,v0),即光轴穿过图像平面之点,理论上是像平面的中心点,但在应用中图像实际中心与理想像平面中心并不重合。产生这种现象的原因是多方面的,如摄像机CCD安装平面与光轴存在倾角误差;图像采集卡的窗口电路未将其窗口取在正中间,使光心偏离;图像采集卡采样的时序错误,造成每一行采样的开始时间不同。
1)变焦距法 在摄像机透镜系统中,当透镜有效焦距变化时,图像区域发生变动,但图像区域中心将稳而不变。若在有效焦距变动时,设所取针孔沿光轴方向移动,显然此时图像区域中心将处于光轴与图像的焦点上。此点即是成像中心。即用改变有效焦距的方法可以确定镜头的光学中心。用变焦距法标定镜头光学中心时,其标定精度是最低的,标定误差可达28像素,重复性为±20像素,故此方法一般只用于透镜光学中心的粗略估计。
2)径向准直约束法 径向准直条件是指当成像中心确定无误差时,根据空间坐标变换和成像关系,可将径向约束条件方程进一步表示为

采用平面模板,设置世界坐标系时使Z=0,则式(5.135)变为

取5个以上的标定点,则可通过非线性求解部分参数,然后通过非线性迭代方法求解径向畸变系数、有效焦距、平移矩阵T及畸变中心。可以通过寻找使式(5.136)残差最小的点坐标值来找到光学中心。
3)直接光学法 标定原理如图5.17所示。当激光束射向镜头表面,大部分光束透过镜头,部分光束由镜头各表面反射。当激光束与镜头光轴不同轴时,在激光束出射光阑面上可观察到由反射光束形成的多个亮度不同的、分布在光阑面上不同位置的干涉光斑。此时调整激光束相对于镜头的位置,到所有的反射干涉光斑均与激光出射光束重合时,表明此时激光束与镜头轴线同轴。此时打开摄像机,激光束在CCD像面上的像点即为镜头光学成像中心。需指出的是,必须仔细观察、耐心调整、尽可能将所有干涉光斑,包括某些不易察觉的非常暗淡的光斑,都要调整到与激光出射光束重合。否则,对镜头光学中心的标定偏差值及其重复性有很大影响。直接光学法原理简明,可用于对镜头成像中心直接进行标定,而与其他标定参数无关。实验表明,该方法标定精度高,重复性好,是一种可行的标定镜头光学中心的方法,标定结果在实际系统中效果良好。

图5.17 直接光学法确定图像中心的标定原理
4)基于中心无畸变区的摄像机光学中心标定方法 基于中心无畸变区的摄像机光学中心标定方法利用的是透视成像的基本原理。即一组与光轴平行的平行线在无限远处的交点,在图像平面上对应成像点是光学中心,也是消隐点。光学中心标定方法原理如图5.18所示,图5.19所示是光学中心标定模板,提取黑色方格的4个亚像素角点。在图5.18中点A1、A2、A3,B1、B2、B3,C1、C2、C3,D1、D2、D3分别是模板点A,B,C,D三次成像对应点,对应坐标(xmi,ymi)。其中,m=A,B,C,D;i=1,2,3。它们分别拟合出4个模板点A,B,C,D在平直导轨上移动轨迹(4条平行线)所对应的直线轨迹方程ymi=kxmi+bm,其矩阵求解形式为

通过对这4条直线方程进行拟合求解交点,可以得到光学中心(u0,v0)。求解光学中心的矩阵表达式

对式(5.137)和式(5.138)用最小二乘法求解,便可得到模板点的轨迹方程和光学中心坐标。

图5.18 光学中心标定方法原理

图5.19 光学中心标定模板
(2)尺度因子标定
对尺度因子μ进行标定时可以垂直拍摄一个圆环,然后计算其图像水平方向和垂直方向的直径像素比,即为所求尺度因子μ。这种方法简便且能够保证精度。
2.标定过程
当使用两步法进行单平面模板标定时,尺度因子需要事先标定。当标定点共面时可选取世界坐标系,使Z=0。这时式(5.134)中,r3/Ty、r6/Ty两项系数恒为零,于是有(https://www.chuimin.cn)

第一步:求解旋转矩阵R和T中的Tx、Ty。
1)拍摄一幅具有若干共面特征点的标定模板图像,利用图像处理方法确定若干个特征点的图像坐标,设共N个点,图像坐标为(xi,yi),i=1,…,N。并且,假设这些点相应的世界坐标为(Xi,Yi,Zi)。
2)对每个点按1)可列出一个方程,联立这N个方程,利用最小二乘法解这个超定方程组(N≥5),可解得如下变量:

3)利用R的正交性可以算出Ty和r1~r9,具体步骤如下:首先,计算Ty,有

式中,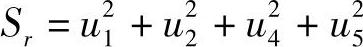 。其次,在求得Ty后,还要确定Ty的符号。由成像几何可知,x和X应有相同的符号,y和Y也有相同符号,可以利用这一点来确定Ty的符号。即在求得Ty后任选一特征点Pk,先假定Ty为正,有
。其次,在求得Ty后,还要确定Ty的符号。由成像几何可知,x和X应有相同的符号,y和Y也有相同符号,可以利用这一点来确定Ty的符号。即在求得Ty后任选一特征点Pk,先假定Ty为正,有
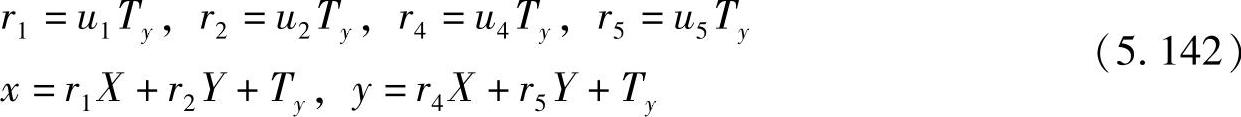
若x与x,y与y同号,则Ty符号为正,否则Ty符号为负。最后,对于R,已知r1、r2、r4、r5,利用正交性和右手坐标系特性可计算R,有

式中,S=-sgn(r1r4+r2r5);r7,r8,r9可由头两行的叉乘得到。
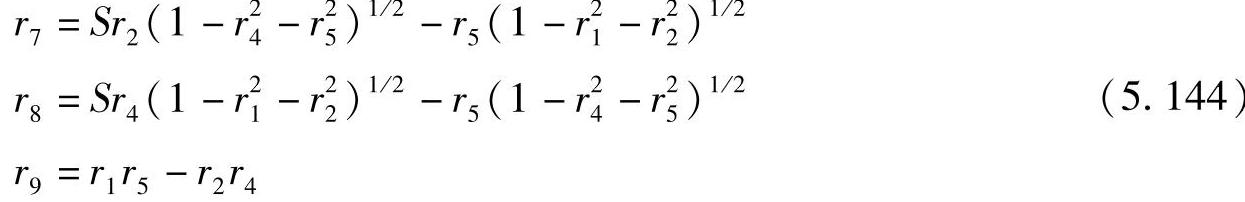
给定r1、r2、r4、r5,则R有两个解,另一个为
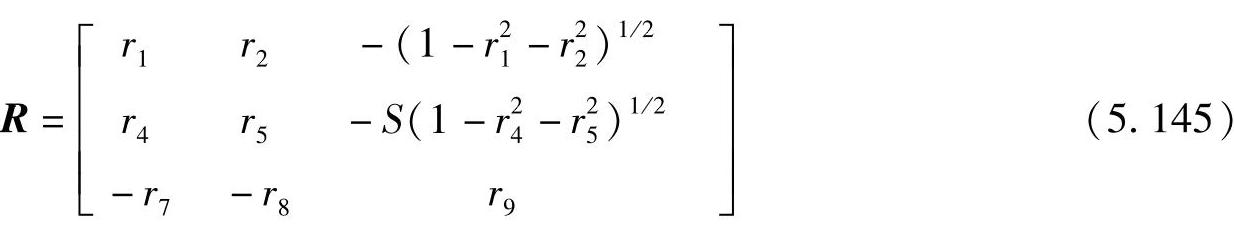
具体选择哪一个,可由试探法确定。即先任选一个,向下计算,若据此R值计算出的f<0,则此次选取不对,应选取另一个R的解。否则若f>0,则选取正确。
第二步:计算有效焦距f、T的Tz分量和透镜畸变系数k。

待求变量是f、k、Tz,假设

可得

对N个特征点,利用最小二乘法对上述两个方程进行联合最优参数估计,进一步求得f、fk、Tz,进而求得f、k、Tz。
相关文章

不考虑摄像机镜头的非线性畸变,那么从物体点的三维到图像点的二维变换是线性变换,透视变换中的系数为未知数。以上介绍了摄像机标定的透视变换法的计算过程,在用真实数据进行实验时,需要注意以下问题:1)矩阵M确定了空间点坐标与它的图像点坐标的关系。......
2025-09-30

周富强 邾继贵 杨学友 叶声华摘要:在视觉检测系统中,针对视觉传感器数量多,且每个摄像机需标定的内部参数及外部参数较多的特点,提出了一种新的简单的快速摄像机标定方法。分析了摄像机的各个关键参数,采用了全线性标定方法和矢量分析法,逐步求出CCD摄像机的参数。实际结果表明,摄像机标定误差优于0.05mm。......
2025-09-29

其中,直接线性变换是最优化算法,两步法进一步考虑了畸变补偿,双平面法合理运用了摄像机的成像模型。3)将各标定点相应的像平面坐标(u,v)及世界空间坐标代入摄像机模型式中,根据标定方法,求解摄像机内外参数。......
2025-09-30

多数情况下,这些参数必须通过实验与计算才能得到,这个过程称为摄像机的标定。摄像机标定一般分为经典标定方法和自标定方法。当前对传统摄像机标定技术的研究集中在非线性畸变校正。自标定方法不依赖于标定参照物,仅利用摄像机在运动过程中周围环境的图像与图像之间的对应关系对摄像机进行标定。图5.1 摄像机标定系统图5.2 标定靶标的控制点类型......
2025-09-30

图2-23 ELO 2S在不同生长阶段的横截面。两级ELO技术开始于这样一种生长条件,即促使垂直生长快于横向生长,使晶粒的横截面为完美的三角形。图2-24a所示为一个GaN锥横截面的TEM图。图2-24 平面的横截面TEM图像显示出一个GaN锥及其示意图注:虚线表明了不同生长阶段的晶体。ELO 2S GaN表面的阴极射线致发光图像显示出因介质掩膜的图2-25 用ELO 2S方法生长的GaN表面CL图像注:白色箭头标出了介质上方的聚结边界。ELO 2S层的平均位错密度约为5×107/cm2。......
2025-09-29

移动的基本步法有垫步、交叉步、小碎步、并步、蹬转步、蹬跨步和腾跳步等。视对方来球距离的远近,前场、中场和后场等各项步法可选用一步、两步或三步移动步法到位击球。(四)上网步法上网步法是完成上网搓球、推球、勾球、扑球及挑球的步法,它包括蹬跨步上网,垫步加蹬跨步上网,前交叉步加蹬跨步上网,后交叉步加蹬跨步上网、蹬跳步上网等。正手后退步法包括侧身后退一步步法、侧身并步退步法和交叉步后退步法。......
2025-09-30

配制一系列不同浓度的NaCl和Na2 SO4混合溶液,并测出其电导率,列于表2。表2中A组为NaCl和Na2 SO4大浓度范围的混合液,全盐量浓度为50~2000mg/L。建立三组实验数据全盐量和电导率的线性关系和乘幂关系,将得到的线性回归方程和乘幂回归方程列于表3。表2浓度范围对关系曲线的影响单位浓度:mg/L;电导:μS/cm表3不同浓度范围下各回归方程的比较注表中x表示电导率,μS/cm;y表示全盐量mg/L。......
2025-09-29

在汽车工业中,非织造布的抗静电性能检测主要考核项目有电阻、电压、静电压半衰期、带电量等项技术指标。在满足上述两个条件的前提下,采用下述两步法可以实现线结构光传感器对空间圆(类圆)孔中心位置的测量。两步法测量基本原理如下。......
2025-09-29
相关推荐