图5.17 直接光学法确定图像中心的标定原理4）基于中心无畸变区的摄像机光学中心标定方法 基于中心无畸变区的摄像机光学中心标定方法利用的是透视成像的基本原理。求解光学中心的矩阵表达式对式和式用最小二乘法求解，便可得到模板点的轨迹方程和光学中心坐标。给定r1、r2、r4、r5，则R有两个解，另一个为具体选择哪一个，可由试探法确定。......
2023-11-24
免费教程：用2步法轻松实现摄像机标定
【摘要】：先利用线性变换方法或透视变换方法求解摄像机参数，再以求得的参数作为初始值，考虑畸变因素，利用非线性优化方法进一步提高标定精度，就形成了所谓的两步法。两步法计算量适中、精度较高。摄像机坐标系定义为原点在摄像机光学中心，z轴与光轴重合。
摄像机非线性模型除包括线性模型中的全部参数外，还包括非线性径向畸变参数k1、k2和切向畸变参数p1、p2。线性模型的参数和非线性模型的参数一起构成了非线性模型的摄像机内部参数。
非线性模型求解是由非线性优化方法来估计，如广泛采用的Levenberg Marquardt（LM）优化算法和Newton Raphson（NR）优化算法。这些方法都涉及非线性方程求解，或需假设摄像机部分内参数可由其他方法测出；或者用线性模型首先计算出线性模型的参数，作为近似初值，再用迭代方法计算精确解。
针对三维立体靶标上的特征点，用线性模型首先计算出线性模型的参数，作为近似值，再用迭代的方法计算精确解，是非线性模型摄像机标定较为有效的方法。
先利用线性变换方法或透视变换方法求解摄像机参数，再以求得的参数作为初始值，考虑畸变因素，利用非线性优化方法进一步提高标定精度，就形成了所谓的两步法。
典型两步法是基于径向排列约束RAC的两步法：第一步是利用最小二乘法解超定线性方程，求得外部参数；第二步求解内部参数，先假定摄像机无镜头畸变，求解超定线性方程组给出初值。再结合非线性优化方法获得全部参数。两步法计算量适中、精度较高。
1.两步法采用的摄像机模型
如图5.16所示，设（X，Y，Z）是三维世界坐标系中某目标点P的三维坐标。摄像机坐标系定义为原点在摄像机光学中心，z轴与光轴重合。（x，y，z）是同一点P在摄像机坐标系中的三维坐标。x′o′y′是原点在光轴z与图像平面的交点o′点平行于x，y轴的像平面坐标系。有效焦距f是图像平面和光学中心的距离。（x′，y′）是小孔成像模型下世界坐标点P的像平面坐标。（x*，y*）是由于摄像机镜头畸变引起偏移的实际像平面坐标。（u，v）是以像素为单位的图像坐标。（u0，v0）是像主点坐标。与前文类似，从点P世界坐标（X，Y，Z）通过投影变换映射为图像坐标由以下步骤完成。
（1）由世界坐标系到摄像机坐标转换
式中，R为3×3旋转矩阵，T为3×1平移矩阵。
（2）成像变换
（3）畸变模型
造成成像坐标偏差畸变有径向畸变、偏心畸变和薄棱镜畸变。只考虑径向畸变并用二阶多项式近似描述径向畸变，有
理想像平面坐标和实际像平面坐标的关系如下：
式中，k为径向畸变系数。
（4）实际像平面坐标到图像坐标的转换
式中，μ为尺度因子；Sx′=SxNcx/Nfx为像素行方向的等效间距。所谓等效间距是指相邻两个像素对应的CCD阵列中的感光单元间距。假定CCD感光阵列行相邻单元间距为Sx，CCD每一行的感光单元个数为Ncx。从感光阵列到像素阵列的处理过程如下：图像获取硬件首先对每一行感光单元利用零阶采样保持器获得模拟波，然后再对该波进行采样，得到一行Nfx个像素。这样理想情况下像素行方向上的等效距离为Sx′=SxNcx/Nfx，由于图像扫描是逐行进行的，像素列方向上的等效间距与感光阵列列方向的实际间距相同，均为Sy。
通常情况下，CCD生产商提供的Sx、Sy可以达到亚微米精度，Ncx和Nfx对于特定CCD和图像采集卡为已知值，进而Sx′、Sy均为已知值。但在实际情况下，图像获取硬件和摄像机扫描硬件间存在的同步差或摄像机硬件本身时钟的不精确会造成一些不确定因素，直接影响像素行方向的等效间距值，因此引入尺度引子μ来表示这种不确定性。(www.chuimin.cn)
2.两步法原理
摄像机标定中，需标定外部参数6个，内部参数6个，即u0、v0、Sx′、Sy、f、k。其中，u0、v0、Sx′、Sy通过预标定确定。采用两步标定法，可以先求解外部6个参数，再计算2个内部参数。
图5.16 摄像机成像示意图
根据摄像机成像模型，理想的透视投影关系如图5.16所示。空间点P（X，Y，Z）在摄像机像平面上的理想像素点为p′（x′，y′），由于摄像机镜头的径向畸变，实际像素点为p*（x*，y*）。它与P（X，Y，Z）之间不符合投影透视关系。
由图5.16可以看出，
与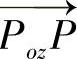
的方向一致，
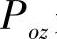是摄像机光轴上的一点，其z坐标与物点在摄像机坐标系下的坐标值相同。
1）假设摄像机镜头畸变只是径向的，那么无论畸变如何变化，从图像中心点o′到图像点p*（x*，y*）的矢量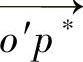
的方向将保持不变，并且
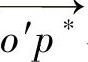与
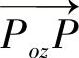平行。
2）摄像机的等效焦距f对x*，y*产生同样的影响，f的大小不影响矢量
的方向。
3）世界坐标系沿着x*轴和y*轴放置和平移，使得每一点有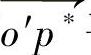
平行于
，对x*，y*产生的影响相同，从而o
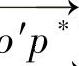的方向保持不变。
4）在每一点处矢量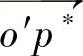
与
的平行约束条件，与径向畸变表达式的系数、等效焦距f、平移分量Tz无关。而R和Tx、Ty受该约束制约。
因此，运用径向排列约束，存在如下关系：
设
根据坐标转换公式，则
根据RAC含义，有
整理得
行矢量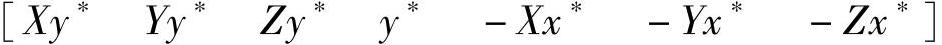
是已知的，由标定模板和图像处理确定，列矢量
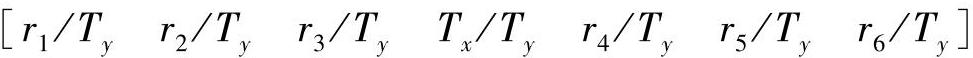是待求参数。
对每一标定模板目标点Pi，已知其X、Y、Z、x*、y*就可以列出如上的一个方程。R有9个参数，但是其正交性规定了R仅有三个自由度，再加上Tx、Ty正好五个独立变量，故上式可惟一确定旋转矩阵R和Tx、Ty。
求出R和Tx、Ty后，再利用最优化方法求解有效焦距f、T的Tz分量和透镜畸变系数k。
有关视觉测量技术的文章
- 详细阅读
-
数学思维技巧：用2页图解帮你轻松理解详细阅读
我们可以通过映射来建立集合间的联系。我们可以通过图解来表示映射，其中一边是集合A中的元素，另一边是集合B中的元素，用箭头将集合A与集合B中的元素相连。参考阅读//No. 7 集合论，第18页No. 13 范畴，第30页右图：由列奥纳多的《最后的晚餐》中的人物到他们在《约翰福音》中的名字的映射。......
2023-11-22
-
摄像机标定-双平面法详细阅读
利用这些转换系数，图像平面上的任意一点P，都可以在两个参考平面上找到点P1、P2与之对应。通过式连接P1、P2，可得到点P的视线，有了视线方向，便可以很容易地进行立体三角测量。......
2023-11-24
-
2页纸图解数学：轻松读懂数学的三步法详细阅读
19世纪90年代，大卫·希尔伯特证明出一个结果，它被称为“零点定理”，这个定理用精准的术语对这一对应关系做了探讨。这就是零点定理的核心，也是代数几何成立的条件。和代数拓扑类似，代数几何的核心在于，我们已经对环的性质有了许多了解，所以把簇“翻译”成环的语言处理，要比直接处理更方便。零点定理为代数几何的建立提供了基本词典。......
2023-11-22
-
摄像机标定的透视变换法详细阅读
不考虑摄像机镜头的非线性畸变，那么从物体点的三维到图像点的二维变换是线性变换，透视变换中的系数为未知数。以上介绍了摄像机标定的透视变换法的计算过程，在用真实数据进行实验时，需要注意以下问题：1）矩阵M确定了空间点坐标与它的图像点坐标的关系。......
2023-11-24
-
快速标定CCD摄像机的技巧详细阅读
周富强 邾继贵 杨学友 叶声华摘要：在视觉检测系统中，针对视觉传感器数量多，且每个摄像机需标定的内部参数及外部参数较多的特点，提出了一种新的简单的快速摄像机标定方法。分析了摄像机的各个关键参数，采用了全线性标定方法和矢量分析法，逐步求出CCD摄像机的参数。实际结果表明，摄像机标定误差优于0.05mm。......
2023-06-23
-
2页纸图解数学：用智慧方式，轻松学习数学详细阅读
欧拉将哥尼斯堡的地图简化为七条边连接起四个点，其中每一个点都代表一块陆地，每一条边都代表一座桥。图论研究的就是事物连接在一起的方式。参考阅读//No. 70 拓扑，第144页No. 71 三角剖分，第146页No. 93 组合学，第190页No. 100 P 与NP，第204 页右图：一个图有八种不同的嵌入方式。......
2023-11-22
-
摄像机标定的原理、方法及结果详细阅读
其中，直接线性变换是最优化算法，两步法进一步考虑了畸变补偿，双平面法合理运用了摄像机的成像模型。3）将各标定点相应的像平面坐标（u，v）及世界空间坐标代入摄像机模型式中，根据标定方法，求解摄像机内外参数。......
2023-11-24
相关推荐