多数情况下,这些参数必须通过实验与计算才能得到,这个过程称为摄像机的标定。摄像机标定一般分为经典标定方法和自标定方法。当前对传统摄像机标定技术的研究集中在非线性畸变校正。自标定方法不依赖于标定参照物,仅利用摄像机在运动过程中周围环境的图像与图像之间的对应关系对摄像机进行标定。图5.1 摄像机标定系统图5.2 标定靶标的控制点类型......
2025-09-30
摄像机模型即描述空间点与其成像点之间关系的公式。根据所定义的世界坐标系、摄像机坐标系等几个坐标系之间的相互关系不同,可以得到不同的摄像机成像几何模型。
1.世界坐标与摄像机坐标重合时的摄像机模型
(1)投影变换
如图5.10所示,应用小孔成像模型,图像中摄像机坐标系统的xy平面与像平面重合,光学轴沿z轴。这样像平面的中心处于原点,镜头光学中心的坐标是(0,0,f),f是镜头的焦距。假设摄像机坐标系统与世界坐标系统XYZ平行。
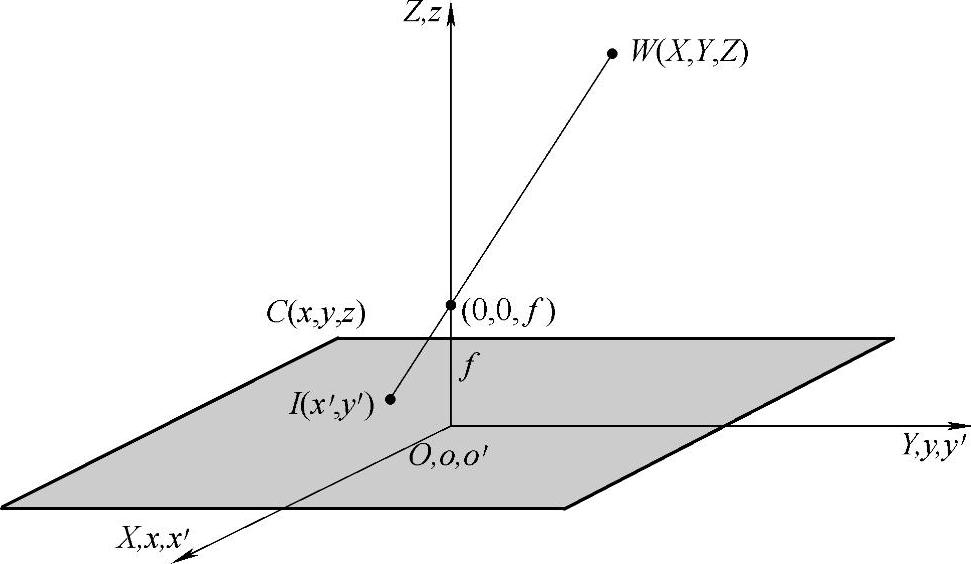
图5.10 投影成像
设(X,Y,Z)是三维空间中任意点W的世界坐标。以下讨论都假设Z>f,即所有客观场景中感兴趣的点都在镜头前面。第一步要建立点W(X,Y,Z)与其投影到图像平面的坐标间的联系,借助相似三角形得到

式中,X和Y前的负号表示图像像点反转了。由式(5.36)可得到三维投影后的图像平面坐标

这些等式是非线性的,因为它们分母中含变量Z。可以借助齐次坐标将它们表示成线性矩阵的形式。
空间一个点对应的笛卡儿坐标XYZ的齐次坐标定义为(kX,kY,kZ,k)。其中,k是任意非零常数。将齐次坐标变回笛卡儿坐标可用第4个坐标量去除前三个坐标量得到。这样一个笛卡儿世界坐标系统中的点的矢量形式为

对应的齐次坐标为

定义透视变换矩阵为

P和Wh的乘积给出了一个矢量ch,即
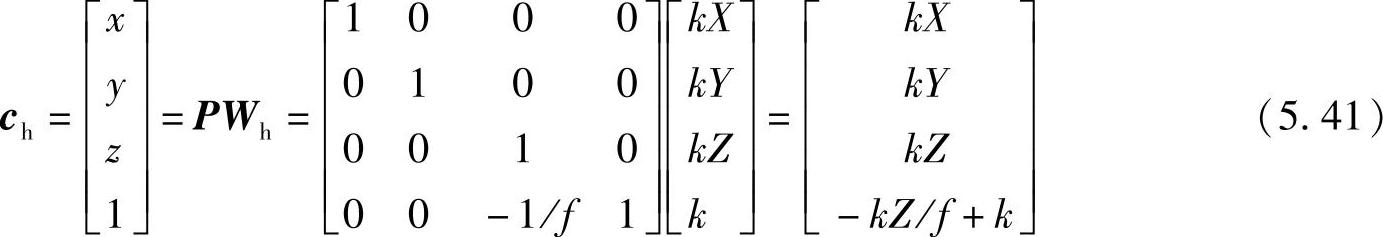
ch的元素是齐次形式的摄像机坐标,这些坐标可用ch的第四项分别去除前三项转换成笛卡儿形式。所以摄像机坐标系中任意点笛卡儿坐标可表示成矢量形式,即
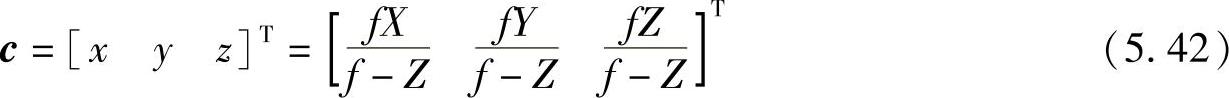
式中c的前两项是三维空间点(X,Y,Z)投影到图像平面后的坐标(x,y),第三项在图5.10所示的模型中无用,但表示投影变换物点与像点的比例关系,在逆投影变换中可以起到自由变量的作用。
(2)逆变换
逆投影变换将一个图像点反过来映射回三维空间。从式(5.41)可以得到

其中

在逆投影变换中,不能由像坐标求出三维空间点坐标,其本质原因是由于三维客观场景映射到像平面是多点对一点的变换。像点的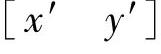 对应于过
对应于过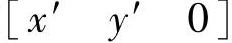 和
和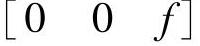 的直线上的所有共线三维点的集合。这条线的方程在世界坐标系可由式(5.42)得到,即
的直线上的所有共线三维点的集合。这条线的方程在世界坐标系可由式(5.42)得到,即

式(5.45)表明除非对产生图像点的三维空间点有一些先验知识(如知道Z坐标),否则不可能将一个三维点的坐标从它的图像中完全恢复过来。
借助这一结论,用ch的z′项作为一个自由变量建立逆透视变换,设

根据式(5.43)有
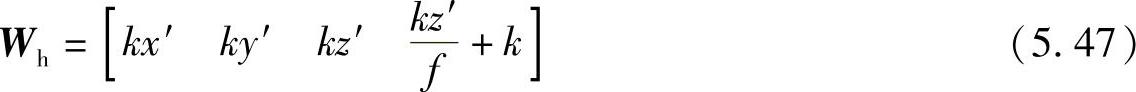
转换成世界坐标为
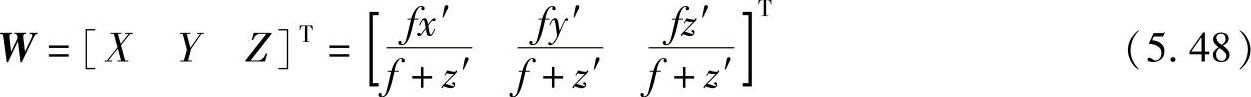
换句话说,把z′作为自由变量可以得到以下三个等式:

如果在最后一式中用Z解出z′,代入前两式可以得到

(3)结论
投影变换是三维空间的一条射线上的所有点,对应图像平面上的一个像点,空间一点可得惟一像点,而一个像点对应一条射线上的无数空间点。利用逆透视变换将三维空间点从其图像中恢复出来需要知道该点的至少一个世界坐标。
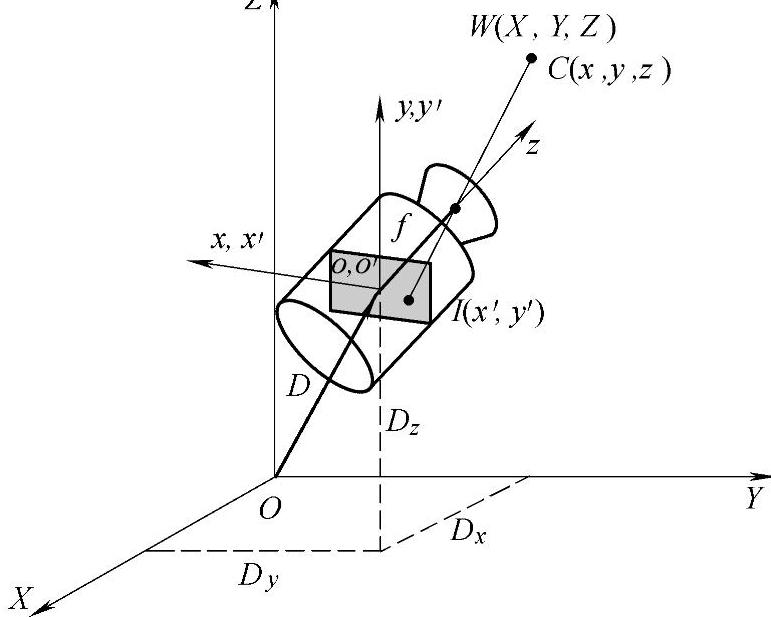
图5.11 世界坐标系与摄像机坐标系不重 合时的投影成像
2.世界坐标系与摄像机坐标分开时的摄像机模型
考虑更一般的情况,即摄像机坐标系和世界坐标系分开的情况,但仍将平面xy和像平面x′y′重合。此时摄像机坐标系代表了摄像机的位姿。
图5.11所示为这种情况下的摄像机几何模型,像平面中心(原点)与世界坐标系的位置偏差记为矢量D,其分量为Dx、Dy、Dz。假设摄像机分别以α、β、γ角度绕x、y、z轴转动,则坐标系平移矩阵为
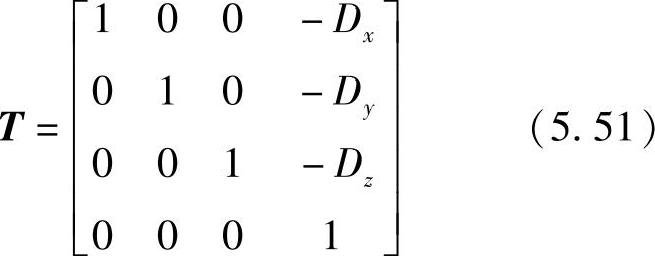
坐标系绕x转动α角,则坐标系旋转矩阵为

坐标系绕y轴转动β角,则坐标系旋转矩阵为(https://www.chuimin.cn)

坐标系绕z轴转动γ角,则坐标系旋转矩阵为

旋转矩阵的计算与旋转顺序有关,如以γ➝α➝β顺序旋转,即先绕z轴转动γ角。然后以新的坐标轴为基准,绕x轴转动α角。最后绕y轴转动β角。则旋转矩阵可写为
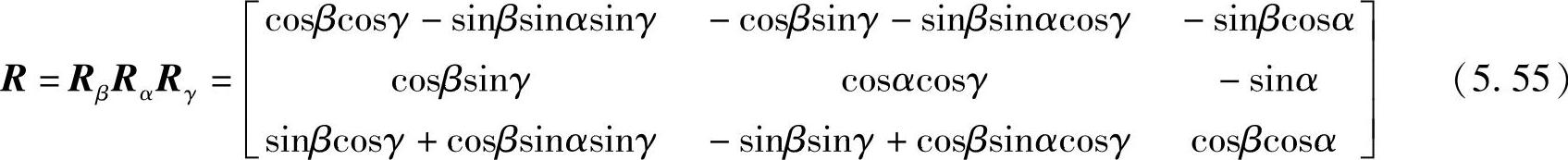
先作平移变换,再做旋转变换,将R并入平移矢量,则平移旋转矩阵为
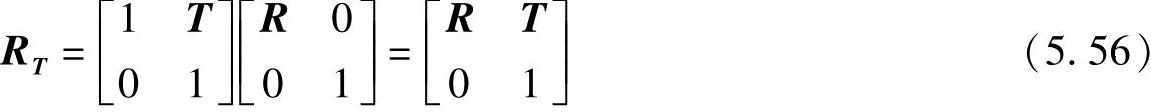
由此建立了世界坐标系和摄像机坐标系之间的变换关系为

此时,摄像机观察到的齐次世界点在摄像机坐标系中具有如下形式:

式中,Wh=[kXkYkZk]T为齐次世界坐标;P为透视变换矩阵;R和T表示的是摄像机的空间位置和朝向。这些参数称为外部参数。
3.通用摄像机模型
考虑更加一般的情况,即世界坐标系、摄像机坐标系和像平面坐标系都不重合。此外,还考虑如下两个因素:
1)摄像机镜头的畸变误差,像平面上的成像位置与前述线性变换公式计算出的透视变换投影结果有偏差。
2)计算机中使用的图像坐标单位是存储器中离散像素的个数,所以像平面上的连续坐标还需取整转换为离散坐标。
图5.12所示为考虑这些因素时的通用摄像机模型示意图。
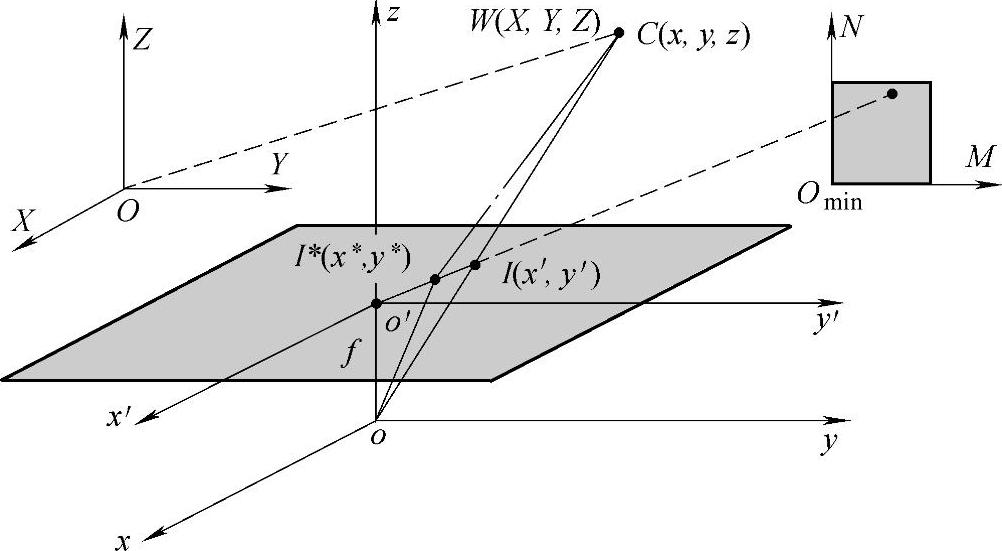
图5.12 通用摄像机模型示意图
如图5.12所示,摄像机坐标系的原点o位于摄像机的镜头中心,像平面坐标中心o′位于光轴上,由小孔成像模型,oo′=f,f为焦距。如图5.13所示,从客观场景到数字图像的成像变换可看作由以下4步组成:

图5.13 从客观场景到数字图像的成像变换步骤
(1)从世界坐标(X,Y,Z)到摄像机三维坐标(x,y,z)的变换由前述摄像机模型可知,变换可表示为

式中,R和T分别为3×3的旋转矩阵(两坐标系三组对应坐标轴间夹角的函数)和1×3的平移矢量。
(2)从摄像机三维坐标(x,y,z)到无失真像平面理想坐标(x′,y′)之间的变换有

将式(5.60)用齐次坐标形式与矩阵表示为
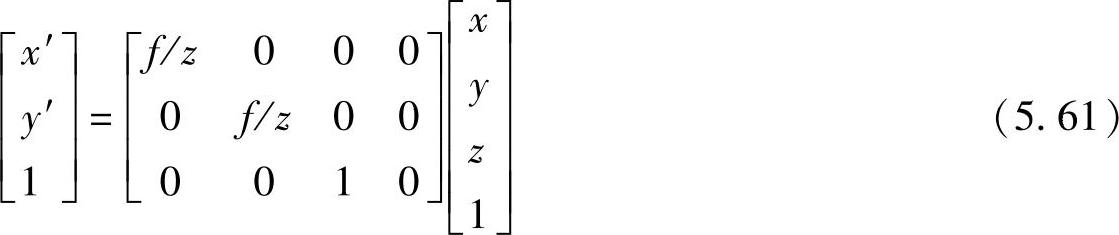
(3)从无失真像平面理想坐标(x′,y′)到受镜头畸变影响而偏移的实际像平面坐标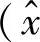 ,
,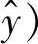 的变换
的变换
有

式中,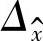 和
和 代表镜头畸变。
代表镜头畸变。
(4)从像平面坐标(x′,y′)到图像坐标(u,v)的变换(见图5.14)
1)图像坐标系 摄像机采集的数字图像在计算机内可以存储为数组,数组中每一个元素为像素。在图像上定义直角坐标系uv,每一像素坐标分别是该像素在数组中的行数和列数。所以,uv是以像素为单位的图像坐标系坐标。
2)像平面坐标系 图像坐标系是以像素为单位的坐标系,而像平面坐标系x′y′是连续坐标系,或物理单位坐标系。用(u,v)表示图像坐标,(x′,y′)表示像平面坐标,x′y′坐标系原点定义在摄像机光轴与图像平面的交点(u0,v0)处,称为像主点。在x′轴和y′轴方向上像素之间的距离为Sx和Sy。则两坐标系之间的关系为
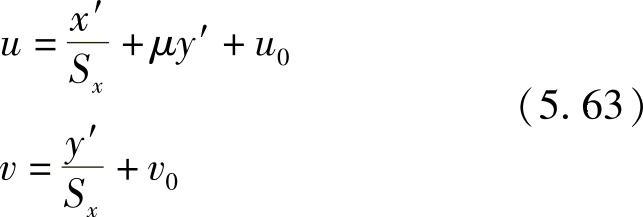
表示成矩阵形式
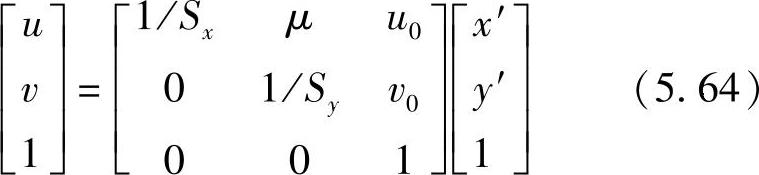
由于摄像机制造及工艺等原因,像素点可能发生畸变,μ定义为考虑像素点畸变的畸变因子,有时也称图像不确定因子、倾斜因子等。矩阵S称为内参数矩阵。
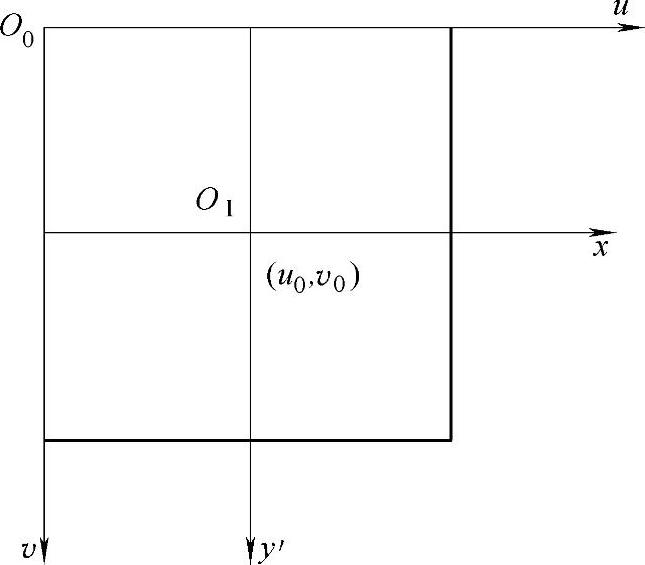
图5.14 图像坐标系与像平面坐标系
综上所述,当世界坐标、摄像机坐标、像平面坐标、图像坐标都分开且不考虑畸变影响时的通用摄像机模型可表示为

M1只与摄像机内部结构有关,称摄像机内部参数。主要包括x方向尺度因子f/Sx,y方向尺度因子f/Sy,像主点在图像坐标系中的坐标(u0,v0),畸变因子μ。M2只与摄像机相对于世界坐标系的方位有关,称为摄像机的外部参数。外部参数可以认为是12个,包括旋转矩阵R的9个参数和平移矩阵的3个参数;也可以定义为6个,包括旋转矩阵的3个偏转角和平移矩阵的3个参数。Wh为空间点在世界坐标系下的齐次坐标。摄像机标定过程如图5.15所示。
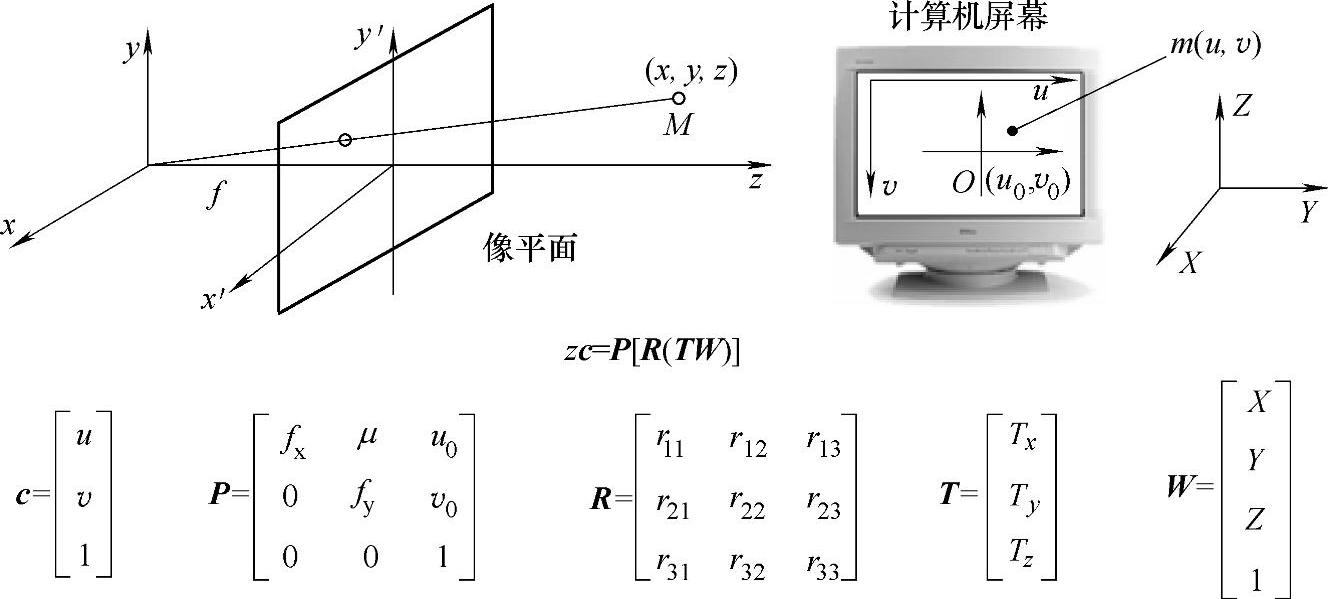
图5.15 摄像机标定过程
上述摄像机模型为线性模型,如果已知摄像机的内外参数,即矩阵M已知,对任何空间点,知道其世界坐标,就可以求出其图像像素坐标系中该图像点的坐标。反过来,如果已知空间某点的图像坐标,即使已知其内外参数,空间坐标也不是惟一确定的,它对应空间的一条射线。当考虑摄像机镜头畸变时,摄像机模型为非线性模型,有

相关文章

多数情况下,这些参数必须通过实验与计算才能得到,这个过程称为摄像机的标定。摄像机标定一般分为经典标定方法和自标定方法。当前对传统摄像机标定技术的研究集中在非线性畸变校正。自标定方法不依赖于标定参照物,仅利用摄像机在运动过程中周围环境的图像与图像之间的对应关系对摄像机进行标定。图5.1 摄像机标定系统图5.2 标定靶标的控制点类型......
2025-09-30

计算机视觉测量技术以图像传感器为手段检测空间物体的空间三维坐标,进而检测物体的尺寸、形状和运动状态等。美国、加拿大、日本等发达国家早在20世纪60年代后期就已经开始了计算机视觉测量技术的研究。直到20世纪90年代,随着计算机技术的发展成熟,计算机视觉测量技术逐渐成为一个研究热点。......
2025-09-30

下面简要介绍Marr视觉理论的基本思想和框架。图1.1 Marr视觉信息处理的三个阶段第一阶段是早期视觉处理,其目的是从输入的原始图像中抽取观察者周围景物表面的物理特性,如距离、表面方向、材料特性等,并构成要素图或基元图。表1.2 由图像恢复形状信息的表达框架3.Marr视觉理论的意义及不足Marr视觉理论是计算机视觉研究领域的划时代成就。图1.2 改进后的Marr视觉理论框架限于历史等因素,Marr没有研究如何用数学方法严格地描述视觉信息的问题。......
2025-09-30

在工业生产中,计算机视觉技术可以自动检测各种机械零件的几何尺寸,测量其精度范围,目前已经用于产品外形检验、表面缺陷检验等。2)利用计算机视觉技术进行病虫害的监测。在现代战争中,无人机发挥着举足轻重的作用。无人机导航是无人机技术的重要组成部分,基于计算机视觉的无人机导航技术是目前无人机导航领域的研究热点。......
2025-09-30

实验表明,描述摄像机成像的线性模型在很多情况下不能准确描述成像的几何关系,尤其在使用广角镜头时,远离图像中心处会有较大的畸变。图5.7 光学畸变2.畸变误差模型光学镜头畸变是视觉测量涉及的主要像差,高精度测量时,进行摄像机标定必须考虑镜头畸变。其数学模型为式中,s1和s2为薄棱镜畸变系数。......
2025-09-30

在扫描过程中,如果发现某个像素的灰度值由0变为1且没有分配标记,则给该像素分配一个没有使用的标记;如果当前正被扫描的像素值为1,则根据其与邻域像素的连通性对其进行标记;如果当前像素与多个目标相连通,则可以认为这些目标实际上是同一个,并把它们连接起来。......
2025-09-30

成像系统的几何畸变误差是典型的系统误差,是影响光学测量精度的因素之一。选用高质量的镜头和进行镜头畸变校正可提高测量精度。......
2025-09-30
相关推荐