最小类内方差法在视觉测量技术中的应用

2025-09-30 理论教育版权反馈

【摘要】：最小类内方差法也称为均匀性度量法。下面以两个区域为例来分析基于多次尝试的最小类内方差法。6）挑选最小类内方差所对应的阈值，即T*为可见最小方差法是一种自动阈值选择方法，整个过程不需要人工设定其他参数。

当图像直方图无明显的双峰，或双峰低谷都不明显，而且各个区域的面积又不可知时，可以采用最大方差自动阈值法来获取满意的阈值。最小类内方差法也称为均匀性度量法。其设计思想是，在最佳阈值下，分割后的目标内部各个像素之间的性质应该最为接近。区域内的像素性质的相似程度可以用类内方差（例如同一个区域内像素的灰度方差）来衡量。为了寻找最小类内方差所对应的阈值，可以采用多次尝试的方法来寻找最佳阈值。下面以两个区域为例来分析基于多次尝试的最小类内方差法。

假设j表示阈值尝试的次数，当前阈值记为T^（j），初始时j=0，则最小方差法的基本步骤如下：

1）假设当前阈值为T^（j），并将图像分为C₁^（j）和C₂^（j）两个区域，即

2）计算两个区域中的像素百分比p_i^（j）

式中，N为图像中像素的总数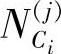；为第j次阈值分割中区域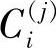的像素个数。

3）分别计算两类的均值和方差(https://www.chuimin.cn)

4）计算总体类内方差

5）令j=j+1，返回步骤1）尝试其他阈值，并根据1）～4）计算两类的方差。

6）挑选最小类内方差所对应的阈值，即T为

可见最小方差法是一种自动阈值选择方法，整个过程不需要人工设定其他参数。它不单适用于两个区域的分割，也可以扩展到多区域分割中去。

假设当前的一系列阈值为T_i^（j），将图像分割成n个区域S₀，S₁，…，S_n-1。其中，j表示尝试次数，i表示第几个阈值，σ²_i（j）表示第j次迭代过程中第i个区域的方差。那么基于最小方差的多区域分割算法基本步骤与基于最小方差的2区域分割算法基本类似，只需对1）和4）做一点变动。其中，1）应当根据式（4.92）完成图像的分割，4）的总体方差计算应该根据下式进行：

最小类内方差法在视觉测量技术中的应用

相关推荐