视觉测量技术中的边缘点检测及多尺度算法

边缘检测的算法很多，说明如下。

（1）空域微分算子法

这也是传统的边缘检测算法。由于边缘是图像上灰度变换最为剧烈的地方，因此函数梯度变化大的地方就是边缘。传统的边缘检测算子正是利用这个特点，对图像中的各个像素求一阶或二阶导数来确定图像的边缘点。其中，一阶微分图像的峰值点对应着图像的边缘，二阶图像的过零点对应着图像的边缘点。目前，已经提出了各种各样的空域微分算子，例如Robert算子、Sobel算子、拉普拉斯算子等典型的梯度算子。

（2）曲面拟合法

利用当前像素邻域中的一些像素拟合一个曲面，然后求这个连续曲面在当前像素处的梯度。

（3）小波多尺度检测

利用多种尺度的边缘检测算子对图像进行检测，然后综合它们的检测结果以获得理想的输出。通常，小尺度参数的检测算子能够检测出灰度的细微变换，反映更多的边缘细节，定位精度较高，但对噪声比较敏感。而大尺度参数的检测算子能够检测出灰度的粗变换，反映大的边缘轮廓，对噪声不敏感，但是定位精度较差。因此，在多尺度边缘检测中，充分发挥大、小尺度各自的优势，对各种尺度上的边缘图像进行综合，就可以得到精确的图像边缘。

（4）基于数学形态学的边缘检测

数学形态学是一种有代表性的非结构数学方法。数学形态学运算中物体形状集合与结构元素之间的相互作用，对边缘方向不敏感，并能在很大程度上抑制噪声和探测真正的边缘。目前，常见的基于数学形态学的边缘检测方法有，基于多尺度形态学的边缘检测、基于数学形态学多级平均的图像边缘检测、基于偏微分方程的形态学边缘检测、基于均衡化和数学形态学的组合边缘检测等。其中，空域微分算子法、曲面拟合法等属于经典的边缘检测算法。

基于多尺度的边缘检测与基于形态学的边缘检测则是近20年来迅速发展起来的新方法。下面主要介绍梯度算子法和曲面拟合法等经典的边缘检测算法和基于形态学和小波的边缘检测方法。

1.梯度算子

灰度不连续常可利用导数检测，一般常用一阶和二阶导数来检测边缘点。利用导数微分性质检测图像中的突变，主要关注图像中的恒定灰度区、突变的开头和结尾及沿灰度级斜坡的导数特征。这些数据类型的微分性质可以用来描述图像中的噪声点、边缘等特征。在边缘检测中，基于一阶和二阶微分定义的边缘检测方法要保证在灰度不变区域的微分值为零、在灰度阶梯或斜坡的起始点处微分值非零和沿斜坡面的微分值非零。

（1）数字图像微分定义

在数字图像处理中，一元函数表达的一阶微分的定义如下：

这里为了与二元图像函数f（x，y）求微分时的表达式一致，使用偏导数符号。对二元函数，将沿着两个空间轴处理偏微分。二元函数的二阶微分定义为

（2）梯度算子的计算

梯度算子即基于一阶微分的图像边缘检测方法。图像处理中基于一阶微分的边缘检测是通过梯度法实现的。对于图像函数f（x，y），在其坐标（x，y）上的梯度可表示为一个矢量，通过二维列矢量来定义，其中G_x，G_y分别为沿x方向和y方向的导数，即

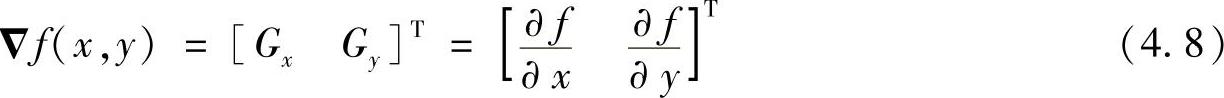
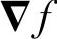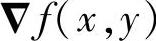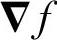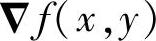由矢量分析可知，梯度矢量指向坐标（x，y）的f（x，y）的最大变化率方向。在边缘检测中，梯度矢量的大小用矢量模表示，给出了在方向上每增加单位距离后f（x，y）值增大的最大变化率。一般来讲，也将称为梯度。和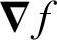交替使用梯度这一术语，但具体应用时应注意是指梯度矢量还是指梯度矢量的大小。

梯度矢量方向用方向角表示。令α（x，y）表示矢量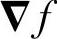在（x，y）处的方向角。梯度矢量的幅值和方向角分别为

这里角度以x轴为基准度量。边缘在（x，y）处的方向与该点的梯度矢量的方向垂直。式（4.9）幅度计算对应欧氏距离，也可对应其他距离来计算幅度，例如

1）幅度计算对应城区距离为

2）幅度计算对应棋盘距离为

虽然梯度矢量的分量是线性算子，但由于梯度模值用到了二次方和开方运算，因此梯度矢量的模值不是线性的。梯度矢量中的偏导数不是各向同性的，但梯度矢量的模值是各向同性的。对应城区距离的梯度计算简单且保持了灰度的相对变化，但各向同性特性较差，对水平和垂直边缘给出了相同的结果。

（3）梯度算子的计算模板

1）梯度模板 计算图像梯度是基于对在每个像素位置计算偏导数∂f/∂x，∂f/∂y。图4.12所示模板表示图像3×3区域的图像点。例如若中心点z₅表示f（x，y），那么z₁代表f（x-1，y-1），以此类推。那么采用上述模板计算一阶导数可表示为G_x=z₈-z₅，G_y=z₆-z₅。

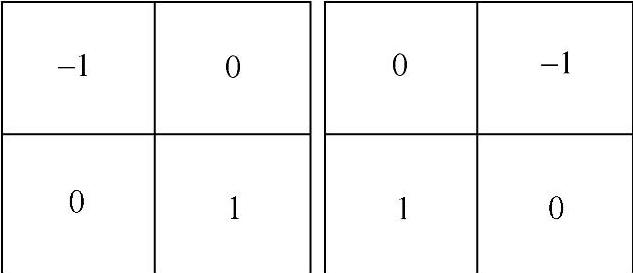
2）Robert交叉梯度算子 根据上述图像中导数计算的定义，导数计算可以采用交叉差分算法操作，即

G_x=z₉-z₅，G_y=z₈-z₆ （4.12）

上述计算即为Robert交叉梯度算子导数计算方法，可采用2×2尺度的模板（见图4.13）实现上述操作。

图4.12 计算模板

如果选取幅度，可以按下式计算梯度，即

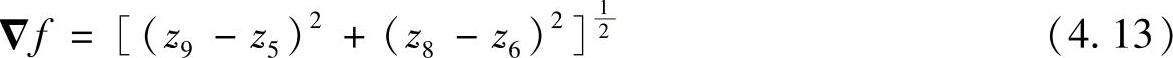
图4.13 Robert交叉算子

如果使用绝对值，按下式计算梯度：

3）Prittew算子 偶数模板不好用，2×2的模板没有明确的中心点。习惯上定义尺寸为3×3的最小模板，使用下式计算z₅点的导数：

G_x=(z₇+z₈+z₉）-（z_l+z₂+z₃ (4.15)

G_x=(z₃+z₆+z₉）-（z_l+z₄+z₇ (4.16)

3×3大小区域中的第一行和第三行间的差近似于x方向的导数，第三列和第一列之差近似于y方向上的导数。上述计算即为Prewitt算子导数计算方法。Prewitt算子导数计算可采用图4.14所示的两个模板。

可以按如下梯度模值和绝对值形式计算梯度：

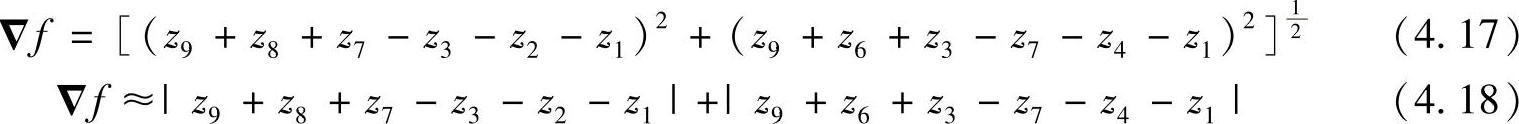
4）Sobel算子 改进上述Prewitt算子计算公式，在中心系数上使用一个权值2得到

G_x=(z₇+2z₈+z₉)-（z₁+2z₂+z₃) (4.19)

G_y=(z₃+2z₆+z₉)-（z₁+2z₄+z₇) (4.20)

在3×3图像区域中，第三行与第一行间的差接近于x方向的微分；第三列和第一列之差近似于y方向上的导数。使用权值2的目的是通过突出中心点的作用而达到平滑的目的。上述计算方法即为Sobel算子导数的计算方法，Sobel算子导数计算可采用图4.15所示的模板。

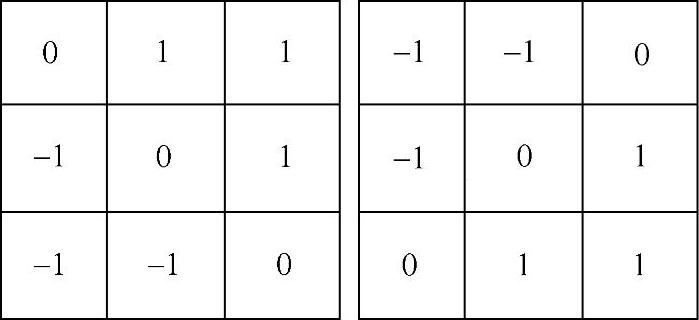
图4.14 Prewitt算子导数计算可采用的模板

图4.15 Sobel算子导数计算用的模板

如果选取幅度，可以按如下梯度模值和绝对值形式计算梯度：

5）梯度算子 对G_x，G_y各用一个模板，所以需两个模板组合起来构成一个梯度算子。常用的梯度算子有Robert算子、Sobel算子、Prewitt算子。各算子模板分别如图4.13、图4.14、图4.15所示。所有模板的系数和为零，表明在灰度恒定区的响应为零。

（4）拉普拉斯算子

拉普拉斯算子是二元函数的二阶微分在图像边缘检测中的应用，是二阶微分算子。一个二元图像函数f（x，y）的拉普拉斯变换定义为

拉普拉斯变换是线性操作。为适合图像处理，将方程表示为离散形式。通过邻域处理定义离散变换，根据二阶微分定义，在x方向上二阶偏微分采用下式定义：

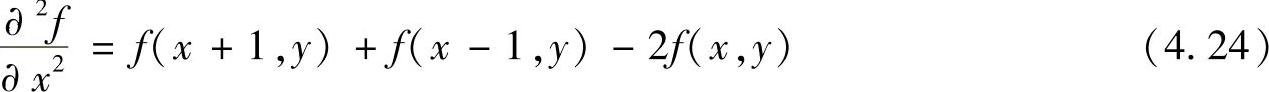
类似地，在y方向上有

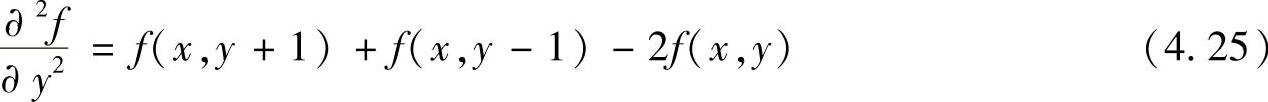
则拉普拉斯算子的数字实现可由这两个分量相加得到

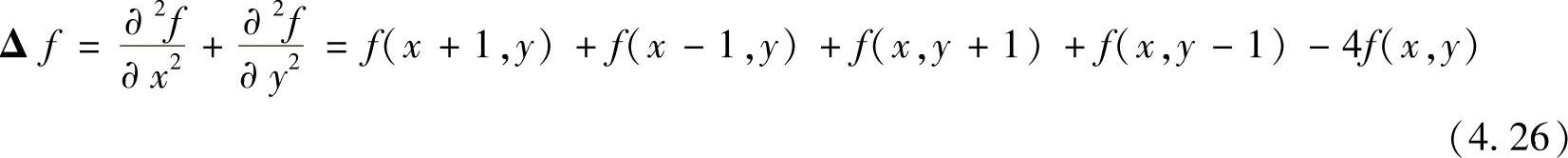
上述公式可用图4.16a所示模板实现。如图4.16b所示，对角线方向也可以加入到离散拉普拉斯变换定义中，即在定义式中添入两项，两个对角线方向各加入一项。由于每个对角线方向上的项还包含一个-2f（x，y），所以从不同方向项上减去的总和是-8f（x，y）。图4.16c所示的另两个模板实际中也经常使用。这两个模板以拉普拉斯变换定义为基础，其中的系数与图4.16a符号相反。上述模板的基本要求是对应中心像素的系数是正的，邻近像素的系数是负的，且所有系数的和是零，这样在灰度平坦区域响应为零。

拉普拉斯算子比前文所述的计算多个方向导数的梯度算子的计算量小。只需一个计算模板且不必综合各模板的值。

图4.16 拉普拉斯变换模板

1）拉普拉斯算子特点 拉普拉斯算子是一种各向同性的无方向性滤波器。这种滤波器的响应与图像的突变方向无关，各向同性（无方向性）滤波器是旋转不变的，即将原始图像旋转后进行滤波处理的结果与先对图像滤波，然后再旋转的结果相同。图4.16a、b所示模板对90°和45°的角度旋转是各向同性的。作为一个二阶导数，拉普拉斯算子对噪声比较敏感，对图像计算后会增强噪声，因此拉普拉斯算子一般不直接用于边缘检测。拉普拉斯算子的幅值产生双边缘。拉普拉斯算子不能检测边缘方向。由于上述原因，拉普拉斯算子在分割中常与平滑滤波器组合使用，利用其零交叉的性质进行边缘定位，也用来确定一个像素是在边缘暗的一边还是亮的一边。

2）拉普拉斯算子与平滑滤波组合使用 考虑函数

式中，σ为标准差。根据高斯滤波器特点，用一幅图像与该函数卷积会模糊该图像，图像的模糊程度是由σ值决定。h函数的拉普拉斯算子，即h关于x，y的二阶导数，即高斯函数的拉普拉斯算子

式中，r²=x²+y²。式（4.28）叫做高斯型拉普拉斯算子（LoG）。图4.17所示为LoG函数的三维曲线、图像、LoG函数的横截面和对Δh近似的5×5模板。模板系数总和为零。根据函数形状，高斯型的拉普拉斯算子有时也被称为墨西哥草帽函数。因为二阶导数是线性运算，所以用Δh卷积一幅图像与首先使用高斯型平滑函数卷积该图像，然后计算卷积结果的拉普拉斯算子效果相同。因此采用高斯型拉普拉斯算子卷积图像，相当于使用高斯型函数对图像进行平滑处理后，对图像采用拉普拉斯算子检测图像边缘。

图4.17 高斯型拉普拉斯算子（LoG）

（5）方向算子

方向算子利用一组模板分别计算在不同方向上的差分值，取其中最大的值作为边缘强度，而将与之对应的方向作为边缘方向。

1）Kirsch（3×3）模板

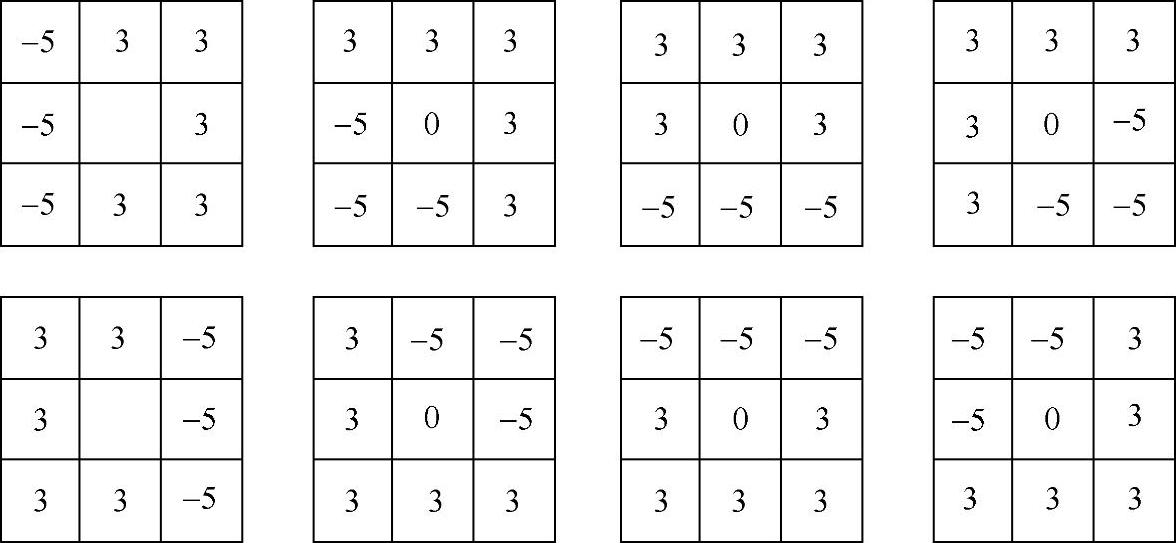
图4.18 Kirsch算子的八方向3×3模板

2）Nevitia（5×5）模板

2.曲线（曲面）拟合(www.chuimin.cn)

曲线（曲面）拟合就是用某个解析函数逼近实际数据。其基本思想是，用一个平面或曲面去逼近一个图像面积元，然后用这个平面的梯度或曲面的梯度替代点的梯度，从而实现边缘检测。可见，曲面或曲线的函数表达式的确定及图像面积元的选择均是曲线（曲面）拟合的关键。常用的面积元有图4.20所示的4点面积元和9点面积元两种。

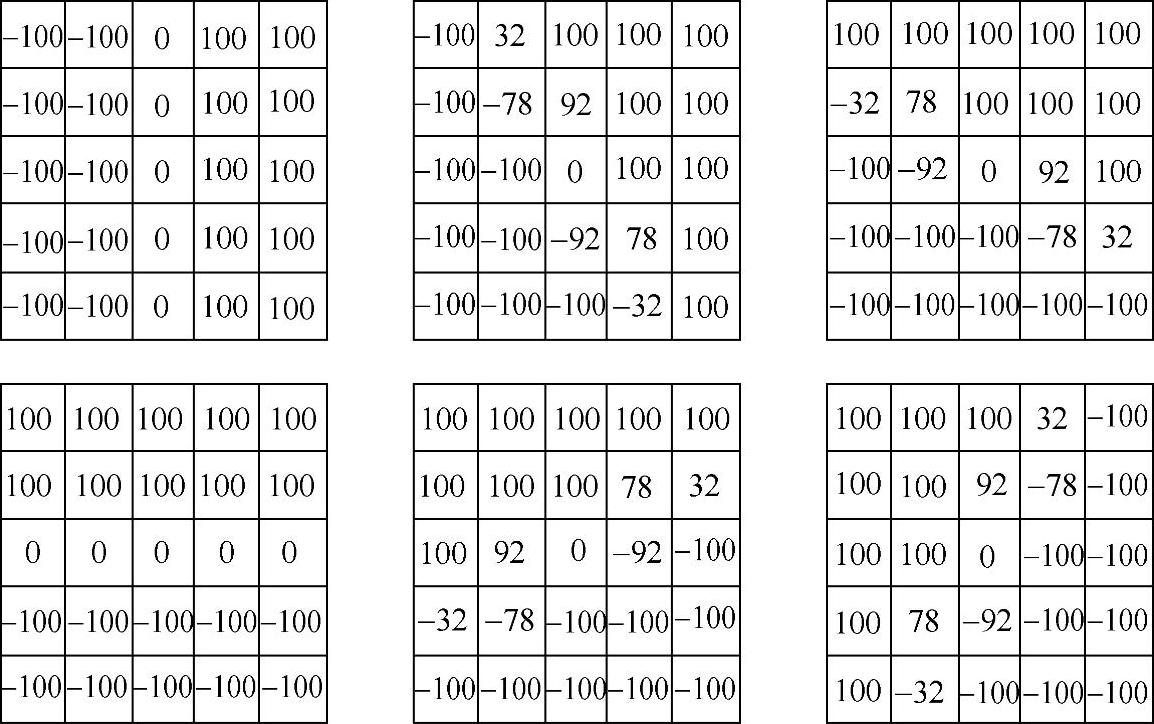
图4.19 Nevitia算子的十二方向5×5模板

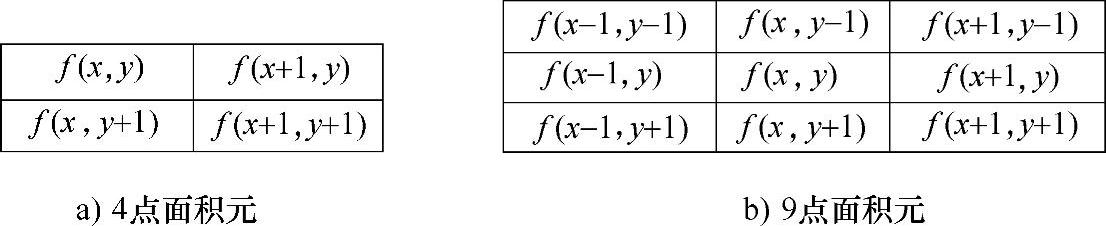
图4.20 曲面（曲线）拟合中常用的两种面积元

常用的曲面表达是一次平面拟合和二次曲面拟合两种表达式。

（1）一次曲面拟合

一次平面拟合就是用函数的一次表达形式拟合一个图像面积元f（x，y），即

g（x，y）=ax+by+c （4.29）

如果图像面积元由图4.20a所示的4个像素组成，那么f（x，y）和g（x，y）之间的方均误差为

目标是寻找最佳的参数a、b和c，从而使g（x，y）与f（x，y）之间的方均误差ε最小。为此需要对式（4.30）中的a、b和c分别进行求导并令导数为0，最后通过联立三个方程来求解a、b和c三个参数。首先，对式（4.30）进行求导，可以得到如下三个表达式：

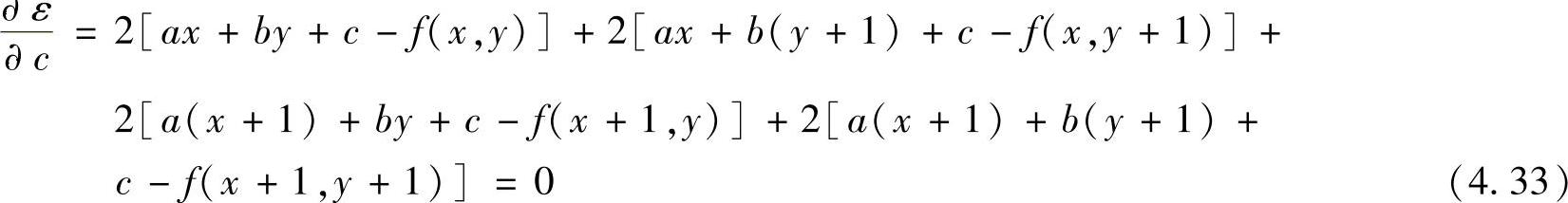
联立式（4.31）～式（4.33），可以计算出a、b和c的解为

从式（4.34）和式（4.35）可以看出，a是两行像素平均值的差分，b是两列像素平均值的差分。所以这种方法对噪声不敏感。根据梯度的定义，平面ax+by+c上的梯度幅度为

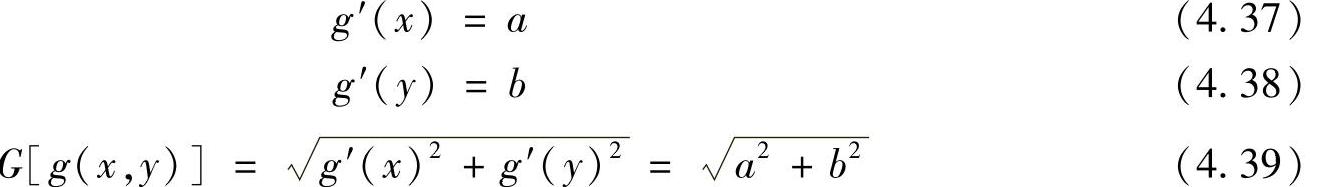
或

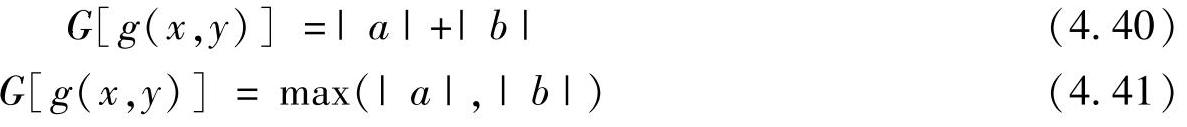
由于这个平面是对已知的2×2平面的最好近似，故可以把该平面的梯度看作是该邻域中心处图像梯度的近似值。

如果图像元面积元由图4.20b所示的9个相邻像素组成，则f（x，y）和g（x，y）之间的方均误差为

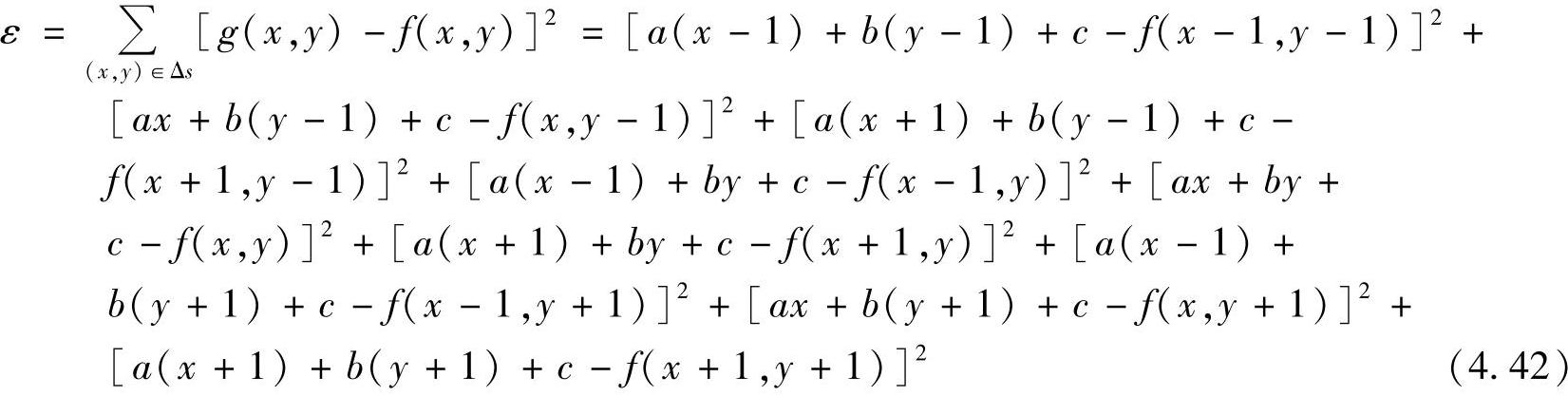
将式（4.42）对a、b和c进行求导并令导数为0，即

求解式（4.43），就可以得到a、b和c的解为

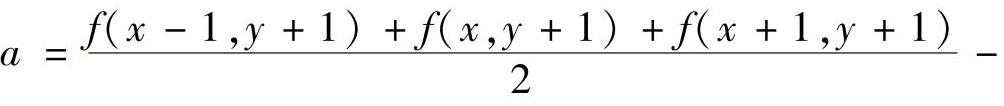
然后将a、b的值代入式（4.37）～式（4.41）计算位置[x，y]的梯度值。

（2）二次曲面拟合

设检测像素所在的面积元为图4.20a所示，用二次曲面

g(x,y)=ax²+bxy+cy²+dx+ey+k (4.47)

去拟合f（x，y），并产生方均误差

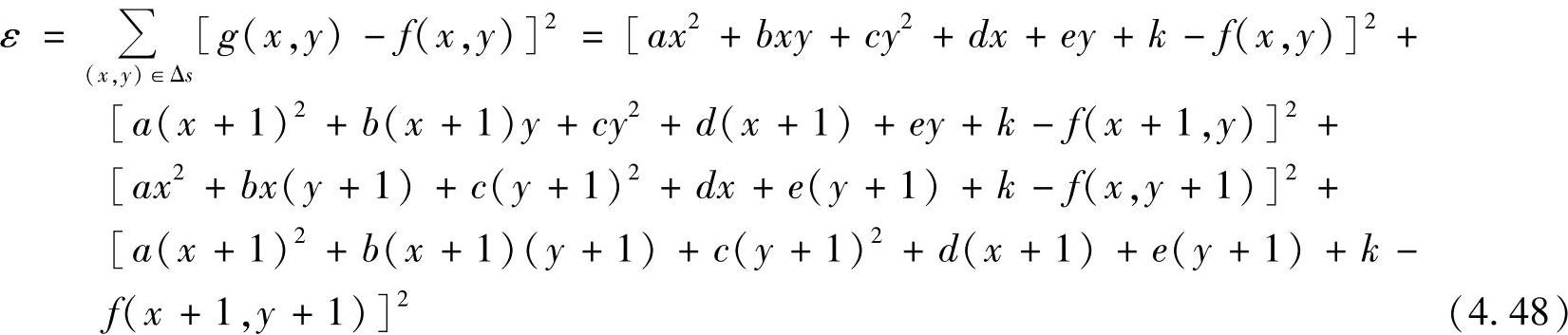
将式（4.48）对a、b、c、d、e和k六个参数分别进行求导并令导数为0，最后联立式（4.49）所示的6个方程组成的方程组，就可以推导出a、b、c、d、e和k的表达式，有

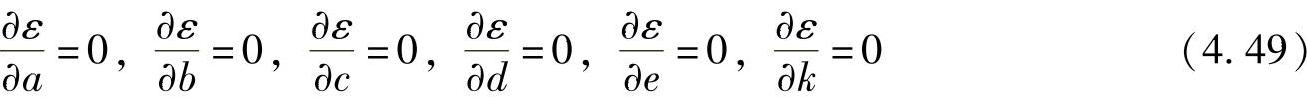
这里推导过程从略。在分别求出六个参数后，计算曲面在[x，y]的梯度为

g＇（x）=2ax+by+d (4.50)

g＇(y)=2cy+bx+e (4.51)

然后将梯度带入式（4.37）～式（4.41）计算其梯度幅度。

3.结合特定理论工具的图像边缘检测

（1）基于数学形态学的边缘检测

对某些强噪声图像，数学形态学运算可能取得好的效果。常用的边缘检测算子通过计算图像中局部小区域的差分来工作。这类边缘检测器或算子都对噪声比较敏感，并且常会在检测边缘的同时加强噪声。

数学形态学边缘检测主要用到形态梯度的概念，虽也会对噪声比较敏感但不会放大噪声。

设A表示图像，B表示结构元素，⊕表示膨胀运算，表示腐蚀运算。则基本的形态梯度如下：

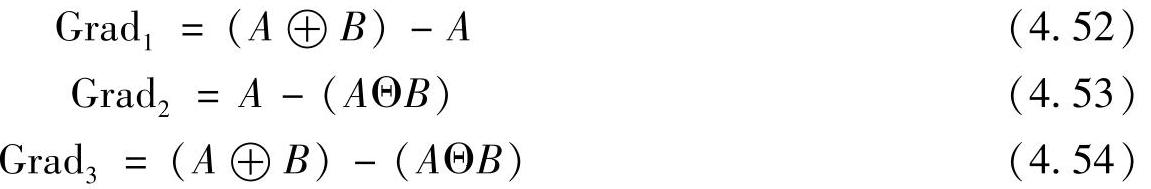
1）二值图像边缘提取 对于二值图像，膨胀运算使图像扩展，腐蚀运算使图像收缩，则上述边缘检测算子可以检测二值图像的边缘。图4.21所示为Grad₃示例。其中图4.21a为图像A，图4.21b为结构元素B，图4.21c为A⊕B，图4.21d为，图4.21e为Grad₃。即A⊕B将图像区域扩展了B/2个像素宽度，将图像区域收缩了B/2个像素宽度。这样两幅图像的差，将边缘保留下来，Grad₃给出的像素有B像素的宽度。

图4.21 Grad₃示例

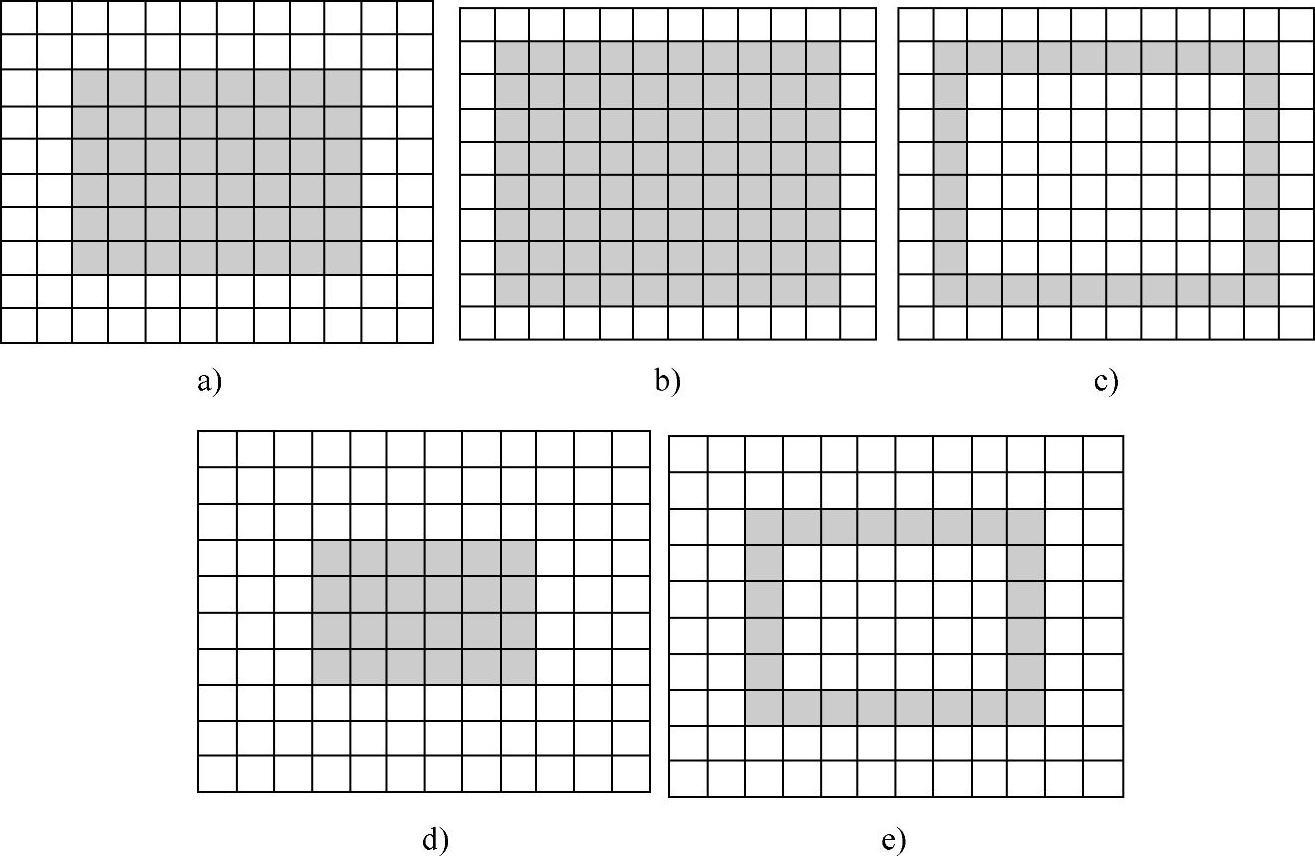
图4.22 Grad₁、Grad₂示例

较细的边界可用Grad₁、Grad₂检测。图4.22所示为Grad₁、Grad₂示例，边缘检测原理与上述Grad₃相同，Grad₁、Grad₂所给出的边界都为B/2个像素的宽度。Grad₁、Grad₂、Grad₃都没有放大噪声。采用Grad₂和3×3结构元素进行的二值图像边缘提取如图4.23所示。

2）灰度图像边缘提取 对于灰度图像，当采用一定的结构元素对图像进行膨胀运算时，图像边缘向着低灰度区扩展；当对图像进行腐蚀运算时，图像边缘向着高灰度去收缩。因此，采用上述形态梯度算子时，可以检测图像的边缘。检测到的边缘宽度与结构元素的尺度有关，设结构元素为B，Grad₁、Grad₂为B/2宽度边缘，Grad₃为B宽度边缘。图4.24详细地给出了形态梯度算子检测边缘时检测的边缘形态和结构元素尺度之间的关系。

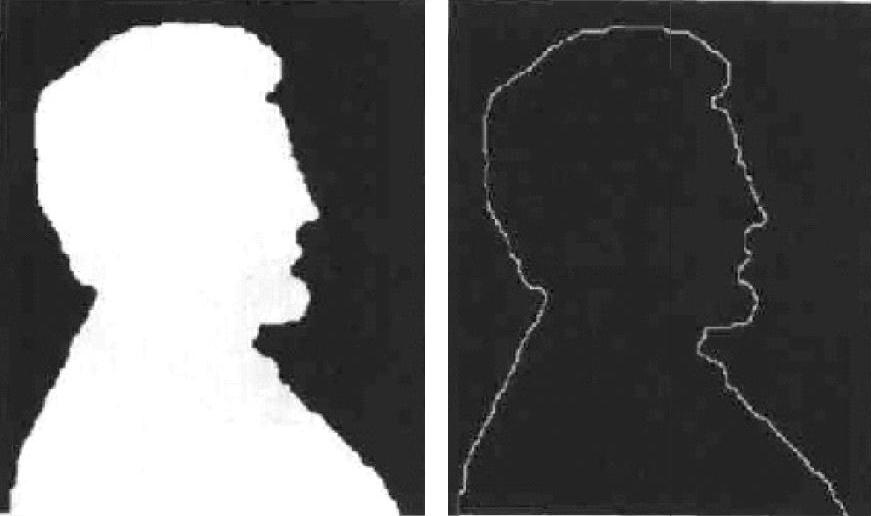
图4.23 采用Grad₂和3×3结构元素 进行的二值图像边缘提取

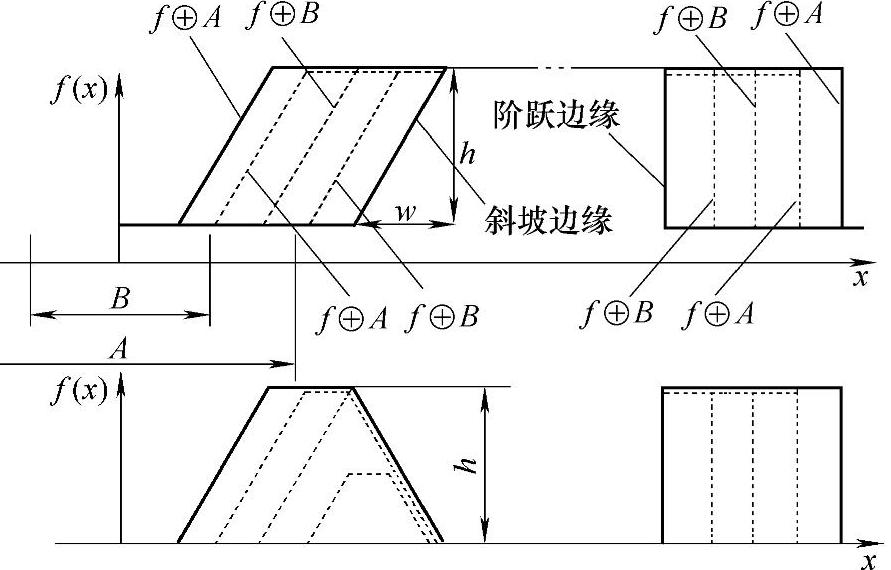
图4.24 形态梯度算子检测边缘的形态 与结构元素尺度的关系

灰度图像形态梯度算子形式与二值图像形态梯度算子相同。

（2）基于小波变换的边缘检测

设θ（t）是某一起平滑作用的低通平滑函数，且满足条件

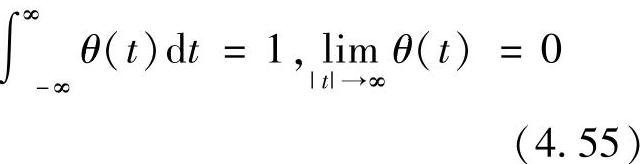
为了方便起见，不妨取θ（t）为高斯函数，即

假设θ（t）是二次可导的，并且定义ψ^（1）（t），ψ^（2）（t）分别是θ（t）的一阶和二阶导数，即

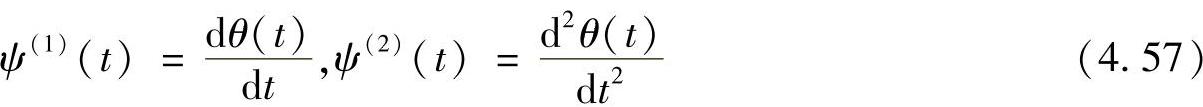
则函数ψ^（1）（t），ψ^（2）（t）满足小波函数的可容许性条件

因此，ψ^（1）（t），ψ^（2）（t）可用作小波母函数。

由于二进小波变换就是通过将原信号f（t）同伸缩小波卷积得到的，以ψ^（1）（t）为小波函数，函数f（t）在尺度为α，位置为t处的卷积型小波变换定义为

对应于ψ^（2）（t）的小波变换为

由微分是线性变换和ψ^（1）（t）和ψ^（2）（t）的定义可得

由于f*θ_α（t）是由低通平滑函数θ（t）在尺度α下对函数f（t）进行平滑的结果。由式（4.61）和式（4.62）可见，小波变换、分别是函数f（t）在尺度α下由θ（t）平滑后再取一阶与二阶导数。

若取θ（t）为三阶样条函数，如图4.25所示为ψ^（1）（t）和ψ^（2）（t）的波形。图4.26所示为函数f（t）及其在小波基ψ^（1）（t）和ψ^（2）（t）下的二进卷积型小波变换。可见：

图4.25 ψ^（1）（t）和ψ^（2）（t）的波形

1）的局部模极值点（t₀，t₁，t₂），既对应于的过零点，又对应于平滑后信号f*θ_α（t）的拐点。当α很小时，用θ（t）对f（t）平滑的结果对f（t）的突变部分的位置与形态影响不大。而当α较大时，则此平滑过程会将f（t）的一些细小突变部分消去，而只剩下大尺寸的突变。

2）当小波函数可看作某一平滑函数的一阶导数时，信号小波变换模的局部极值点对应于信号的突变点（或边缘）。当小波函数可看作某一平滑函数的二阶导数时，信号小波变换模的过零点，也对应于信号的突变点（或边缘）。

综上所述，以平滑函数的一阶导数ψ^（1）（t）为母小波作小波变换时，其小波变换在各尺度下系数的模的极大值对应信号的突变点位置。

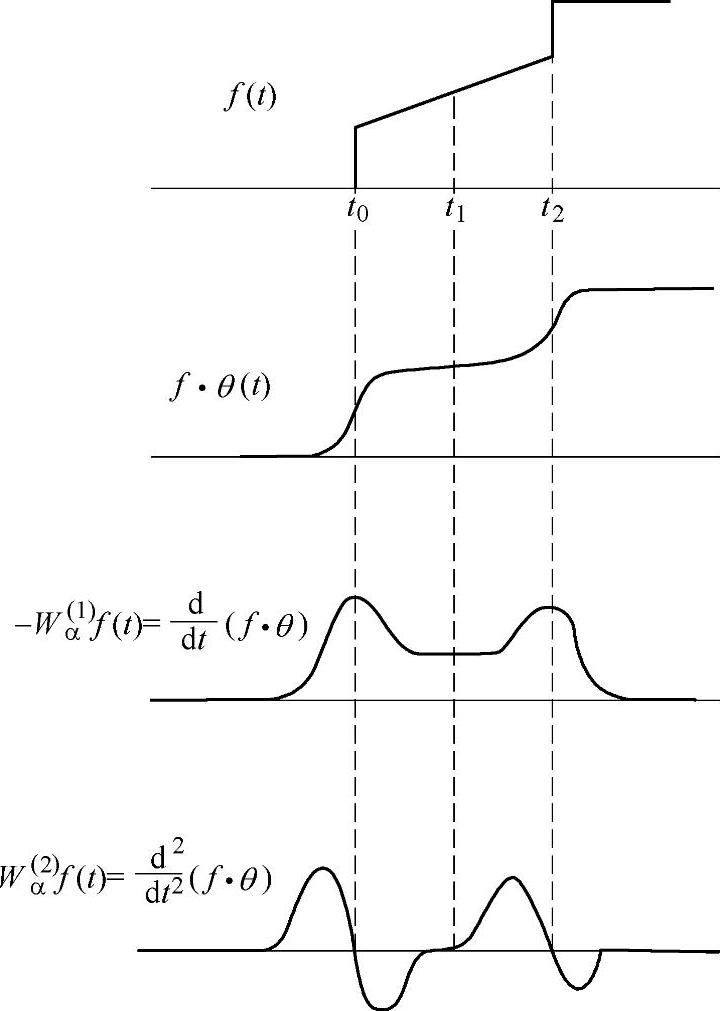
图4.26 二进卷积型小波变换

尺度α越小，θ_α（t）平滑区域小，小波系数模极大值点与突变点位置的对应就越准确。但是，小尺度下小波系数受噪声影响大，产生许多伪极值点。α大尺度下，对噪声进行了一定的平滑，极值点相对稳定。但由于平滑作用使其定位又产生了偏差，同时只有在适当尺度下，各突变点引起的小波变换才能避免交叠干扰。

因此，用小波变换模极大值法判断信号突变点时，需要把多尺度结合起来综合观察。只凭一个尺度不能定位突变点的位置。