截止频率D0的确定是理想低通滤波器设计的关键。此时，式经过修正后可以表示为3.指数低通滤波器指数低通滤波器是图像处理中常用的一种滤波器。指数低通滤波器的截止频率设计方法与巴特沃思低通滤波器基本相同。图3.12d给出了典型的梯形低通滤波器传递函数的特性曲线。图3.12 低通滤波器的特性曲线从图3.12可以看出，在D0的尾部包含一部分高频分量，因此采用梯形低通滤波器的图像清晰度比采用理想低通滤波器的图像清晰度有所改善。......
2023-11-24
频域增强与同态滤波的视觉测量技术
【摘要】：巴特沃思高通滤波具有截止频率D0的n阶巴特沃思高通滤波器的传递函数为式中，D（u，v）仍由式或式定义。图3.24 各种高通滤波器的特性曲线2.同态滤波同态滤波一种增强图像对比度的频域处理方法，尤其适合于处理由于光照不均导致的图像不清。同态滤波以式所给的图像模型为基础，在频域中同时进行图像对比度增强和压缩图像亮度范围。图3.28 同态滤波增强
频域增强通过对图像做傅里叶变换，将图像变换到频域，然后有选择地增强某些频段，再进行傅里叶反变换得到增强图像。小波域增强通过对图像做小波变换，然后增强小波分解的高频分量，再进行小波重构，即得到增强图像。流程如下：
原始图像→变换域→增强→反变换→增强图像
1.频域高通滤波锐化
频域锐化主要是通过频域高通滤波进行的。从频谱的角度看，图像模糊的实质是其高频部分被衰减，因此可以用高频滤波来使图像更加清晰。高频滤波器衰减傅里叶变换中的低频部分，而高频部分则无损地通过。与低通滤波器相对应，在高通滤波器中常用的传递函数H（u，v）有以下几种。
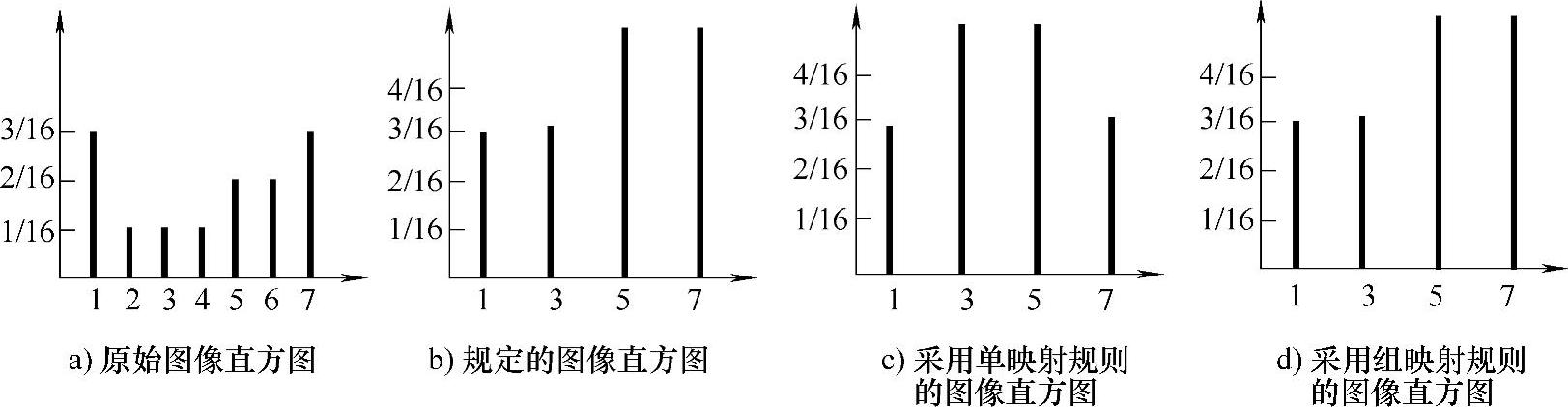
图3.23 直方图规定化计算实例
（1）理想高通滤波器（Ideal High Pass Filter，IHPF）
一个二维理想高通滤波器的传递函数H（u，v）的表达式为
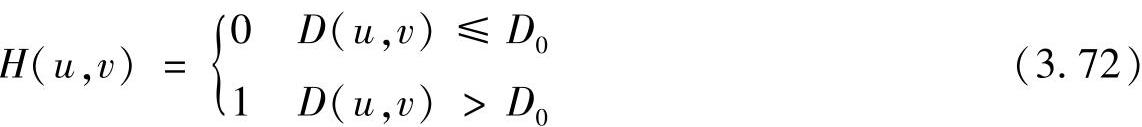
式中，D0为截止频率；D（u，v）为点（u，v）到频率平面原点的距离。理想高通滤波器传递函数的特性曲线如图3.24a所示。可见，这个滤波器与理想低通滤波器的特性正好完全相反，它把半径为D0的圆内所有频率完全衰减，对圆外的所有频率则无损通过。同理，理想高通滤波器在物理上也是不能实现的，只能用计算机进行模拟。
（2）巴特沃思高通滤波
具有截止频率D0的n阶巴特沃思高通滤波器的传递函数为
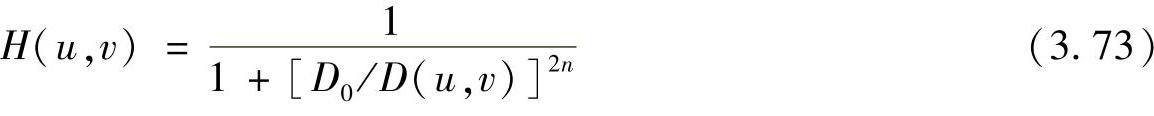
式中，D（u，v）仍由式（3.44）或式（3.45）定义。巴特沃思高通滤波器传递函数的特性曲线如图3.24b所示。
当D（u，v）=D0时，H（u，v）下降到最大值的1/2。如同巴特沃思低通滤波器的情形一样，如果截止频率的H（u，v）为最大值的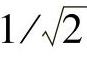
，则式（3.73）可以化简为
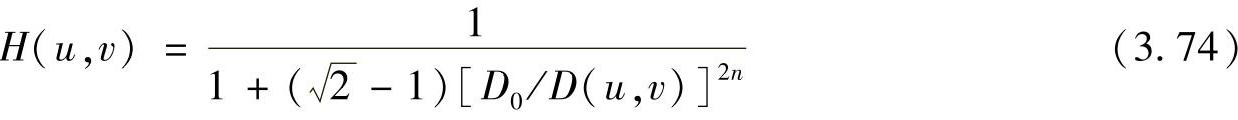
（3）指数高通滤波器（Exponent High Pass Filter，EHPF）具有截止频率D0的指数高通滤波器其传递函数表达式为
式中，D（u，v）可由式（3.44）或式（3.45）表示；n控制着指数函数的增长率。指数高通滤波器传递函数的特性曲线如图3.24c所示。
当D（u，v）=D0时，H（u，v）下降到最大值的1/2。如同指数低通滤波器的情形一样，如果截止频率的H（u，v）为最大值的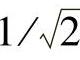
，则式（3.75）可以化简为
（4）梯形滤波器（Trapezia High Pass Filter，THPF）梯形高通滤波器的传递函数表达式为
式中，D（u，v）仍由式（3.44）或式（3.45）定义；D0为截止频率。图3.24d所示为典型的梯形高通滤波器传递函数的特性曲线。
图3.24 各种高通滤波器的特性曲线
2.同态滤波
同态滤波一种增强图像对比度的频域处理方法，尤其适合于处理由于光照不均导致的图像不清。它与图像成像模型有密切关系。因此在介绍同态滤波之前，先简单介绍一下图像的成像原理。
人之所以能够看到某个物体，是因为有光照射在物体上，物体将入射光沿着一定方向进行反射或透射。反射/透射光进入人眼后在视网膜上产生感知信号。该感知信号沿着视神经传送到大脑后形成物体的像。按照图像的成像原理，可以将图像函数f（x，y）分为两部分：入射到可见场景上的光i（x，y）和场景中物体对入射光的反射/透视。前者也称为照度分量、照射分量，后者用反射率或透射率r（x，y）表示，也称为反射分量。因此可以将一幅图像进行如下简单建模：(www.chuimin.cn)
式中，i（x，y）的值由光源决定；反射率r（x，y）由场景中的物体的属性决定，取值范围在全吸收（0）和全反射（1）之间。
在一幅图像中，反射分量决定图像的内容，随图像细节的不同在空间上作快速变化。而照度分量在空间则通常具有缓慢变化的性质。所以照度分量的频谱分布在低频区域，而反射分量的频谱则大部分分布在空间的高频区域。为了增强图像的细节表现，必须改善照度分量和反射分量的分布。
同态滤波以式（3.78）所给的图像模型为基础，在频域中同时进行图像对比度增强和压缩图像亮度范围。其基本思想是，将图像模型的两个分量分开，在频域中选择适当的滤波器参数H（u，v），在抑制图像低频信号i（x，y）的同时加强其高频信息r（x，y）。最后将频域信号反变换到空间域即可得到预期的效果。
为了把照度分量和反射分量分开处理，一种方法就是对式（3.78）进行对数变换，这样就可以把两者混合在一起的乘法运算转变成两者分离的加法运算。然后在频域中抑制低频照度分量并加强反射分量，最后再将处理结果反变换到空间域中，从而得到预期的效果。同态滤波的基本流程如图3.26所示。
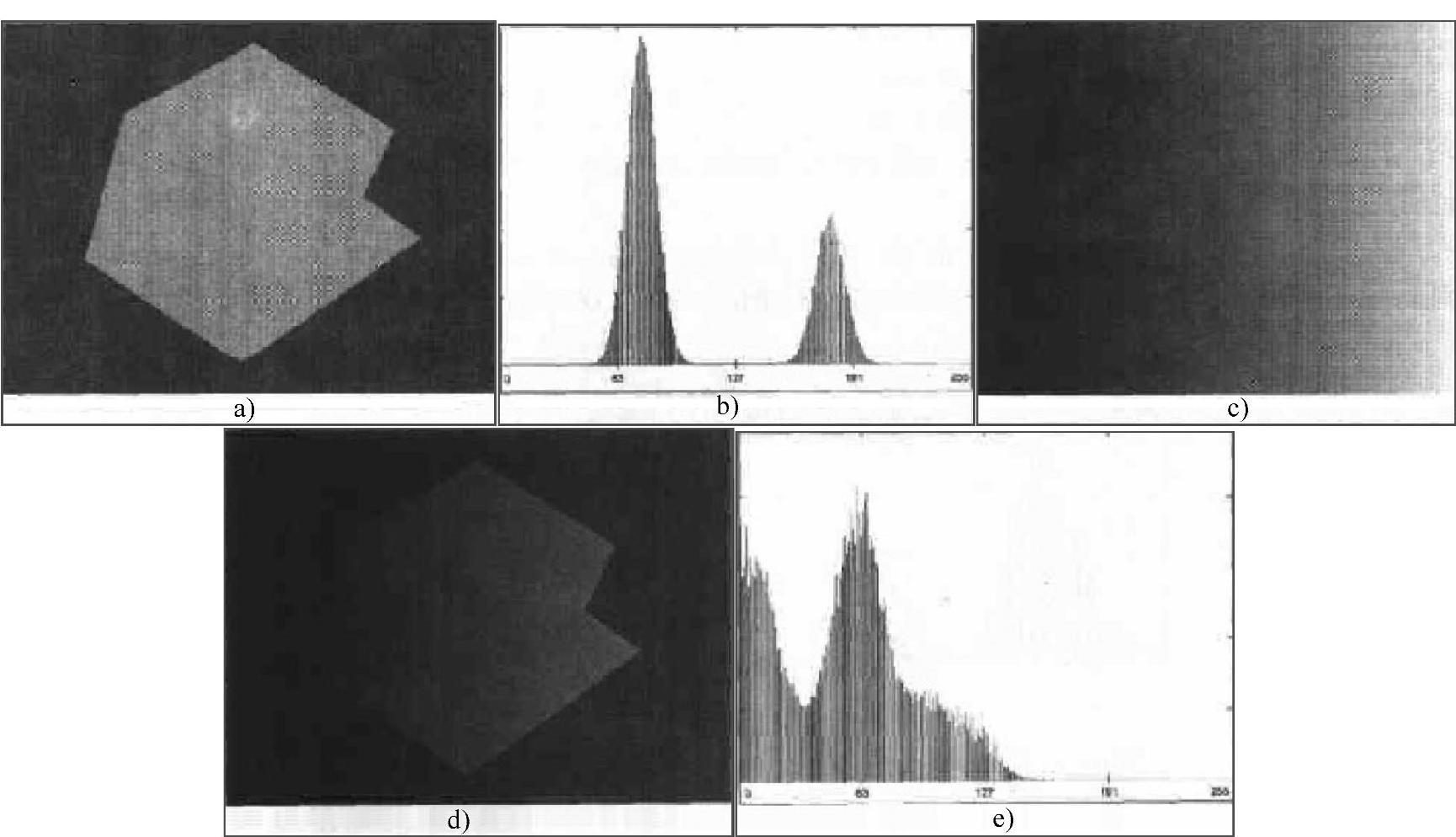
图3.25 图像模型示意图
图3.26 同态滤波的流程
1）首先对式（3.78）的成像模型两边取对数，即
lnf（x，y）=lni（x，y）+lnr（x，y） （3.79）
2）对式（3.79）进行正向傅里叶变换，即
F（u，v）=I（u，v）+R（u，v） （3.80）
3）选择一个适当的频域函数H（u，v）进行滤波，即
H（u，v）F（u，v）=H（u，v）I（u，v）+H（u，v）R（u，v） （3.81）
4）根据需要对滤波后的数据进行处理。
5）将处理后的频域结果经过傅里叶反变换转换到对数空间域里，则有
hf（x，y）=hi（x，y）+hr（x，y） （3.82）
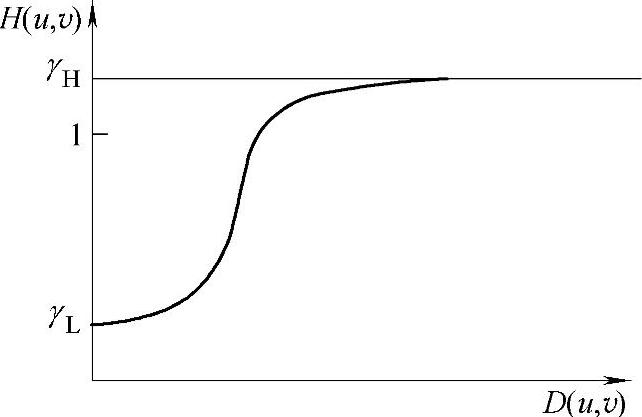
图3.27 同态滤波器圆对称滤波函数的剖面图，D（u，v）表示点（u，v）离原点的距离
6）将式（3.82）进行指数变换，得到数字图像所在的空间，即
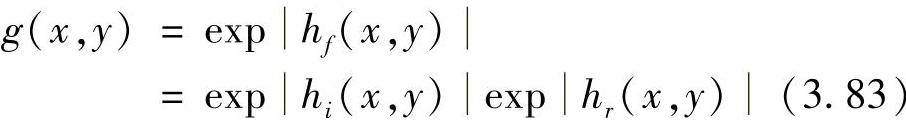
可见，H（u，v）的选择决定了同态滤波的效果。为了能够在抑制低频的同时加强高频信息，H（u，v）通常在低频部分小于1，而在高频部分大于1。图3.27给出了一个满足上述要求的滤波函数剖面图，将它绕纵轴旋转360°即得到完整的二维H（u，v）。
【例3.10】 用同态滤波增强
在图3.28a所示的原始图像中，掩体内部的细节被遮蔽。图3.28b所示为用同态滤波器处理的结果，其中滤波函数γL=0.5，γH=2.0，减小了亮度的动态范围，增强了对比度可以使掩体内的细节显示出来，并且平衡墙外的灰度。增强后的图像更加锐化。
图3.28 同态滤波增强
有关视觉测量技术的文章
- 详细阅读
-
频域滤波的基本步骤及应用-视觉测量技术详细阅读
空间域和频域之间最基本的联系是卷积计算。3）在频域中，计算滤波器函数H（u，v）和F（u，v）的点积G（u，v）。 二维离散傅里叶变换实例图3.10a所示为在尺寸为512×152像的黑色背景上叠加一个尺寸为20×40的白色矩形。......
2023-11-24
- 详细阅读
-
视觉测量技术-空间域增强的映射函数设计详细阅读
空间域增强的关键在于设计一个合适的映射函数。分段线性灰度变换图3.13 线性灰度变换的映射函数示意图图3.14 三段线性灰度变换的映射函数示意图分段线性灰度变换将整个图像灰度空间分成两段甚至多段，每段分别作线性变换，且斜率不同。......
2023-11-24
-
视觉测量技术的研究目标详细阅读
借鉴人类视觉的原理，计算机视觉技术研究的长远目标是建立通用的视觉系统。计算机视觉技术的优势不仅在于能模拟人眼的功能，还能完成人眼所不能胜任的工作。因此，对人脑视觉的充分理解将促进对计算机视觉更深入的研究，并对计算机视觉系统提供坚实的生物理论基础。......
2023-11-24
-
视觉测量技术：计算机视觉测量方案详细阅读
计算机视觉测量技术以图像传感器为手段检测空间物体的空间三维坐标，进而检测物体的尺寸、形状和运动状态等。美国、加拿大、日本等发达国家早在20世纪60年代后期就已经开始了计算机视觉测量技术的研究。直到20世纪90年代，随着计算机技术的发展成熟，计算机视觉测量技术逐渐成为一个研究热点。......
2023-11-24
-
摄像机模型与视觉测量技术详细阅读
图5.11 世界坐标系与摄像机坐标系不重 合时的投影成像2.世界坐标系与摄像机坐标分开时的摄像机模型考虑更一般的情况，即摄像机坐标系和世界坐标系分开的情况，但仍将平面xy和像平面x′y′重合。图5.11所示为这种情况下的摄像机几何模型，像平面中心（原点）与世界坐标系的位置偏差记为矢量D，其分量为Dx、Dy、Dz。图5.12所示为考虑这些因素时的通用摄像机模型示意图。......
2023-11-24
-
Marr视觉理论简介：视觉测量技术详细阅读
下面简要介绍Marr视觉理论的基本思想和框架。图1.1 Marr视觉信息处理的三个阶段第一阶段是早期视觉处理，其目的是从输入的原始图像中抽取观察者周围景物表面的物理特性，如距离、表面方向、材料特性等，并构成要素图或基元图。表1.2 由图像恢复形状信息的表达框架3.Marr视觉理论的意义及不足Marr视觉理论是计算机视觉研究领域的划时代成就。图1.2 改进后的Marr视觉理论框架限于历史等因素，Marr没有研究如何用数学方法严格地描述视觉信息的问题。......
2023-11-24
相关推荐