直方图均衡化方法的优点是能自动增强整个图像的对比度,处理的结果是得到全局均衡化的直方图。这种增强的方法称为直方图规定化方法。直方图规定化方法的基本原理与直方图均衡化方法非常类似,两者的不同主要在于变换函数的选取上。在实际应用中,直方图规定化方法的难点也恰恰在于如何恰当地选取有意义的特定直方图。可见,单映射规则的映射方向是将原始累积直方图中的各项映射成规定的累积直方图的各项。 直方图规定化计算示例。......
2023-11-24
1.直方图
直方图是数字图像处理中的一个重要概念。所谓直方图是关于图像中灰度分布的函数,即将数字图像中的所有像素,按照灰度值的大小,统计每个灰度值的概率。对于数字图像所出现的概率值,其表达式为
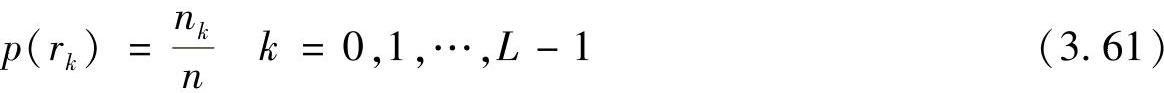
式中,rk为图像f(x,y)的第k级灰度值;nk为f(x,y)中具有灰度值rk的像素的个数;n为图像像素总数;L为灰度等级数,最常用的灰度等级数是256。
可见直方图提供了一幅图像所有灰度值的整体分布描述。通常直方图用二维图形表示,横坐标表示图像的灰度级,纵坐标代表每个灰度级的像素数占全图部像素数的百分比。这样,通过灰度直方图就可以对图像的某些整体特性进行描述。
图3.17所示为四个基本图像(亮、暗、低对比度与高对比度)及其对应的灰度直方图。从图中可以看出,暗图像由于拥有较多的低灰度值像素,因此它的直方图主要分布在低灰度区,而高灰度区的灰度分布函数值较小或为0;亮图像则拥有较多灰度值较高的像素,其直方图分布主要集中在高灰度区,低灰度区的灰度分布函数值较小或为0;低对比度的图像的直方图则主要集中在某个灰度区域内,其他区域内的像素数则较少;而高对比度的图像的直方图分布比较均匀,基本覆盖了所有的像素灰度级。
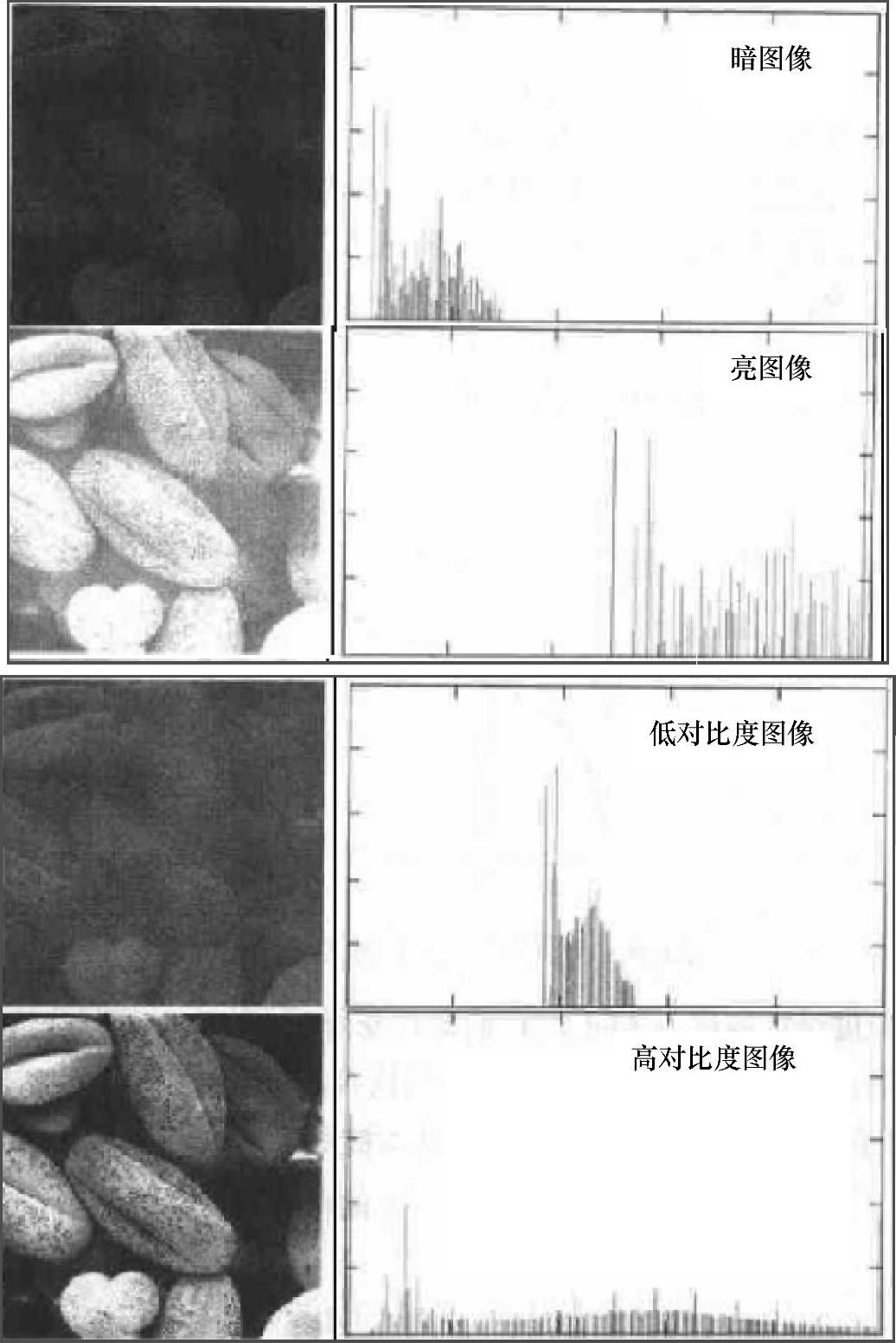
图3.17 四个基本图像(亮、暗、低对比度、高对比度图像)及其对应的灰度直方图
总之,图像的直方图包含了非常丰富的信息,是图像处理中的一种十分重要的分析工具。它具有如下三条性质:
1)直方图是一幅图像中各像素灰度出现频次的统计结果,它只反映图像中不同灰度值出现的次数,而不反映某一灰度所在的位置。也就是说,它只包含了该图像的某一灰度像素出现的概率,而忽略其所在的位置信息。
2)任意一幅图像,都有惟一确定的一幅直方图与之对应。但不同的图像可能有相同的直方图,即图像与直方图之间是多对一的映射关系。
3)由于直方图是对具有相同灰度值的像素进行统计而得到的,因此一幅图像中各部分区域的直方图之和等于整个图像的直方图。
直方图变换的关键也是寻找一个恰当的变换函数T(r),通过调整图像的直方图而达到调整图像对比度的目的。常用的直方图变换方法有直方图均衡化方法与直方图规定化方法。
2.直方图均衡化方法
直方图均衡化方法的基本思想是把原始的直方图变换成均匀分布的形式。增加了像素灰度值的动态范围,达到增强图像整体对比度的效果。
(1)灰度级及变换函数
假设变量r表示待增强图像的灰度级,r在[0,L-1]。为讨论问题方便,将r归一化到区间[0,1],且r=0表示黑色及r=1表示白色。考虑一个连续函数T(r),对任意一个满足上述条件的r,进行如下变换:
s=T(r),0≤r≤1 (3.62)即对于每一个像素值r产生一个相应的灰度值s。上述变换函数T(r)需满足如下条件:A,T(r)在0≤r≤1中为单值且单调递增;B,当0≤r≤1时,0≤T(r)≤1。条件A要求T(r)为单值是为了保证反变换存在,单调条件则保持输出图像从黑到白顺序增加。变换函数不单调增加将导致至少有一部分亮度范围被颠倒,从而在输出图像中产生一些反转灰度级。条件B保证输出灰度级与输入有同样的范围。由s到r的反变换可以表示为
r=T-1(s),0≤s≤1 (3.63)
(2)概率密度函数的关系
图像灰度级可以看作[0,1]区间的随机变量。随机变量可以采用概率密度函数(Proba-bility Density Function,PDF)描述。令Pr(r)和Ps(s)分别代表随机变量r和s的概率密度函数。
由概率理论可知,如果Pr(r)和T(r)已知,且T-1(s)满足条件B,那么由T(r)变换后的随机变量s的概率密度函数Ps(s)为

即随机变量s的概率密度函数由输入图像的灰度级PDF和所选择的变换函数决定。
(3)累积分布函数
选择累积分布函数作为变换函数,即

式中,w为积分变量。式(3.65)为随机变量r的累积分布函数(Cumulative Distribution Func-tion,CDF)。累积分布函数的具有如下特点:①概率密度函数永远为正,函数积分是一个函数曲线下的面积,所以累积分布函数是单值单调增加,满足变换函数条件A;②区间[0,1]上变量的概率密度函数的积分也在区间[0,1]上,因此满足变换函数条件B。
因此,累积分布函数满足变换函数的条件,可以作为图像灰度变换的变换函数。
(4)Ps(s)分布
原图像灰度级变量r通过变换函数T(r),得到变换后的灰度级变量s,其概率密度函数为Ps(s)。由微积分原理,关于上限的定积分的导数就是该上限的积分值,即

将此结果代入式(3.64),取概率值为正,得到
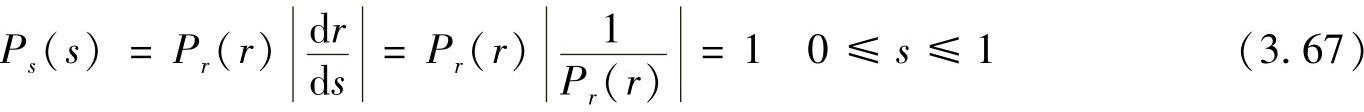
(5)结论
因为Ps(s)是概率密度函数,所有s值上的积分等于1。区间[0,1]以外其值为0,式(3.67)中给出的Ps(s)形式为均匀概率密度函数。
可见,按照式(3.65)给出的变换函数得到一个随机变量s,其概率密度函数为均匀分布,与Pr(r)的形式无关。均匀分布表明,图像的直方图是均匀的,图像对比度得到了增强。
(6)离散图像操作
对于离散值,处理其概率与和,而不是概率密度函数与积分。一幅图像中灰度级rk出现的概率近似为
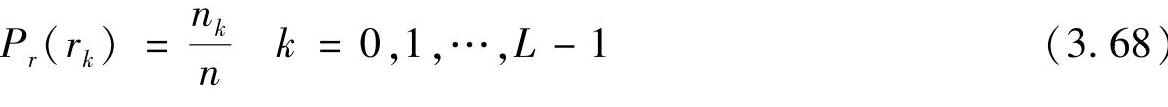
式中,n为图像中像素的总和;nk为灰度级为rk的像素的个数;L为图像中可能的灰度级总数。式(3.65)中变换函数的离散形式为
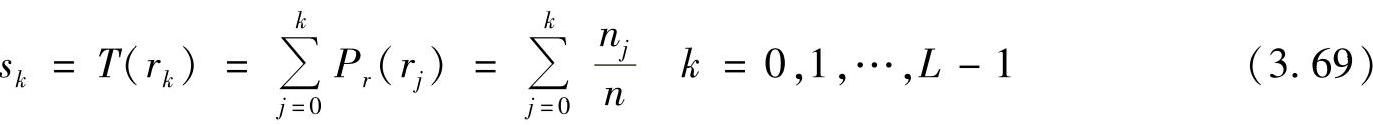
通过式(3.69),将输入图像中灰度级为rk的各像素映射到输出图像中灰度级为sk的对应像素。
(7)直方图均衡化计算步骤
综上所述,直方图均衡化图像增强方法的实现步骤如下:
1)列出原始图像灰度级rk,k=0,1,…,L-1;
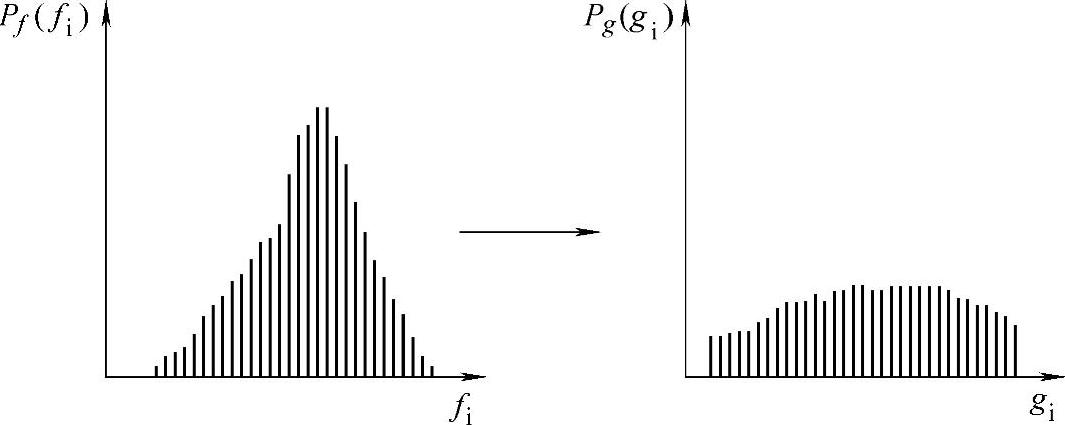
图3.18 直方图均衡化示意图
2)统计原始直方图各灰度级像素nk;
3)用式Pr(rk)=nk/n,k=0,1,…,L-1,0≤rk≤1计算原始直方图;
4)计算累积分布函数,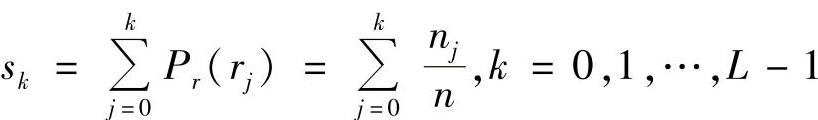 ;
;
5)由于上面计算的sk取值范围为0~1,而数字图像的灰度范围为[0,L-1],因此需将归一化的灰度值恢复到数字图像原来的灰度范围。即进行取整操作,sk=int[(L-1)sk+0.5](四舍五入);
6)确定映射对应关系(rk→sk);
7)统计新直方图各灰度级像素nk;(www.chuimin.cn)
8)用Ps(sk)=nk/n计算新直方图。
如前所述,式(3.69)~式(3.75)给出的变换或映射称为直方图均衡化。直方图均衡化可以展开图像的直方图,使图像灰度级能跨越更大的范围。
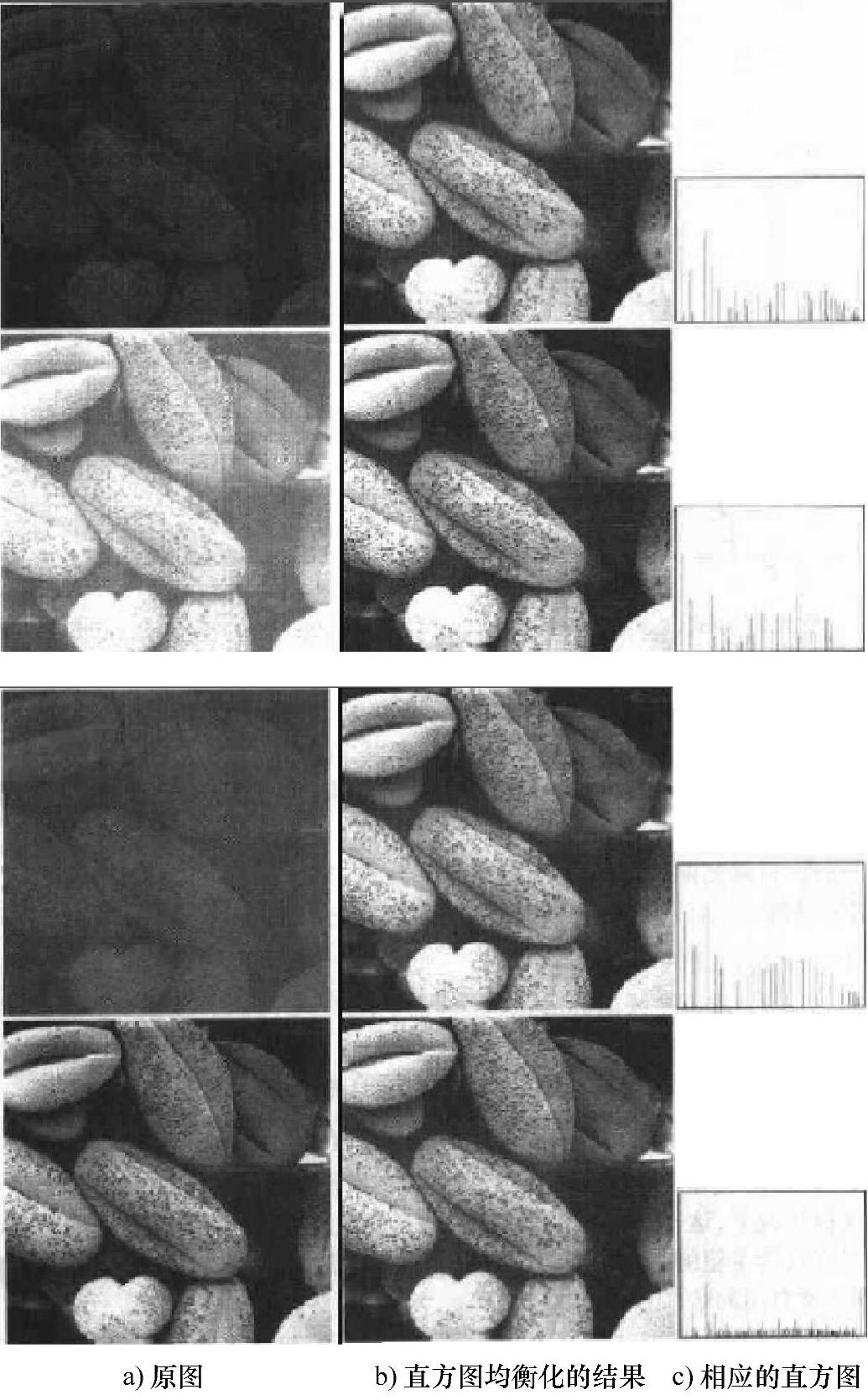
图3.19 直方图均衡化
图3.19a所示为四幅图像,图3.19b所示是对这些图像进行直方图均衡化的结果。前三种结果显示了明显的改进效果。第四幅图像在视觉效果上没有明显改变,这是因为原图像的直方图本来就是比较均匀的。对于不同的原始图像,直方图均衡化后的视觉效果很相似,说明直方图均衡化是适应性较强的增强工具。
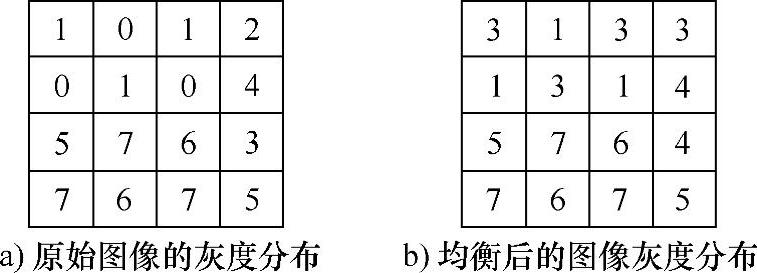
图3.20 直方图均衡实例图像的灰度
【例3.7】 直方图均衡化计算。
以图3.20a给出的大小为4×4、灰度等级为8的图像来分析直方图均衡化方法的使用。
(1)列出图像的各个灰度级
0,1,2,3,4,5,6,7
(2)统计每个灰度级的像素个数
n0=3,n1=3,n2=1,n3=1,n4=1,n5=2,n6=2,n7=3
(3)计算直方图中的各项
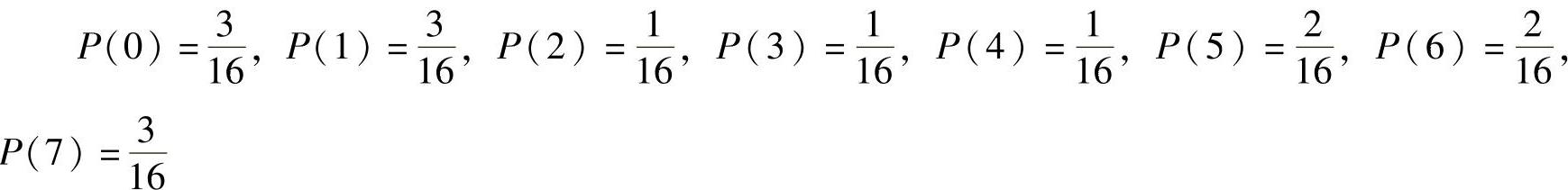
(4)计算直方图的累积分布函数

(5)计算灰度均衡后的离散灰度值
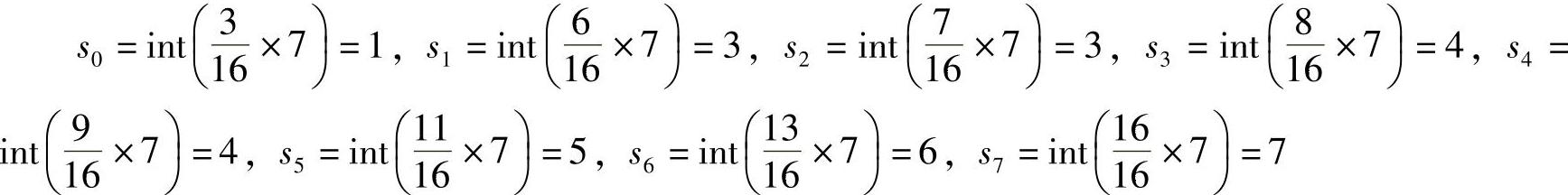
可见,经过直方图均衡化后,仅需要1、3、4、5、6、7共6个灰度级。修正后每个灰度级对应的像素数和概率值也均已经发生了变化。其中,修正后图像各个灰度级的像素数分别为3、4、2、2、2和3。
均衡化后的直方图如图3.21b所示。原图直方图的灰度级主要集中在低灰度级和高灰度级。在均衡化后的图像中,中灰度级也得到了一定扩展。整个直方图显得比较均匀,但并非完全均匀,且灰度间隔被拉大。
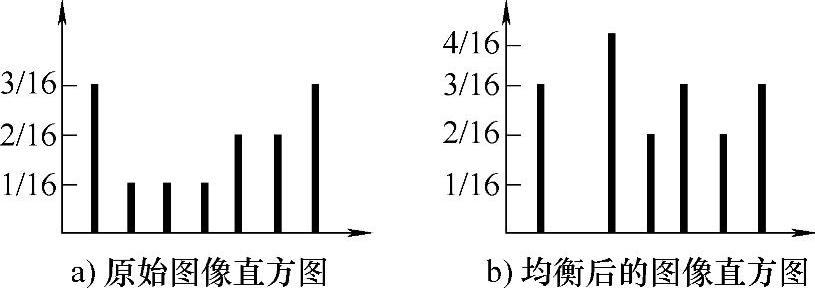
图3.21 直方图均衡化示例
从理论上讲,直方图灰度均衡就是通过变换函数将原图的直方图调整为均匀的直方图。而实际上修正后的直方图并不是十分均衡,因为原图像中某些像素数比较少的灰度级可能会和与之相邻的像素数较多的灰度级归并到同一个灰度级上,从而造成灰度间隔的扩大。此外,由于不能将同一个灰度值的各个像素变换到不同灰度级,也导致直方图均衡化只能是近似均衡直方图,不能实现理想的水平直线均衡结果,并且致使某些图像细节消失。
【例3.8】 直方图均衡化计算
以一幅64×64像素,8个灰度等级的图像为例,进行直方图均衡化计算,其各灰度级的概率分布见表3.1。具体计算过程如下:
表3.1 各灰度级对应的概率分布

第一步,根据表3.1中的数据得到原始图像的直方图,如图3.22a所示。利用式(3.69)得到变换函数的值为
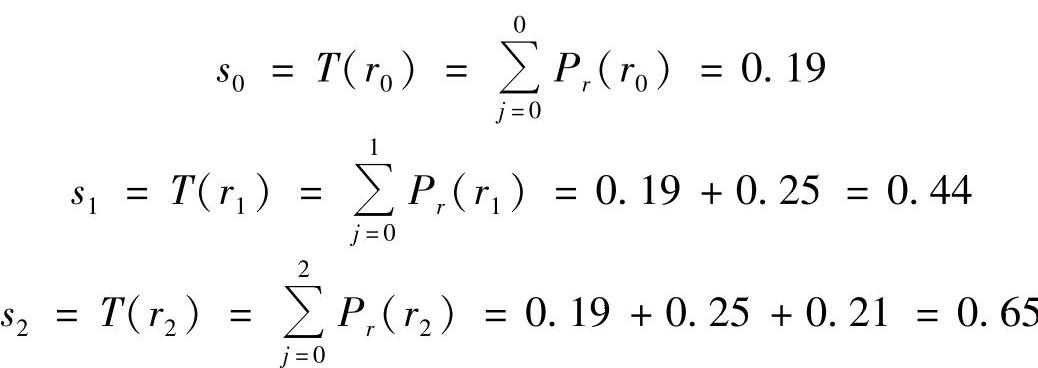
依次类推,可得到
s3=0.81,s4=0.89,s5=0.95,s6=0.98,s7=1.0
这样变换函数T(rk)与灰度级sk之间的关系曲线如图3.22b所示。
第二步,采用公式sk=int[(L-1)sk+0.5],将sk扩展到[0,L-1]范围内并取整,可得
s0=1,s1=3,s2=5,s3=6,s4=6,s5=7,s6=7,s7=7
然后将相同的值归并起来,即可得到直方图均衡化修正后的灰度级,依次为
s'0=1,s'1=3,s'2=5,s'3=6,s'4=7
由此可知,经过变换后的灰度级不需要8个,只需5个就够了。把相应的原灰度级像素数相加即可得到新灰度级的像素数,统计新直方图各灰度级像素为
n'0=790,n'1=1023,n'2=850,n'3=985,n'4=448
第三步,确定rk→sk的映射
r0→s'0→790
r1→s'1→1023
r2→s'2→850
r3,r4→s'3→656+329=985
r5,r6,r7→s'4→245+122+81=448
第四步,新灰度级分布
Ps(s0)=790/4096=0.19,Ps(s1)=1023/4096=0.25,
Ps(s2)=850/4096=0.21,Ps(S3)=985/4096=0.24,
Ps(S4)=448/4096=0.11
第五步,均衡化后的直方图如图3.22c所示。
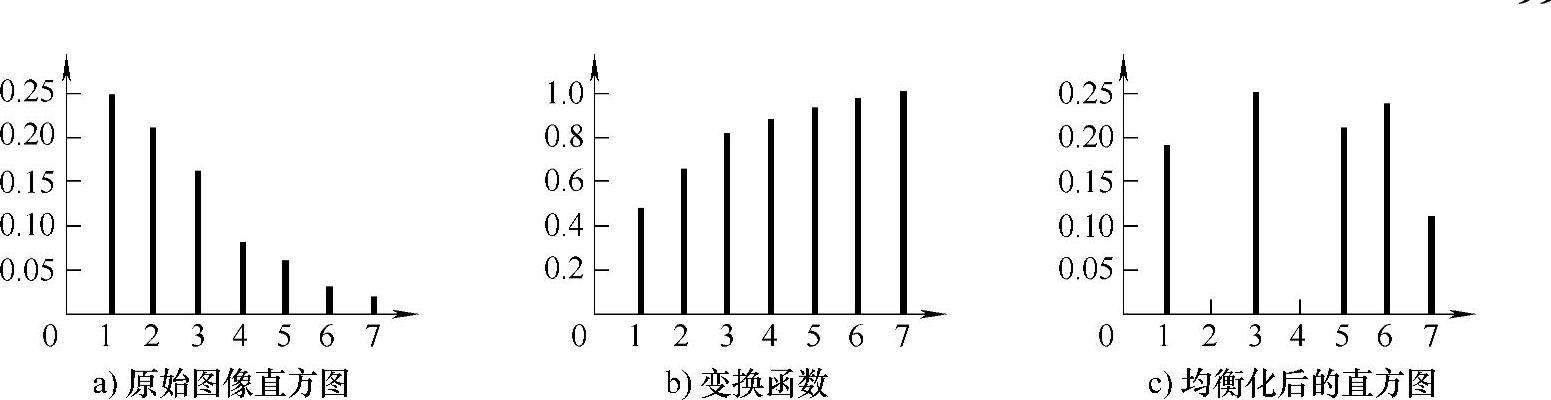
图3.22 直方图均衡化示例
有关视觉测量技术的文章

直方图均衡化方法的优点是能自动增强整个图像的对比度,处理的结果是得到全局均衡化的直方图。这种增强的方法称为直方图规定化方法。直方图规定化方法的基本原理与直方图均衡化方法非常类似,两者的不同主要在于变换函数的选取上。在实际应用中,直方图规定化方法的难点也恰恰在于如何恰当地选取有意义的特定直方图。可见,单映射规则的映射方向是将原始累积直方图中的各项映射成规定的累积直方图的各项。 直方图规定化计算示例。......
2023-11-24

直方图变换法的基本思想是,利用像素邻域的局部性质变换原始直方图为新的直方图。这个新直方图与原直方图相比,或者峰之间的谷变深了;或者谷转变为峰,更容易检测了。图4.40b给出了图像中一段边缘的剖面,这段剖面可分为Ⅰ、Ⅱ、Ⅲ三个部分。梯度直方图如图4.40c所示,梯度直方图有两个峰,分别对应目标与背景的内部区和过渡区。图4.40 边缘及梯度直方图根据上述讨论,可将图像的直方图进行变换,加大直方图中峰谷之间的距离。......
2023-11-24

单目视觉测量是指利用一台摄像机或数码相机拍摄图像进行测量工作。但由于标定精度弱和难以同时确定摄像机与被测物体之间的相对位置等问题,单目视觉的整体测量精度不如双目和多目视觉测量系统。单目视觉测量的理论基础和相关技术是双目测量乃至多目测量技术的基础。单目视觉测量能够满足某些应用场合实际测量的要求。基于单目视觉的测量方法主要包括几何相似法、光笔式三坐标测量法、几何形状约束法、几何光学法和结构光测量等。......
2023-11-24

成像系统的几何畸变误差是典型的系统误差,是影响光学测量精度的因素之一。选用高质量的镜头和进行镜头畸变校正可提高测量精度。......
2023-11-24

借鉴人类视觉的原理,计算机视觉技术研究的长远目标是建立通用的视觉系统。计算机视觉技术的优势不仅在于能模拟人眼的功能,还能完成人眼所不能胜任的工作。因此,对人脑视觉的充分理解将促进对计算机视觉更深入的研究,并对计算机视觉系统提供坚实的生物理论基础。......
2023-11-24

图4.10 边缘模型边缘检测是基于边界分割方法的最基本处理。实际边缘模型是如图4.10b所示的水平剖面图,称为斜坡边缘。斜坡部分与边缘的模糊程度成比例。阶跃型边缘处于图像中两个具有不同灰度值的相邻区域之间,其灰度变化曲线的一阶导数在边缘处出现极值,而二阶导数在边缘处出现零交叉。脉冲型边缘主要对应于细条状的灰度值突变区域。边缘检测包含两个方面含义:1)检测边缘点或边缘线段。......
2023-11-24

计算机视觉测量技术以图像传感器为手段检测空间物体的空间三维坐标,进而检测物体的尺寸、形状和运动状态等。美国、加拿大、日本等发达国家早在20世纪60年代后期就已经开始了计算机视觉测量技术的研究。直到20世纪90年代,随着计算机技术的发展成熟,计算机视觉测量技术逐渐成为一个研究热点。......
2023-11-24
相关推荐