线性空间域滤波借助模板与图像进行卷积并在邻域操作。图3.5a所示为一个3×3的均值滤波器，将其应用于图3.4a的子图像，其滤波结果为对于与图3.3b所示模板对应的像素区域，采用图3.5a所示的滤波器进行滤波，其结果为均值滤波器减小了图像灰度的“尖锐”变化。非线性空间域滤波器能够较好地处理椒盐噪声、脉冲噪声和孤立噪声点。 中值滤波器的使用图3.6所示是利用3×3的模板进行中值滤波的示例。......
2023-11-24
视觉测量技术-空间域增强的映射函数设计
【摘要】：空间域增强的关键在于设计一个合适的映射函数。分段线性灰度变换图3.13 线性灰度变换的映射函数示意图图3.14 三段线性灰度变换的映射函数示意图分段线性灰度变换将整个图像灰度空间分成两段甚至多段，每段分别作线性变换，且斜率不同。
1.灰度变换基本原理
空间域增强是在图像空间直接对图像的灰度值进行处理，并使处理后的图像清晰度增加，因此也称为灰度变换方法。灰度变换主要包括直接灰度变换和直方图变换两大类方法。
灰度变换的基本原理可以描述为，设r和s分别代表原始图像f（x，y）和增强图像g（x，y）的灰度，T（）为映射函数，通过映射函数T（）将f（x，y）中的灰度r映射成g（x，y）中的灰度s，使得图像灰度的动态范围得以扩展或压缩，从而改善图像的对比度。空间域增强的关键在于设计一个合适的映射函数。目前，映射函数的设计主要有如下两类方法：
1）根据图像特点和处理工作需求，人为设计映射函数，试探其处理效果。
2）从改变图像整体的灰度分布出发，设计一种映射函数，使变换后图像灰度直方图达到或接近预定的形状。映射变换的类型取决于所需增强特性的选择。
2.直接灰度变换
直接灰度变换是图像对比度增强的一种有效手段。其特点是变换过程与图像的像素位置及被处理像素的邻域灰度无关，是一种典型的基于像素的空间域处理方法。直接灰度变换主要有三种方法：线性灰度变换、分段线性灰度变换和非线性灰度变换。
（1）线性灰度变换
顾名思义，线性灰度变换的映射函数为线性函数（见图3.13），其表达式为
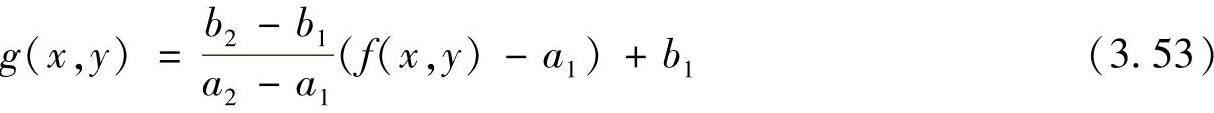
式中，a1与a2可从直方图上获得。显然，若|b1-b2|＞|a1-a2|，则图像的对比度被扩展。对离散图像而言，变换前后的图像像素总数尽管不变，但不同像素之间的灰度差加大，因此对比度加大，图像质量得以提高。线性灰度变换的特点是，对整个图像的灰度一视同仁，均按同一个规律进行拉伸处理。
（2）分段线性灰度变换
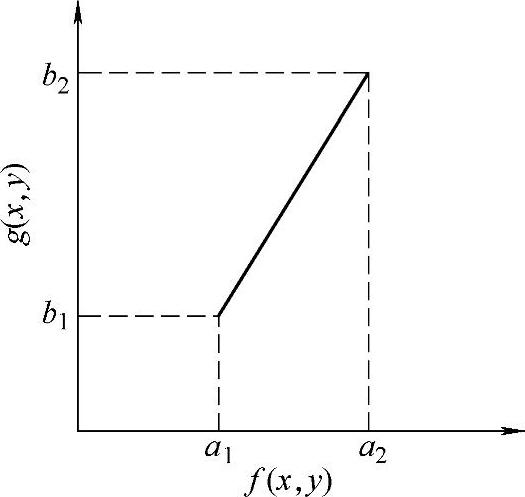
图3.13 线性灰度变换的映射函数示意图
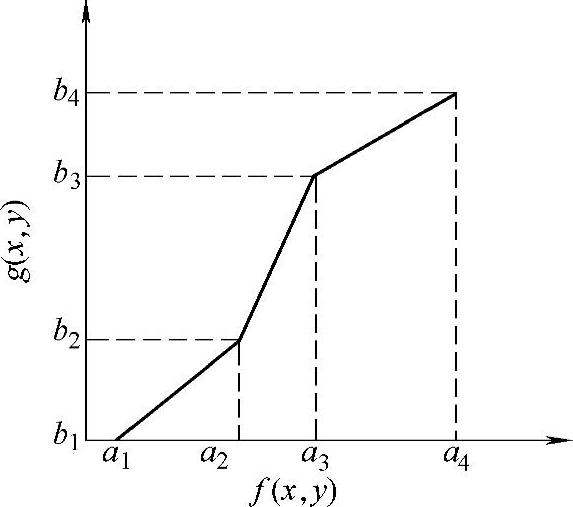
图3.14 三段线性灰度变换的映射函数示意图
分段线性灰度变换将整个图像灰度空间分成两段甚至多段，每段分别作线性变换，且斜率不同。分段线性变换的优点是可以根据用户的需要，拉伸感兴趣的图像灰度细节，相对地抑制不感兴趣的灰度级。图3.14所示为一个分三段作线性灰度变换的函数，其数学表达式为
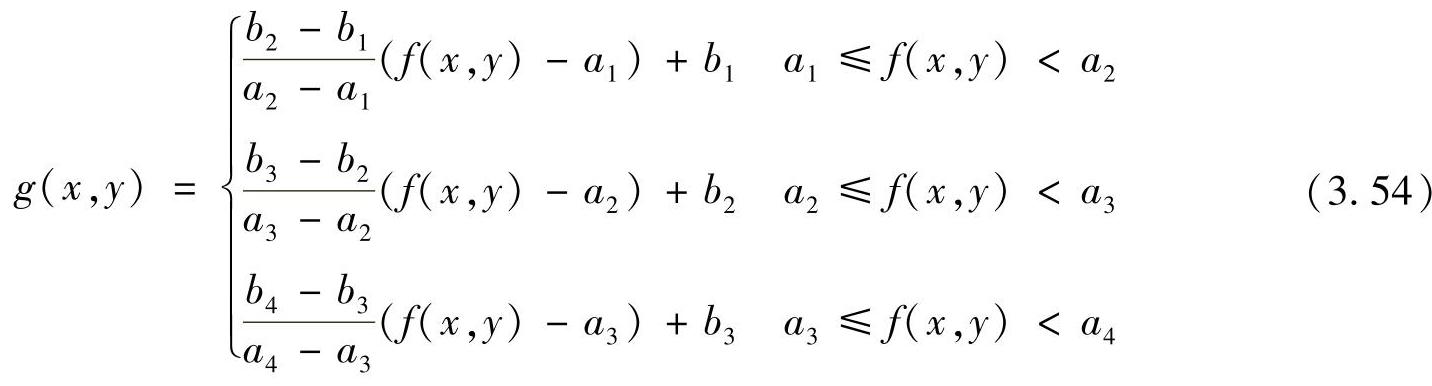
式中，a1，a2，a3，a4和b1，b2，b3，b4分别是线段l1，l2，l3的端点坐标。
如果|b1-b2|＞|a1-a2|、|b3-b2|＜|a3-a2|和|b4-b3|＜|a4-a3|，则扩展第一区间[a1，a2]的灰度值，压缩第二区间[a2，a3]与第三区间[a3，a4]的灰度值，因此得到低灰度级被增强的图像。
如果|b1-b2|＜|a1-a2|，|b3-b2|＞|a3-a2|，|b4-b3|＜|a4-a3|，则扩展第二区间[a2，a3]的灰度值，压缩第一区间[a1，a2]与第三区间[a3，a4]的灰度值，因此得到中灰度级被增强的图像。
如果|b4-b3|＞|a4-a3|，且|b1-b2|＜|a1-a2|、|b3-b2|＜|a3-a2|，则图像的高灰度级被增强。
图3.15所示为四种典型的分段线性灰度变换函数。其中，两端裁剪的分段线性灰度变换用于扩展中间灰度区，而将低灰度区和高灰度区强行压缩为固定的值；锯齿形变换用于显现图像的轮廓线，它能把不同灰度范围变换成相同的灰度范围输出；反转变换主要用于图像的反转，并裁剪高亮区部分；裁剪变换则用于图像的二值化。(www.chuimin.cn)
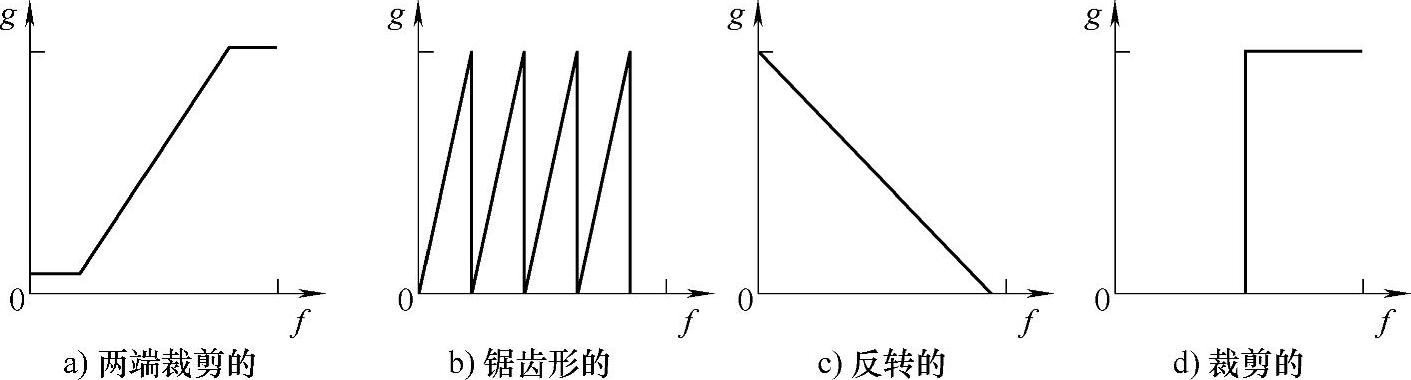
图3.15 四种典型的分段线性灰度变换函数
（3）非线性灰度变换
非线性灰度变换所采用的变换函数为非线性函数，常用的非线性灰度变换为指数灰度变换、对数灰度变换及指数和对数组合的灰度变换。
指数灰度变换是指输出图像g（x，y）与输入图像f（x，y）的灰度变换关系为指数形式，即
指数灰度变换用于压缩输入图像中低灰度区的对比度，而扩展高灰度区的对比度，其曲线形状如图3.16a所示。为了增加灰度变换的动态范围，修改曲线的起始位置或变化速率等，可加入一些调节参数，例如
式中，a、b、c均为可调参数。参数a可以控制曲线的起始位置；参数c可以改变曲线的变换率。
对数灰度变换就是输出图像g（x，y）与输入图像f（x，y）的灰度关系为对数形式，其表达式为
g（x，y）=alg[f（x，y）+1] （3.57）
对数的底可以根据需要灵活选择。在实际应用中，一般取自然对数灰度变换。对数灰度变换用于压缩输入图像中高灰度区的对比度，而扩展低灰度区的对比度，曲线形状如图3.16b所示。为了增加灰度变换的动态范围和灵活性，修改曲线的起始位置或变化速率等，对数灰度变换也可以加入一些调节参数，例如
g（x，y）=b+alg[f（x，y）+1-c] （3.58）
式中，a、b、c均为可调参数。
指数与对数组合的灰度变换就是输入图像的某个区间采用对数灰度变换，而其他区间采用指数灰度变换的灰度变换方式。如果输出图像g（x，y）的0→m灰度区与输入图像f（x，y）的0→n灰度区之间的灰度关系为指数形式，而其余区域之间的灰度关系为对数形式，其表达式可以表示为
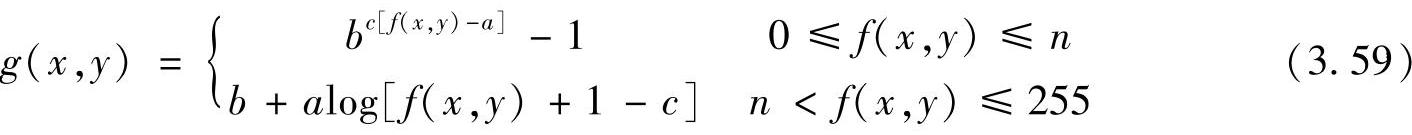
该灰度变换用于压缩输入图像中高、低灰度区两端的对比度，而扩展中间灰度区的对比度。曲线形状如图3.16c所示的实线。
如果输出图像g（x，y）的0→m灰度区与输入图像f（x，y）的0→n灰度区之间的灰度关系为对数形式，而其余区域之间的灰度关系为指数形式，则其表达式可以表示为
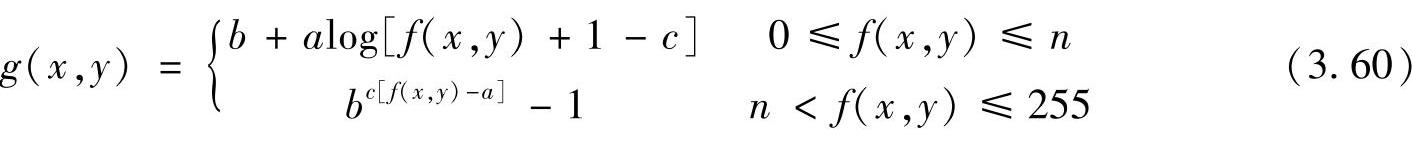
此时，对数与指数的组合灰度变换曲线如图3.16c中的虚线所示。它用于压缩中间段灰度区的对比度，而扩展高、低灰度的对比度。
图3.16 非线性灰度变换的变换函数曲线
有关视觉测量技术的文章
- 详细阅读
-
频域增强与同态滤波的视觉测量技术详细阅读
巴特沃思高通滤波具有截止频率D0的n阶巴特沃思高通滤波器的传递函数为式中，D（u，v）仍由式或式定义。图3.24 各种高通滤波器的特性曲线2.同态滤波同态滤波一种增强图像对比度的频域处理方法，尤其适合于处理由于光照不均导致的图像不清。同态滤波以式所给的图像模型为基础，在频域中同时进行图像对比度增强和压缩图像亮度范围。图3.28 同态滤波增强......
2023-11-24
- 详细阅读
-
视觉测量技术的研究目标详细阅读
借鉴人类视觉的原理，计算机视觉技术研究的长远目标是建立通用的视觉系统。计算机视觉技术的优势不仅在于能模拟人眼的功能，还能完成人眼所不能胜任的工作。因此，对人脑视觉的充分理解将促进对计算机视觉更深入的研究，并对计算机视觉系统提供坚实的生物理论基础。......
2023-11-24
-
视觉测量技术：计算机视觉测量方案详细阅读
计算机视觉测量技术以图像传感器为手段检测空间物体的空间三维坐标，进而检测物体的尺寸、形状和运动状态等。美国、加拿大、日本等发达国家早在20世纪60年代后期就已经开始了计算机视觉测量技术的研究。直到20世纪90年代，随着计算机技术的发展成熟，计算机视觉测量技术逐渐成为一个研究热点。......
2023-11-24
-
Marr视觉理论简介：视觉测量技术详细阅读
下面简要介绍Marr视觉理论的基本思想和框架。图1.1 Marr视觉信息处理的三个阶段第一阶段是早期视觉处理，其目的是从输入的原始图像中抽取观察者周围景物表面的物理特性，如距离、表面方向、材料特性等，并构成要素图或基元图。表1.2 由图像恢复形状信息的表达框架3.Marr视觉理论的意义及不足Marr视觉理论是计算机视觉研究领域的划时代成就。图1.2 改进后的Marr视觉理论框架限于历史等因素，Marr没有研究如何用数学方法严格地描述视觉信息的问题。......
2023-11-24
-
主要研究内容-计算机视觉技术的视觉测量技术详细阅读
系统标定等研究内容一般也在这个层次上进行。它要求图像技术工作在一个整体的框架下进行。图像处理是底层操作，它主要在图像的像素级上进行处理，处理数据量大。图1.3 图像工程的三层次示意......
2023-11-24
-
常用人工标记-视觉测量技术详细阅读
白色背景下的黑色普通标志是视觉测量或近景数字摄影测量常用的人工标志。工业数字摄影测量使用彩色标志是利用光的相减混色法。图2.51 白色光照射红色标志示意图通过相减混色可以有效地对彩色标志进行识别，不足之处是丢失标志的空间分辨率。如图2.51所示，白光照射红色标志，红色标志吸收的青色，只有红色光返回，在图像中形成红色标志图像。......
2023-11-24
相关推荐