这一节,我们将介绍傅氏变换的几个重要性质,为了叙述方便,假定以下需求傅氏变换的函数都满足傅氏积分定理中的条件.1.线性性质设F1(w)=F[f1(t)],F2(w)=F[f2(t)],α,β是常数,则由于傅氏变换,傅氏逆变换是由积分定义的,而积分具有线性性质,所以傅氏变换,傅氏逆变换也具有线性性质.2.位移性质设F[F(t)]=F(w),则这个性质也称为时移性,它表明时间函数f(t)沿t 轴向左或......
2025-09-30
二维离散傅里叶变换的性质及应用
【摘要】：二维离散傅里叶变换有多种性质，这里仅介绍三种：可分离性、可计算性及移位性。图3.9 由2步一维离散傅里叶变换计算二维离散傅里叶变换移位性通常在二维离散傅里叶变换之前，将输入图像乘以（-1）x+y。它是二维离散傅里叶变换设置的M×N区域的中心。当在计算机中使用二维离散傅里叶变换时，总和的范围为（u=0，…
二维离散傅里叶变换有多种性质，这里仅介绍三种：可分离性、可计算性及移位性。
（1）可分离性
二维离散傅里叶变换为可分离变换，二维离散傅里叶变换可以写成如下形式：
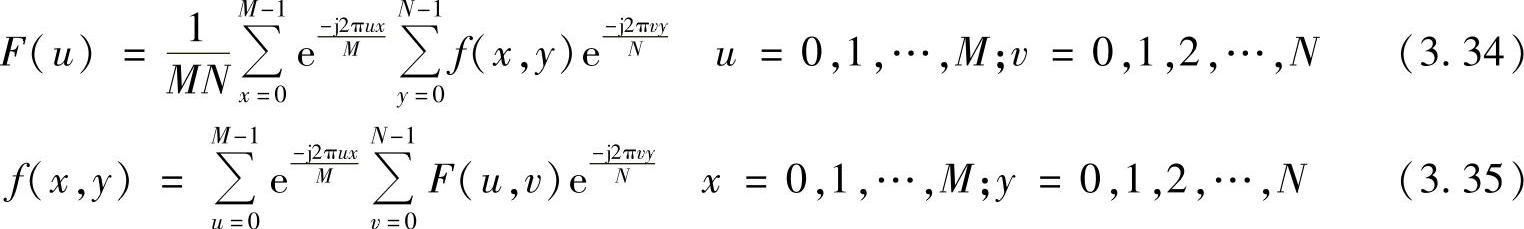
（2）可计算性
由二维离散傅里叶变换的分离形式可知，一个二维离散傅里叶变换可由连续两次运用一维离散傅里叶变换实现。也就是说，二维离散傅里叶变换可写为
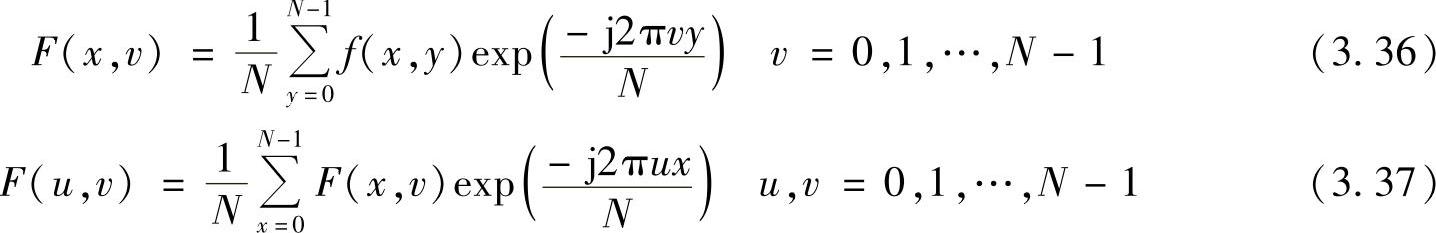
对每个x值，式（3.37）是一个一维离散傅里叶变换，所以F（x，v）可由沿f（x，y）的每一列求变换得到。在此基础上，对F（x，v）每一行求一维离散傅里叶变换即得到F（u，v）。该过程可用图3.9表示。(https://www.chuimin.cn)
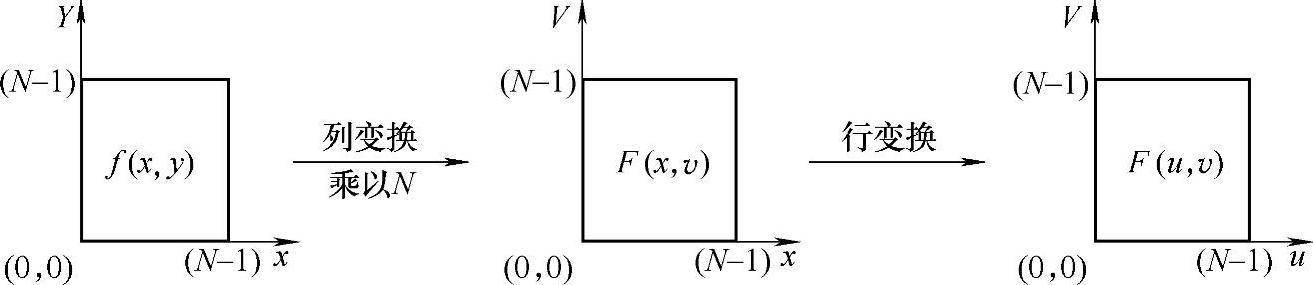
图3.9 由2步一维离散傅里叶变换计算二维离散傅里叶变换
（3）移位性
通常在二维离散傅里叶变换之前，将输入图像乘以（-1）x+y。由于指数的性质，容易得到
式（3.38）说明f（x，y）（-1）x+y的二维离散傅里叶变换的原点，即F（0，0）被设置在u=M/2、v=N/2上。
换句话说，（-1）x+y乘以f（x，y）将F（u，v）的原点变换到频率坐标下为[M/2，N/2]。它是二维离散傅里叶变换设置的M×N区域的中心。将此频率域的范围指定为频率矩形，它从u=0到u=M-1，从v=0到v=N-1。为了确保移动后坐标为整数，要求M和N为偶数。当在计算机中使用二维离散傅里叶变换时，总和的范围为（u=0，…，M-1），（v=0，…，N-1）。实际的变换中心将为u=M/2+1，v=N/2+1。
相关文章
- 详细阅读
-
非线性算子的性质及应用详细阅读
非线性算子的性质包括连续性、有界性、全连续性、可微性等.这是一些基本概念和性质,在后面各章中都要用到.设E1和E2时两个实Banach 空间,D E1.设A∶D→E2为非线性的.定义1设x0∈D.若ε>0,δ=δ(x0,ε)>0 使得当x ∈D且‖x-x0‖ < δ 时,恒有‖Ax -Ax0‖ < ε,则称A 在x0连续;若A 在D 中每一点都连续,则称A 在D 上连续;若上述δ 只与ε 有关而......
2025-09-30
-
基于二维傅里叶变换的内插模板优化技术详细阅读
正交基为傅里叶算子时，模板设计过程与上面沃尔什算子基本相同，不同之处在于卷积类型变为循环卷积。傅里叶基设计的特点是可以构造任何大小的内插模板，而不限于2的整数次幂。......
2025-09-29
-
幂函数的规定及性质-复变函数及其应用详细阅读
定义3 设α是任意一个复数,定义幂函数为w =zα =eαLnz(z 0).在α为正实数时,对z =0的情况进行规定：zα =0.幂函数是指数函数与对数函数的复合函数,根据对数函数的定义,有w =zα =eαLnz =eα(ln z+2kπi) =eα ln z·e2αkπi,(k为整数)由于Lnz = ln z+2kπi是多值的,所以w = zα也是多值的,且所取的不同数值的个数等于e2αkπi......
2025-09-30
-
傅里叶变换的性质-傅里叶光学原理与系统设计详细阅读
以一维函数为例，介绍傅里叶变换的主要性质，这些性质可以直接推广到二维函数。这一性质可由傅里叶变换定义式中积分运算的线性性导出。......
2025-09-30
-
二维正态分布的性质及解析2015考研数学基础详细阅读
【主要内容】服从二维正态分布的随机变量有以下常用的性质：（1）设（X，Y）～N（μ1，μ2，σ21，σ22，ρ），则X～N（μ1，σ21），Y～N（μ2，σ22）；反之，如果X与Y相互独立，且X～N（μ1，σ21），Y～N（μ2，σ22），则（X，Y）～N（μ1，μ2，σ21，σ22，0）（注意：这个结论中X与Y相互独立的条件是不可缺少的）.（2）设（X，Y）～N（μ1，μ2，σ21，σ22，ρ）......
2025-09-30
-
正弦函数性质及解析-机电应用数学详细阅读
由正弦函数y=sinx的图像可知：定义域正弦函数y=sinx的定义域是R.值域正弦函数y=sinx，x∈R的值域是[-1，1]，即对任意的x∈R，都有-1≤sinx≤1.其中，当，k∈Z，有ymax=1；当，k∈Z时，有ymin=-1.想一想等式2sinx=3，，都成立吗？例2求出下列函数的最大值和最小值：y=1-sinx； y=2sinx.解：当sinx=-1时，ymax=1-（-1）=2；当sinx=1时，ymin=1-1=0.当sinx=1时，ymax=2×1=2；sinx=-1时，ymin=2×（-1）=-2.想一想第题中的函数y=1-sinx取得最大值和最小值时，对应的x的取值集合分别是什么？......
2025-09-30
-
拉氏变换性质|复变函数及应用详细阅读
这一节将介绍拉氏变换的几个基本性质,它们在拉氏变换的实际应用中都是很有用的.为了叙述方便,假定在这些性质中,凡是要取拉氏变换的函数都满足拉氏变换存在定理中的条件,并且把这些函数的增长指数统一地设为c.在证明这些性质时,不再重复这些条件.1.线性性质设α,β为常数,且则有或2.相似性质设a ＞0,若L[f(t)]=F (p),则类似有以上两条性质的证明与傅氏变换相应的性质的证明是一样的.3.微分性质......
2025-09-30
相关推荐