首页理论教育一维离散傅里叶变换在视觉测量技术中的应用

一维离散傅里叶变换在视觉测量技术中的应用

2023-11-24 理论教育版权反馈

【摘要】：对所有M个u值重复这一过程，可以获得完整的离散傅里叶变换。用离散傅里叶变换可求出与M个采样点对应的M个频域点。若已知F，则可以利用离散傅里叶反变换得到原函数f，即式和式共同构成一个离散傅里叶变换对。图3.8 简单的M个点离散函数f及其一维离散傅里叶变换幅度谱

若以Δx为采样间隔，对连续函数f（x）进行等间隔采样，将得到N个离散的函数值{f（x₀），f（x₀+Δx），f（x₀+2Δx），…，f（x₀+（N-1）Δx））。其中，每一个函数值称为f（x）的一个样本。为了表示方便，表示为

f（x）=f（x₀+xΔx）（3.16）

式中，x的取值为离散值0，1，…，N-1。

那么被采样的单变量离散函数f（x）的傅里叶变换为

式中，j为虚数单位；u为频率变量。空间域f（x）经式（3.17）变换后所得到的空间称为函数的频域空间（简称频域）。为了计算F（u），首先在指数项中代入u=0，然后将所有x相加。接下来在指数项中代入u=1，重复对所有x相加。对所有M个u值重复这一过程，可以获得完整的离散傅里叶变换（Discrete Fourier Transform，DFT）。用离散傅里叶变换可求出与M个采样点对应的M个频域点。即u取值为-M/2～M/2，可以得到关于原点轴对称的频谱。如u取值范围为0～M，则取正方向频率。

若已知F（u），则可以利用离散傅里叶反变换得到原函数f（x），即

式（3.17）和式（3.18）共同构成一个离散傅里叶变换对。变量u有相似的解释，F（u）序列一般从0频率开始。因此，u值序列为{0，Δu，2Δu，…，[M-1]Δu}。F（u）理解为

式中，u=0，1，…，M-1。变换前的1/M乘数有时放在反变换前。有时变换和反变换都乘以1/M。由傅里叶变换可得u=0的变换值为

可见F（0）是f（x）的平均值，因此F（0）有时被称作频率谱的直流成分。

在一维离散傅里叶变换中，时域的采样频率Δx和频域的采样频率Δu的关系为

一个实函数的一维离散傅里叶变换通常是复数，一维离散傅里叶变换可以用极坐标形式表示为

F（u）=Re（u）+iIm（u）（3.22）式中，Re（u）和Im（u）分别是F（u）的实部和虚部。利用欧拉关系可以将式（3.22）表示为极坐标形式，即

F（u）=|F（u）|e^jϕ（u）（3.23）(www.chuimin.cn)

式中

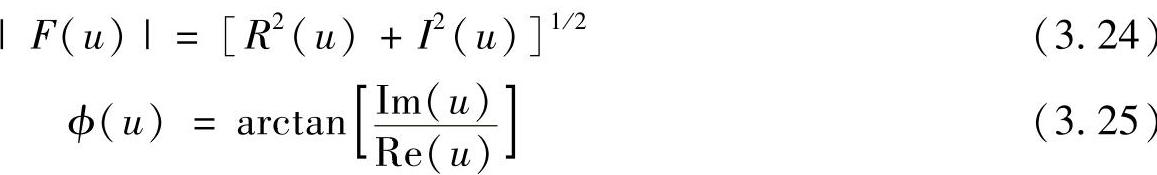
其中，|F（u）|被称为傅里叶变换的幅度或幅度谱（简称为谱）；|ϕ（u）|被称为傅里叶变换的相角或相位谱。幅度谱与相位谱统称为信号的频谱。谱的二次方被称为功率（功率谱，能量谱），其定义为

P（u）=F²（u）=R²（u）+I²（u）（3.26）

信号分析中的“谱密度”也是指功率谱。

【例3.5】傅里叶变换实例

图3.8给出了一个M个点离散函数f（x）及其一维离散傅里叶变换幅度谱。图3.8a所示的离散信号的非0点个数为K，图3.8b显示了其傅里叶变换的幅度谱|F（u）|；图3.8c所示的离散信号的非0点个数为2K，图3.8d显示其相应的一维离散傅里叶变换的幅度谱|F（u）|。

对于图3.8a所示的函数，其傅里叶变换为

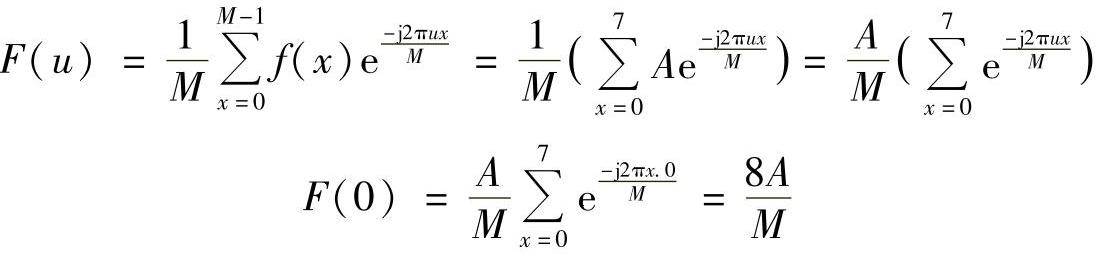
对于图3.8c所示的函数，其傅里叶变换为

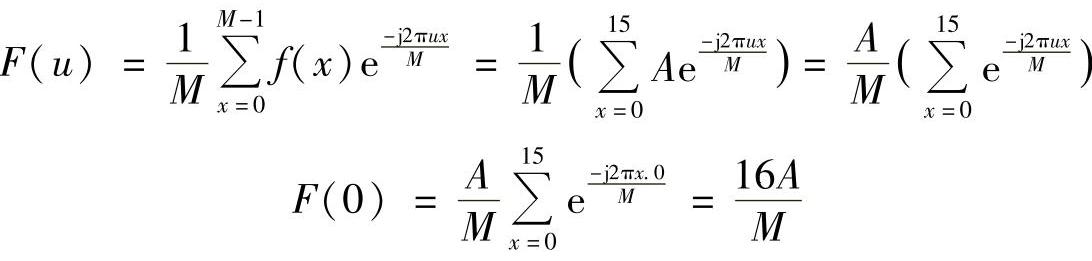
从这两个信号的幅度谱可以看出：

1）当函数曲线下的面积在x域加倍时，傅里叶变换幅度谱的高度加倍。

2）当函数的长度加倍时，相同间隔下幅度为0的频率点数量加倍。

需要说明的是，如果离散信号f（x）在变换前被乘以（-1）x，则频率谱的中心将被移动到u=M/2处。

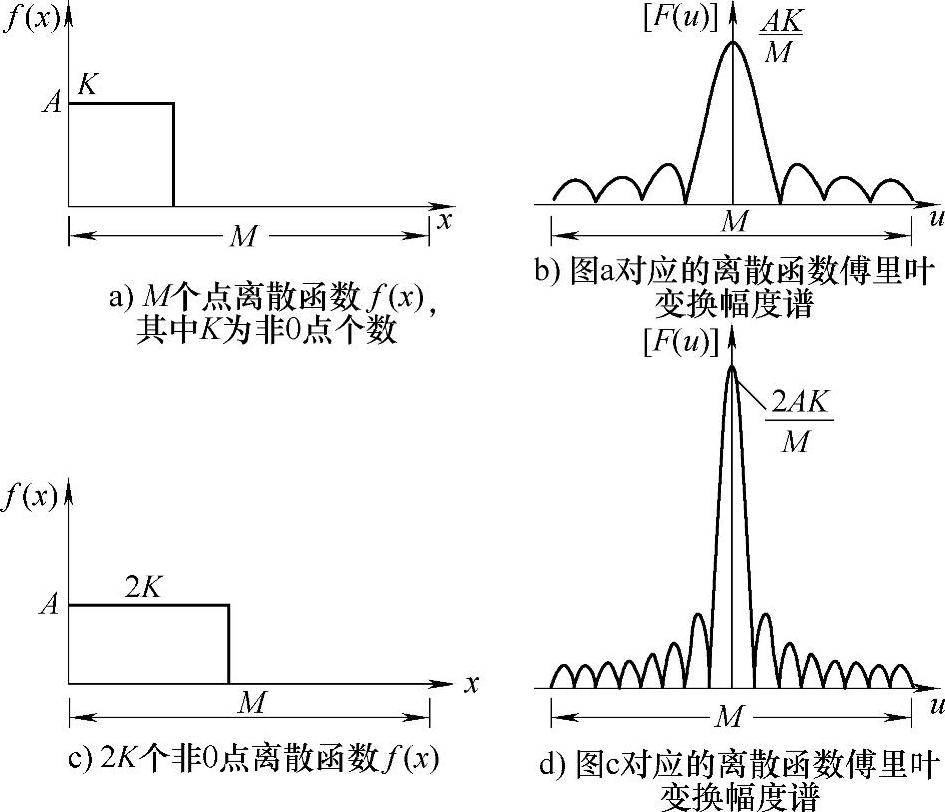
图3.8 简单的M个点离散函数f（x）及其一维离散傅里叶变换幅度谱