视觉测量技术中的空间域滤波方法及应用

2023-11-24 理论教育版权反馈

【摘要】：线性空间域滤波借助模板与图像进行卷积并在邻域操作。图3.5a所示为一个3×3的均值滤波器，将其应用于图3.4a的子图像，其滤波结果为对于与图3.3b所示模板对应的像素区域，采用图3.5a所示的滤波器进行滤波，其结果为均值滤波器减小了图像灰度的“尖锐”变化。非线性空间域滤波器能够较好地处理椒盐噪声、脉冲噪声和孤立噪声点。中值滤波器的使用图3.6所示是利用3×3的模板进行中值滤波的示例。

空间域滤波即直接在图像空间中进行滤波操作，空域滤波有时借助变换域实现。例如，线性系统的转移函数和脉冲函数或点扩散函数构成傅里叶变换对，所以线性系统滤波器的设计常借助于傅里叶变换分析，即在频域完成滤波器的设计，然后反变换回空间域构造滤波器模板，采用滤波器模板卷积图像实现滤波操作。

空间域滤波是在图像空间借助模板进行邻域操作完成的，即在待处理图像中逐点移动模板。在每一点（x，y）处，滤波器在该点的响应通过事先定义的关系进行计算。

空间域滤波分为线性空间域滤波和非线性空间域滤波。线性空间域滤波借助模板与图像进行卷积并在邻域操作。非线性空间域滤波则直接在邻域操作。

1.线性空间域滤波

线性空间域滤波是一种对高斯噪声有效的滤波方法。它借助模板（也称为掩模、卷积核或滤波器）与图像进行卷积来实现。线性空域滤波的模板的系数和为1，在图像平坦区域模板输出与原值相同，具有低通滤波的特性。在图像的每一点（x，y）处，计算模板与所覆盖图像区域的线性输出响应，并将响应结果赋予模板所覆盖区域中心的像素值。

假设模板W的大小为m×n，图像f的大小为M×N，线性空间域滤波的主要操作过程可以描述如下：

1）将模板在图像中漫游，遍历图像中每个像素，并将模板中心与图像中某个像素位置重合。图3.3给出了一个用3×3模板进行图像遍历滤波的示例。

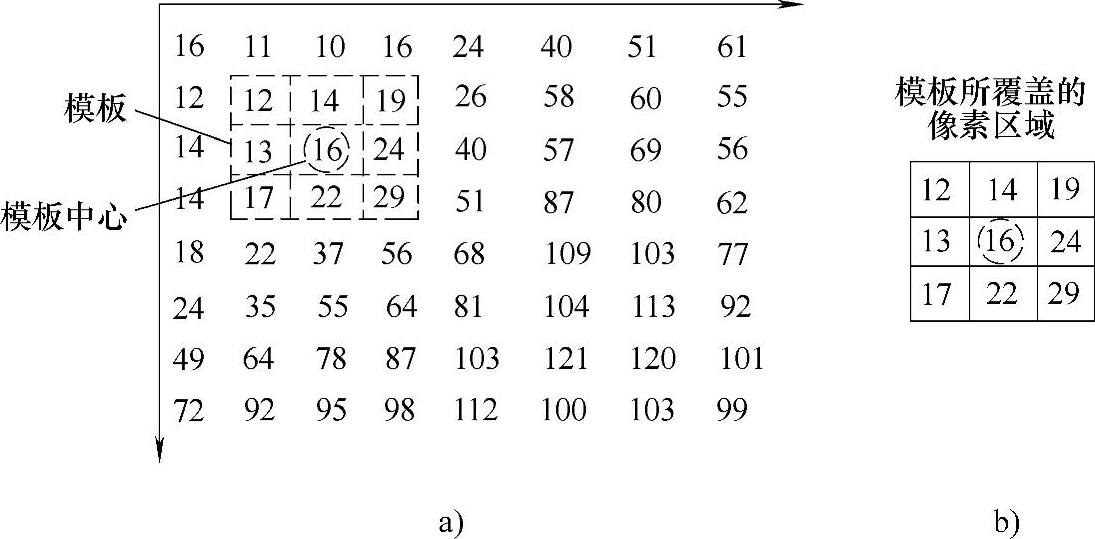
图3.3 用3×3模板进行图像遍历滤波的示例

2）将模板系数（见图3.4b）与模板所覆盖区域的对应像素（其位置编号如图3.4a所示）相乘并将所有乘积相加，即可按照下式计算模板W在图像（x，y）处的响应：

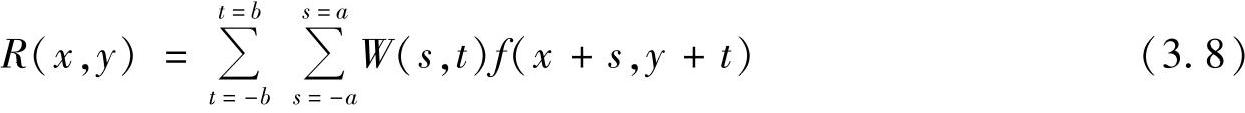
式中，a=（m-1）/2，b=（n-1）/2，a、b为非负整数。一般情况下，模板的长和宽都是奇数，其有意义的最小尺寸为3×3。为了保证在无噪声区域模板卷积的输出保持图像原值不变，W（s，t）应该满足如下的归一化条件：

3）将R（x，y）赋给去噪后所得新图像中（x，y）位置的像素值g（x，y），如图3.4c所示。

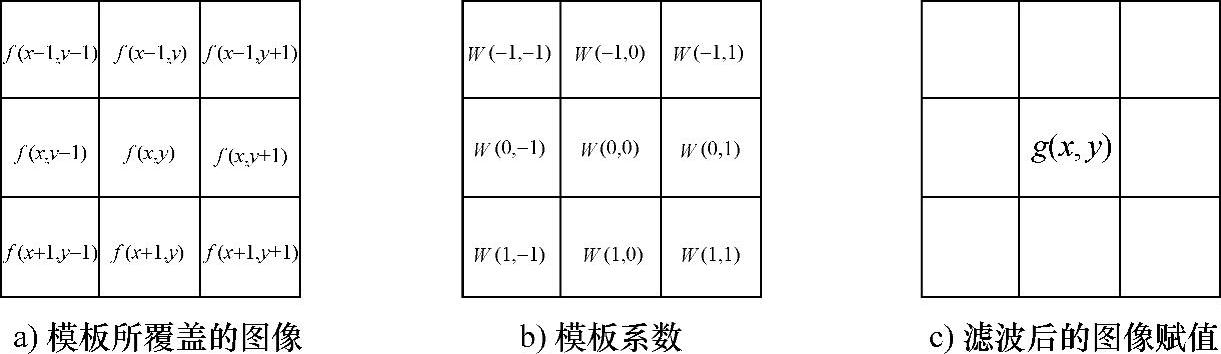
图3.4 线性空间域滤波的模板及所覆盖像素位置

根据模板系数的不同，可以将线性空间域滤波分为均值线性空间域滤波（以下简称为均值滤波）与加权均值线性空间域滤波（以下简称为加权均值滤波）两种。其中，均值滤波器中的各个模板系数完全相同，而加权均值滤波器中各个模板系数依据离模板中心的远近而不同。

【例3.1】均值滤波器使用实例

均值滤波器模板系数相等，且和为1。其输出响应是包含滤波模板邻域内像素的平均值，即用滤波模板确定的邻域内像素的灰度平均值去代替图像中每个像素点的值。

图3.5a所示为一个3×3的均值滤波器，将其应用于图3.4a的子图像，其滤波结果为

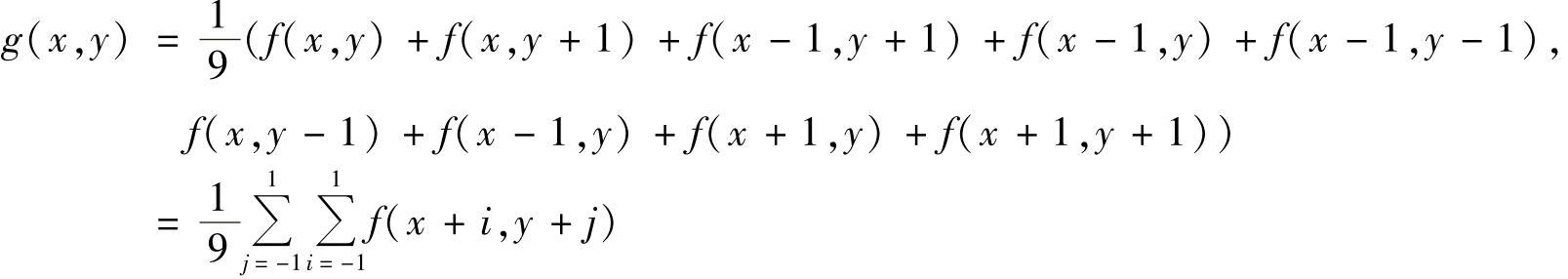
对于与图3.3b所示模板对应的像素区域，采用图3.5a所示的滤波器进行滤波，其结果为

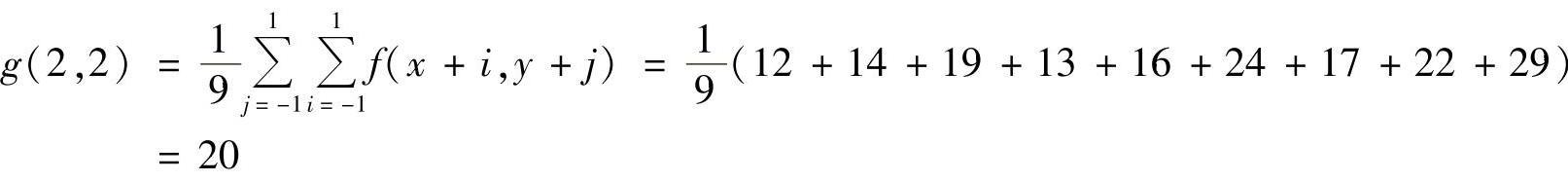
均值滤波器减小了图像灰度的“尖锐”变化。由于图像边缘也是图像中灰度剧烈变化的地方，因此在滤波过程中均值滤波处理会使图像边缘产生一定的模糊。均值滤波主要关注的是模板的形状和尺度，而不是模板系数。

【例3.2】加权均值滤波器使用实例

与均值滤波器相比，加权均值滤波器的模板系数可以不同，但其模板系数之和仍为1。一般来说，距离模板中心越远，模板系数越小。也就是说，在计算图像中某点的新像素值时，处于模板中心位置的像素比其他任何像素的作用都要大。加权均值模板可以有效减小平滑处理中图像边缘的模糊效应。

图3.5b给出了一个加权均值滤波器，将其应用于图3.4a中的子图像，则模板的输出响应为

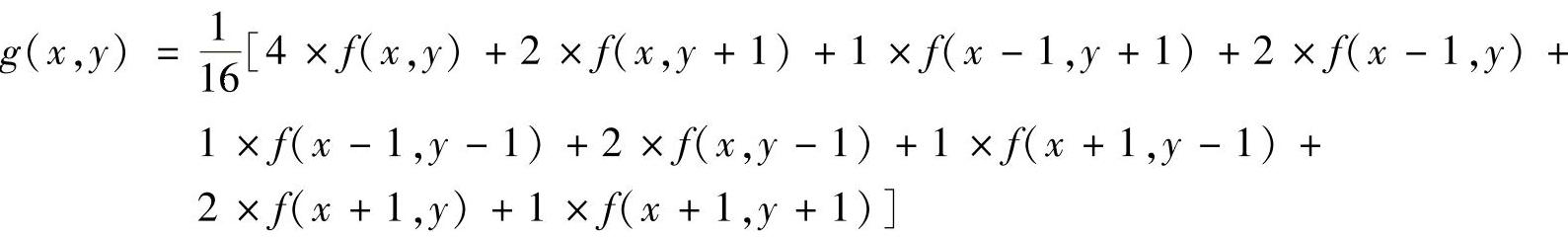
对于图3.3b中模板所对应的像素区域，采用图3.5b所示的加权均值滤波器进行滤波，其结果为

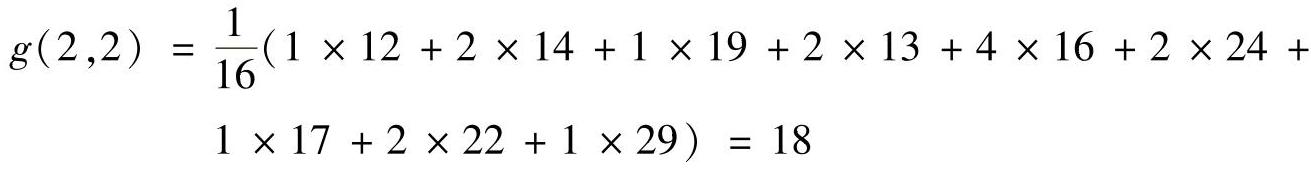
2.非线性空间域滤波

线性空间域滤波可以有效地去除高斯噪声，但在消除噪声的同时也会使图像中的一些细节变得模糊。很多情况下，图像中的一些噪声点通常比非噪声点的像素更亮或更暗，可以用脉冲噪声或椒盐噪声来描述。这时如果在噪声点像素周围寻找一个合理的数值对它进行代替，在一定程度上可以获得较理想的滤波结果。中值滤波、最大值滤波和最小值滤波等都是基于上述思想进行滤波的算法，它们都是典型的非线性滤波方法。非线性空间域滤波器能够较好地处理椒盐噪声、脉冲噪声和孤立噪声点。非线性空间域滤波的一般操作步骤如下：

图3.5 两个3×3的滤波器

1）将模板在图中漫游，遍历图像中每个像素，并将模板中心与图像中某个像素位置重合。

2）读取模板下一个对应像素的灰度值。

3）将这些灰度值从小到大排成一列。

4）找出这些值里排在中间的某一个值。

5）将这个中间值赋给对应模板中心位置的像素。

（1）中值滤波器

中值滤波的基本思想是，首先确定一个尺寸为奇数的m×n的模板W，模板所覆盖的像素按灰度值从小到大排序后，用中间位置灰度值代替原灰度值。因此其基本步骤描述如下。

1）将模板在图中漫游，遍历图像中每个像素，在每个像素位置将模板中心与该像素重合，如图3.3a所示。

2）读取模板对应的图像子块中每一个像素的灰度值。

3）将这些灰度值从小到大排成一列。(www.chuimin.cn)

4）找出这些值里排在中间的值，并将这个中间值赋给对应模板中心位置的像素，即中值滤波后的图像在（x，y）的灰度值为

g（x，y）=median{f（x′，y′）} （3.10）

式中，x′∈[x-m+1，x+m-1]；y′∈[y-n+1，y+n-1]；m与n为选定的模板大小。

通过上述步骤可以看出，中值滤波器的主要功能就是让与周围像素灰度值的差比较大的像素改为与周围像素灰度值接近的像素，所以它对孤立噪声像素的消除能力很强。由于它不是简单地取平均，所以产生的模糊比较少。换句话说，中值滤波器既能消除噪声，又能保持图像的细节。

【例3.3】中值滤波器的使用

图3.6所示是利用3×3的模板进行中值滤波的示例。图3.6a所示为图3.3中模板所覆盖的一个图像区域，将9个像素按照从小到大的顺序进行排列，其排列结果如图3.6c所示。由于17排在中间，因此最终模板中心所对应的像素f（2，2）的值用17代替，即g（2，2）=17。

（2）最大值滤波器和最小值滤波器

中值相当于顺序排列数值中间的数，如果使用排序序列中最后一个数值，即得到最大值滤波器，其表达式为

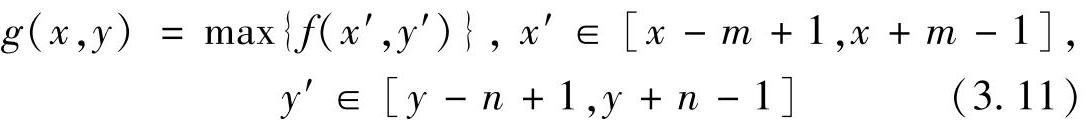
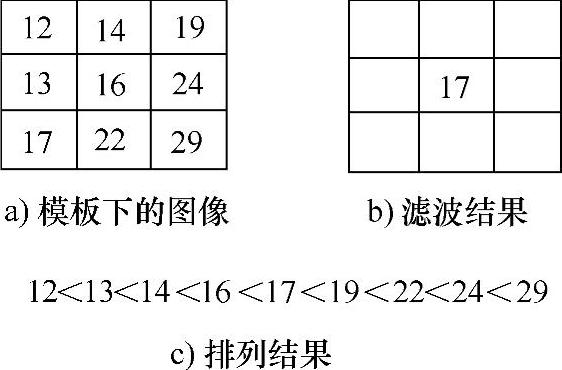
图3.6 用3×3模板进行中值滤波示例

最大值滤波器在发现图像中的最亮点时非常有用。因为“胡椒”噪声是非常低的值，可以通过最大值滤波器消除“胡椒”噪声。

选择排序序列中起始位置数值的滤波器称为最小值滤波器，其表达式为

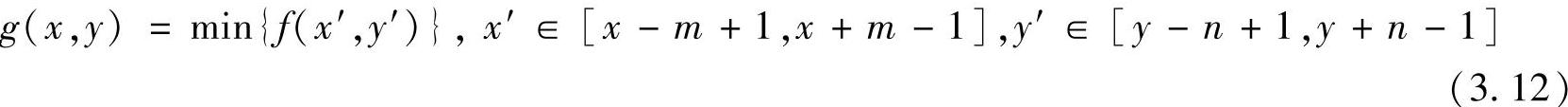
最小值滤波器对发现图像中的最暗点非常有用。因为“盐粉”噪声是非常高的值，因此可以利用最小值滤波器来消除“盐粉”噪声。

【例3.4】最大值滤波器和最小值滤波器使用示例

在图3.6a所示的图像中，若使用最大值滤波器，由于9个像素中的最大值为29，因此模板中心所对应的像素值应为29，即g（2，2）=29。

同理，在图3.6a所示的图像中，若使用最小值滤波器进行滤波，由于9个像素中的最大值为12，因此模板中心所对应的像素值应为12，即g（2，2）=12。

（3）中点滤波器

中点滤波器是在滤波器涉及范围内计算最大值和最小值之间的中点，其计算表达式为

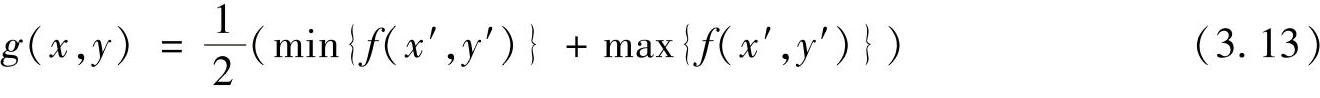
式中，x′∈[x-m+1，x+m-1]；y′∈[y-n+1，y+n-1]。

在图3.6a所示的图像中，若使用中点滤波器，由于9个像素中的最大值为29，最小值为12，因此滤波后模板中心所对应的像素的值应为21（四舍五入）。

由于中点滤波器结合了顺序统计和求平均，因此对于高斯噪声和均匀分布噪声有较好的效果。

（4）修正后的阿尔法均值滤波器

修正后的阿尔法均值滤波器也叫阿尔法裁减均值滤波器。它是结合均值滤波器和非线性滤波器形成的裁减滤波器，对脉冲噪声和高斯噪声的混合噪声有效。

假设在f（x，y）邻域内去掉d/2个具有最高灰度值的像素和d/2个具有最低灰度值的像素，用f_r（x，y）代表剩余的mn-d个像素。由这些剩余像素点的平均值形成的滤波器称为修正后的阿尔法均值滤波器，其表达式为

式中，d值可以取0到mn-1之间的任意数。

当d=0时，修正后的阿尔法均值滤波器变为算术均值滤波器。

当d=（mn-1）/2时，修正后的阿尔法均值滤波器将变为中值滤波器。

在图3.6a所示的图像中，若使用修正后的阿尔法均值滤波器进行滤波，假设d=4，去掉两个最大值（29和24），两个最小值（12和13），取剩下五个像素的均值作为模板中心像素的最终灰度值，即g（2，2）=（14+16+17+22+24）/5=19（四舍五入）。

3.应注意的问题

应用空间域滤波法进行图像平滑时要注意以下两个问题：模板尺寸的选取与边界处理。

模板尺寸与平滑效果直接相关。一般而言，模板越大，平滑效果越好，但会造成图像边缘信息的损失。因此，模板的大小应该在保证消除噪声的前提下尽可能地保持图像的边缘信息。在实际应用中，模板尺寸一般设定为奇数，且不超过11×11，可以选择3×3、5×5、7×7等。2×2的模板有时也会用到，此时模板与所覆盖的像素位置关系如图3.7所示。

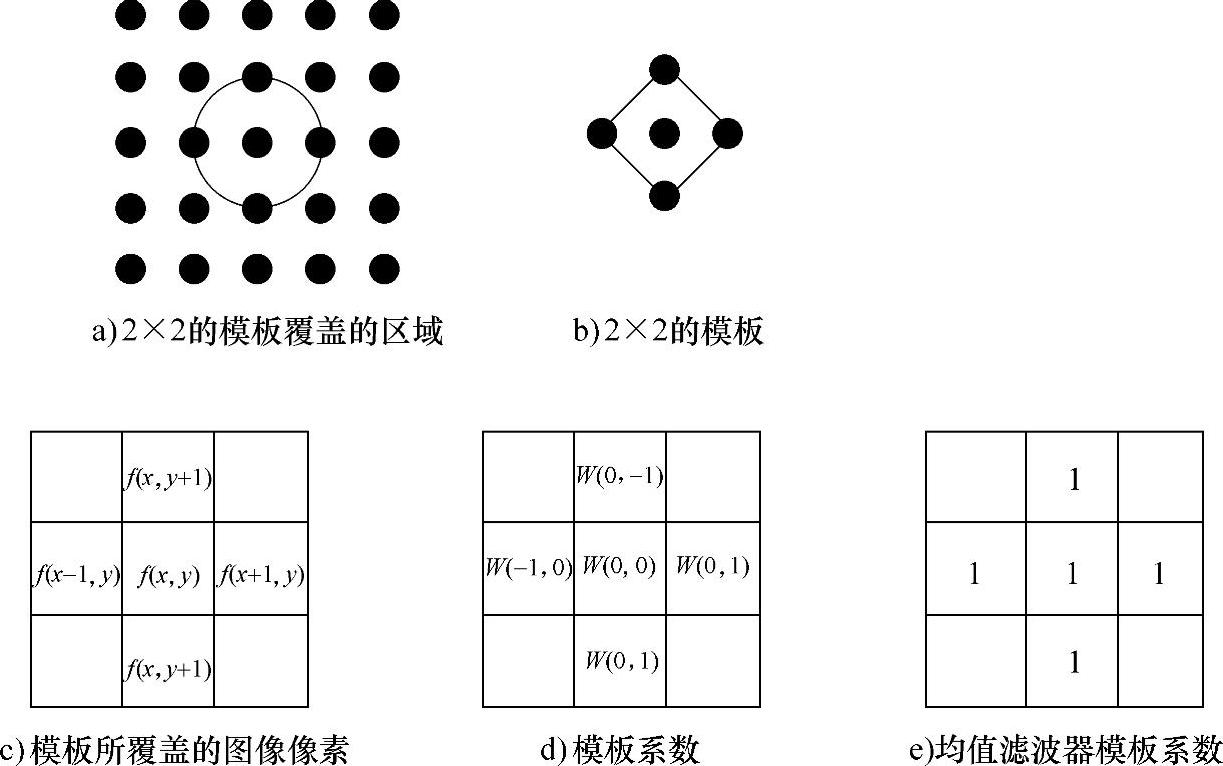
图3.7 2×2的模板

此时，其滤波器响应输出为

实现空间滤波邻域处理时的另一个重要考虑因素是边界处理，即当滤波中心靠近图像边界时如何进行计算。考虑一个简单的大小为n×n的方形模板，当模板中心距离图像边缘为（n-1）/2个像素时，该模板至少有一条边与图像边界重合。如果模板中心继续向图像边界靠近，那么模板的行或列就会处于图像平面之外。对于这个问题一般有如下处理方法：

1）将模板中心点的移动范围限制在距离图像边界不小于（n-1）/2个像素处。这种方法处理后的图像比原始图像略小。但滤波后的图像中的所有像素点都由整个模板处理。

2）用全部包含于图像中的模板部分滤波所有像素。通过这种方法，处理后的图像的大小与原始图像尺寸大小一致。靠近边界部分的像素带将用部分滤波模板来处理。

3）在图像边界以外，再补上一行和一列灰度为零的像素点，其灰度也可以为其他常值，或者将边界复制补在图像之外。补上的部分经过处理后去除，保持处理后图像与原始图像尺寸大小相等。但是补在靠近图像边缘的部分会带来不良的影响。这种影响随着模板尺寸的增加而增大。

视觉测量技术中的空间域滤波方法及应用

相关推荐