如何判断逻辑函数是否相等

2023-11-24 理论教育版权反馈

【摘要】：若两个逻辑函数具有相同的真值表，则认为该两个逻辑函数相等。有时多出一项后，反而有利于化简逻辑函数。

1.逻辑函数定义

输入输出变量为逻辑变量的函数称为逻辑函数。

在数字电路中，逻辑变量只有逻辑0和逻辑1两种取值，它们之间没有大小之分，不同于数学中的0和1。

2.逻辑函数的表示方法

逻辑函数的表示方法主要有真值表、逻辑表达式、逻辑电路图、卡诺图和波形图等。

（1）真值表。

真值表是将输入逻辑变量各种可能的取值和相应的函数值排列在一起而组成的表格。

n个逻辑变量可列出2ⁿ种状态，按0→（2ⁿ-1）排列。既不能遗漏，又不能重复。

（2）逻辑表达式。

逻辑表达式是用各逻辑变量相互间与、或、非逻辑运算组合表示的逻辑函数，相当于数学中的代数式、函数式。

书写逻辑表达式的方法是：把真值表中逻辑值为1的所有项相加（逻辑或）；每一项中，A、B、C的关系为“与”，变量值为1时取原码，变量值为0时取反码。

（3）逻辑电路图。

逻辑电路图是用规定的逻辑电路符号连接组成的电路图。

（4）卡诺图。

卡诺图是按一定规则画出的方格图，是真值表的另一种形式，主要用于化简逻辑函数。

（5）波形图。

波形图是逻辑函数输入变量每一种可能出现的取值与对应的输出值按时间顺序依次排列的图形，也称为时序图。波形图可通过实验观察，在逻辑分析仪和一些计算机仿真软件工具中，常用这种方法给出分析结果。

真值表、逻辑表达式、逻辑电路图、卡诺图和波形图具有对应关系，可相互转换。对同一逻辑函数，真值表、卡诺图和波形图具有唯一性；逻辑表达式和逻辑电路图可有多种不同的表达形式。

3.逻辑函数的有关概念

（1）最小项。

定义：真值表中所有输入变量的组合称为最小项。

特点：①n个逻辑变量有2ⁿ个最小项。②每项都包括了所有输入逻辑变量。③每个逻辑变量均以原变量或反变量形式出现一次。

将最小项按序编号，并使其编号值与变量组合值对应一致，记作m_i。

（2）最小项表达式。

由最小项组成的逻辑表达式称为最小项表达式，也称为与或表达式。

最小项表达式可用下式表示：F（A、B、C、…）=∑m_i

（3）最简与或表达式。

条件：①乘积项个数最少。②每个乘积项中变量最少。

（4）逻辑函数相等概念。

若两个逻辑函数具有相同的真值表，则认为该两个逻辑函数相等。(www.chuimin.cn)

4.公式法化简逻辑函数

公式法化简逻辑函数是运用逻辑代数公式，消去多余的“与”项及“与”项中多余的因子。

公式法化简一般有以下几种方法：并项法、吸收法、消去法和配项法。

（1）并项法是利用A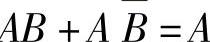将两个乘积项合并为一项，合并后消去一个互补的变量。

（2）吸收法是利用公式A+AB=A吸收多余的乘积项。

（3）消去法是利用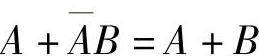消去多余的因子。

（4）配项法是利用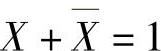，将某乘积项一项拆成两项，然后再与其他项合并，消去多余项。有时多出一项后，反而有利于化简逻辑函数。

5.卡诺图化简逻辑函数

（1）卡诺图。

卡诺图是根据真值表按相邻原则排列而成的方格图，是真值表的另一种形式。

（2）卡诺图主要特点。

①n变量卡诺图有2ⁿ个方格，每个方格对应一个最小项。

②相邻两个方格所代表的最小项只有一个变量不同。

（3）3变量和4变量逻辑函数卡诺图如图6-2a、b所示。

（4）卡诺圈合并。

卡诺图的主要功能是合并相邻项。其方法是将最小项为1（称为1方格）的相邻项圈起来，称为卡诺圈。一个卡诺圈可以包含多个1方格，一个卡诺圈可以将多个1方格合并为一项。

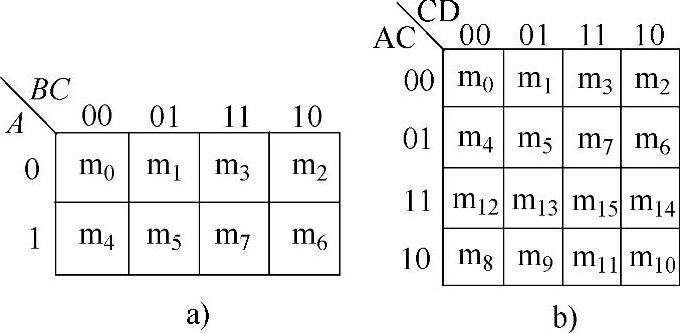
图6-2 卡诺图

a）3变量 b）4变量

（5）卡诺图化简规则。

①卡诺圈内的1方格应尽可能多，卡诺圈越大，消去的乘积项数越多。但卡诺圈内的1方格个数必须为2ⁿ个，即2、4、8、16等，不能是其他数字。

②卡诺圈的个数应尽可能少，卡诺圈数即与或表达式中的乘积项数。

③每个卡诺圈中至少有一个1方格不属于其他卡诺圈。

④不能遗漏任何一个1方格。若某个1方格不能与其他1方格合并，可单独作为一个卡诺圈；

（6）具有无关项的卡诺图化简。

具有无关项的卡诺图化简时，无关项可以视做1，也可以视做0，以有利于化得最简为前提。

（7）卡诺图化简的特点。

卡诺图化简法的优点是简单、直观，而且有一定的操作步骤可循，化简过程中易于避免差错，便于检验逻辑表达式是否化至最简，初学者容易掌握。但逻辑变量超过5个（含）时，将失去简单直观的优点，也就没有太大的实用意义了。

公式法化简的优点是它的使用不受条件限制，但化简时没有一定的操作步骤可循，主要靠熟练、技巧和经验；且一般较难判定逻辑表达式是否化至最简。

如何判断逻辑函数是否相等

相关推荐