首页理论教育正弦交流电路基本概念解析和题解

正弦交流电路基本概念解析和题解

2023-11-24 理论教育版权反馈

【摘要】：交流电流有效值：对于正弦交流电流，则有：对于我国民用正弦交流电，220V是该正弦交流电压有效值，是其幅值。与频率、周期的关系：我国民用正弦交流电，称为“工频”：f=50Hz，T=0.02s，ω=100πrad/s≈314rad/s。两个同频率正弦量之间的相位之差，称为相位差。设正弦电压，用相量表示：或。图2-2 正弦量相量图

1.正弦量三要素

以正弦交流电流为例，其表达式：i（t）=I_msin（ωt+φ）。

三要素：幅值I_m、角频率ω和初相位φ。

（1）幅值I_m和有效值I。

I_m是最大值、幅值。I是有效值，是根据电流热效应确定的，等于在同等条件下通过电阻R所产生的热量相等的直流电流值I。

交流电流有效值：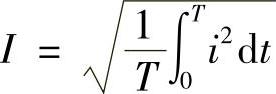

对于正弦交流电流，则有：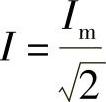

对于我国民用正弦交流电，220V是该正弦交流电压有效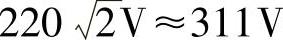值，是其幅值。

（2）角频率ω、频率f和周期T。

角频率ω表示在单位时间内正弦量所经历的电角度，单位为弧度/秒，用rad/s表示。

与频率、周期的关系：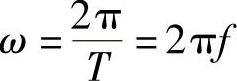

我国民用正弦交流电，称为“工频”：f=50Hz，T=0.02s，ω=100πrad/s≈314rad/s。

（3）相位角和初相位角φ（简称相位和初相位）。

正弦量某一时刻的电角度称为相位角，是时间t的函数，用（ωt+φ）表示。

φ称为初相位，是t=0时刻的相位。

（4）同频率正弦量之间的相位差。

两个同频率正弦量之间的相位之差，称为相位差。

设两个同频率正弦量u和i，其表达式分别为u=U_msin（ωt+φ_u）、i=I_msin（ωt+φ_i），则u与i相位差：φ=（ωt+φ_u）-（ωt+φ_i）=φ_u-φ_i，该式表明，两个同频率正弦量之间的相位差为其初相位之差，与ωt无关。

两个同频率正弦量之间的相位差一般有以下几种情况。

1）超前：若φ=φ_u-φ_i>0，则称u超前i（或i滞后u），如图2-1a所示。

2）滞后：若φ=φ_u-φ_i<0，则称u滞后i（或i超前u），如图2-1b所示。(www.chuimin.cn)

3）正交：若φ=φ_u-φ_i=±90°，则称u与i正交，如图2-1c所示。

4）同相：若φ=φ_u-φ_i=0，则称u与i同相，如图2-1d所示。

图2-1 两个同频率正弦量之间的相位关系

a）u超前i b）i超前u c）正交 d）同相 e）反相

5）反相：若φ=φ_u-φ_i=±180°，则称u与i反相，如图2-1e所示。

2.正弦量的相量表示法

（1）相量表达形式。

设正弦电压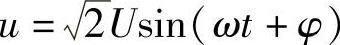，用相量表示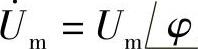：或。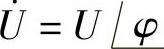

相量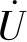的表达形式通常有两种：极坐标形式和直角坐标形式。

1）极坐标形式：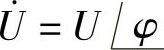

2）直角坐标形式：

其中，a=Ucosφ，b=Usinφ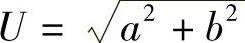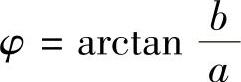；，，如图2-2所示。

注意事项：正弦量和相量是两个完全不同的概念。正弦量用相量表示，仅是表示而已。目的是借助其运算方法，便于解决正弦量之间的加减乘除问题。而且，当两个同频率的正弦相量置于同一复平面上时，可一目了然地比较它们的大小（长度）和相位关系（初相位角、越前滞后）。

（2）相量运算。

1）相量加减法，应将其化成直角坐标形式（即复数形式），实部加（减）实部、虚部加（减）虚部，然后再化成极坐标形式。

2）相量乘除法，应将其化成极坐标形式，然后模相乘（除），幅角相加（减）。

图2-2 正弦量相量图