欧氏空间内给定Gauss曲率的凸闭超曲面的存在性定理

设M是Rn＋1（正整数n≥2）内一光滑闭（即可定向连通紧致无边界）严格凸（即处处具有正的截面曲率）的超曲面，hij表示M沿Rn＋1内单位内法向量n的第二基本形式分量．〈，〉表示Rn＋1的内积．用表示M的局部正交标架场，表示其对偶基．可以知道M的第一、第二基本形式

M的Gauss映射φ：M→Sn（1），

由于〈n，n〉＝1，则〈n，dn〉＝0，因此可以写－dn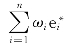＝，比较此公式与（3．2．2），有

〈dn，dn〉即是M的第三基本形式Ⅲ，又是Gauss映射φ的第一基本形式．利用公式（3．2．2）和（3．2．4），有

M的体积元素

对应的Gauss映射像的体积元素

这里利用了行列式按行的展开式及公式（3．2．6）．

由于超曲面M是严格凸的，det hij是实对称矩阵（hij）的所有正的特征根的乘积，因而处处大于零，从而Gauss映射的局部Jacobi矩阵处处非退化，这表明Gauss映射φ是一个浸入．在正交标架下，M的第二基本形式张量矩阵的特征根的乘积称为M的Gauss-Kronecker曲率，简称为Gauss曲率．

利用伍鸿熙等教授编著的《黎曼几何初步》一书中§5的引理9（［1］）可以知道，φ是一个覆盖映射，又由于Sn（1）（n≥2）是单连通的，利用拓扑学中的覆盖空间理论可知，φ是一个整体微分同胚．

如果Sn（1）在Rn＋1内的位置向量场r＝（x1，x2，…，xn＋1），Minkowski证明了下述公式：

这里K是M的Gauss-Kronecker曲率．由于Gauss映射是一个微分同胚，K可视为Sn（1）上一个正的可微分函数．公式（3．2．8）的证明后文会附带给出．

更有意义的是其逆问题：

K是Sn（1）上定义的一个正的Ck，α函数，这里正整数k≥3，α∈（0，1），如果满足上述公式（3．2．8）（注意K即K（r）），问是否存在Rn＋1内一个严格凸的闭超曲面M，使得M的Gauss-Kronecker曲率在Gauss映射下恰由K确定？历史上称其为Minkowski问题．

在Rn＋1内，给定一个严格凸的闭超曲面，对于Sn（1）上一点r＝（x1，x2，…，xn＋1），这里向量的起点始终在原点（Sn（1）的球心），r的终点是（x1，x2，…，＝1．为叙述方便，不区分向量及向量的终点，那么在M上有唯一点Y＝（y1，y2，…，yn＋1），由公式（3．2．3），有

这里r（Y）是M在点Y的单位外法向量，Y＝φ－1（r）．

下面定义Sn（1）上一个光滑函数，称为M的支持函数．令

显然，函数H*是H的延拓，记

这里利用了

上式最后一个等号是由于是M在向量Y的终点处的单位法向量．

因此，在Rn＋1内，M的位置向量场

在Sn（1）⊂Rn＋1－｛O｝内取局部正交标架场e1，e2，…，en，en＋1，使得e1，e2，…，en切于Sn（1），en＋1＝r．由公式（3．2．16）可以知道，Y等于函数H*（X）的梯度向量，从而有

这里下标B（1≤B≤n＋1）表示沿eB方向的导数．

利用

以及公式（3．2．16）和（3．2．17），有

这里最后一个等式利用了公式（3．2．10）以及＝r．利用公式（3．2．17）和（3．2．19），以及Y只依赖＝r，在公式（3．2．17）中，取|X|＝1，利用H*是H的延拓，有

上式两端在Sn（1）上微分，利用Rn＋1内Sn（1）的Gauss公式和Weingarten公式，有

在Rn＋1内，沿M的单位内法向量－r，M的第二基本形式分量hij可由下式确定：

这里利用〈r，Yj〉＝0，两端微分，导出

这里再一次利用了〈r，Yk〉＝0，1≤k≤n．利用（3．2．24），导出（3．2．23）的最后一个等式．由公式（3．2．22）和（3．2．23），有

利用公式（3．2．22），M的度量张量

这里i，j∈｛1，2，…，n｝．

而M在向量Y的终点处（向量起点始终在原点）的Gauss-Kronecker曲率

这里利用了公式（3．2．25）和（3．2．26），并且考虑到λ的n次方程det（hij－λgij）＝0的n个实根的乘积是K，故有公式（3．2．27）的第一个等式．

由上式，有

反之，如果能够找到一个Sn（1）上的可微正函数H，使得对称矩阵（Hij＋Hδij）是正定的，且满足公式（3．2．28），那么，从函数H出发，可以定义一个闭超曲面M，其位置向量场由公式（3．2．20）确定．有了公式（3．2．20），公式（3．2．21）—（3．2．28）成立．由于对称矩阵（Hij＋Hδij）是正定的，M是严格凸超曲面．

下面解Sn（1）上的方程（3．2．28），利用连续法，令

这里t∈［0，1］．由于K处处大于零，可以知道Kt是Sn（1）上一个正的函数，并且满足

这里r＝（x1，x2，…，xn＋1），并且利用了公式（3．2．8）．

令

这里正整数k≥3．正解的意思是解函数处处大于零．由于K0＝1，可令H0恒等于1，因此S是非空的集合．如果能证明：（1）S在［0，1］内是闭集；（2）S在［0，1］内是开集，利用闭区间［0，1］是连通的，则S就是整个闭区间［0，1］．令t＝1，则方程（3．2．28）是可解的．

先证明（1）．设｛tm|m∈N｝是S内一个序列，这里N是全体正整数组成的集合，它在［0，1］内收敛于一点t0．要证明t0∈S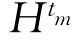，是定义在Sn（1）上的一列Ck＋2，α函数，满足

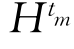对于每个tm，实对称矩阵都是正定的，且每个函数都是正的函数，即处处大于零．

对于每个函数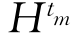，类似公式（3．2．20），定义

上式确定了Rn＋1内凸闭超曲面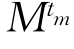，它的支持函数由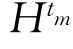给出，Gauss-Kronecker曲率是．

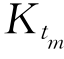接着，证明一些引理．

引理1　设M是Rn＋1内一个闭C4严格凸闭超曲面，K是Sn（1）上定义的M的Gauss-Kronecker曲率，那么，M的外部直径L满足下述不等式：

这里dA是Sn（1）在W处的面积元素（向量起点全在原点，这里不区分向量W与W的终点），Cn是仅与n有关的一个正常数．

证明　用d（x，y）表示两点x，y的连线段的距离，L＝由于M是紧致的，必在M上有两点p，q，使得

不失一般性，设Rn＋1的原点O是线段pq的中点．那么，在任何单位向量W∈Sn（1）处，M的支持函数

下面证明

这里W是固定的单位向量，且是点Y∈M处的单位外法向量（见公式（3．2．35））．

在Y*＝Y处，（利用Gauss公式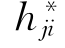）＝．由于M是严格凸闭超曲面，M沿单位外法向量W（即公式（3．2．3）中－n）的矩阵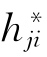（）是严格负定的，这里下标j*表示沿M的单位切向量的协变导数．实际上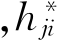，＝－hji．于是，在Y*＝Y处，f（Y*）有最大值．从而公式（3．2．36）成立．

顺便提及，因为与向量W垂直的M上点的切空间只有两个，即以W，－W为单位外法向量的M的点只有两点，垂直于向量W的M上的点切空间只有两个，一个是f的最大值点，一个是f的最小值点．

由于前面提及，Rn＋1内原点O是线段pq的中点，则

这里u是平行向量的单位向量．利用公式（3．2．36）可以知道，H（W）＞0，以及H（W）≥〈W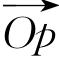，〉（由于点p∈M）．于是，再利用公式（3．2．39），有

由上式及K（W）是一个正的函数，立即有

这里dA是Sn（1）在向量W的终点处的面积元素（注意所有向量的起点都在原点）．由上式，可以得到

用dAM表示M的面积元素（也可以称为M的体积元素），利用公式（3．2．26）和（3．2．28），对凸闭超曲面M，M的度量gij的行列式，有

从而

利用上式，有

这里H＝H（W），只不过利用Gauss映射，函数H的定义域在M上．

在Rn＋1内，记X＝（x1，x2，…，xn＋1），可以知道

用M*表示闭超曲面M所包围的Rn＋1内区域，即M是M*的边界．利用Green公式，有

将上式代入公式（3．2．45），有

这里vol（M*）是M*的体积．

用A（M）表示闭超曲面M的面积（或称为M的体积），利用公式（3．2．44），有

很多人知道，在Rn＋1内，具有同一体积的区域，以球的表面积为最小．这导出下面Rn＋1内著名的等周不等式：

上式成立的理由是vol（M*）等于具有相同体积的实心球体D的体积，对于此实心球体D，应有

这里∂D是D的边界n维超球面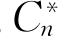，是仅与n有关的正常数．而A（∂D）≤A（M），因而有等周不等式（3．2．50）．

注：不等式（3．2．50）在一些专门叙述等周不等式的书籍中有证明．

将公式（3．2．48），（3．2．49）和（3．2．50）代入（3．2．42），可以看到

记Cn＝2（n＋1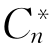），则引理1成立．

由引理1，以及可以知道，严格凸闭超曲面族Mtm的外部直径有一致的上界．只须将引理1中的M理解为Mtm，然后在不等式（3．2．52）两端取极限即可．

下面再证明一个引理．

引理2　在引理1中，一定能找到一个正常数r*，它只依赖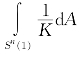的一个上界估计和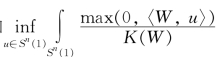dA的一个下界估计，使得在严格凸闭超曲面M的内部总能放入一个半径为r*的球．

证明　首先，寻找超曲面M在所有可能的超平面上的射影面积的一个下界．

设沿一个单位向量u，在垂直于u的一个超平面上，射影此超曲面M，那么以M为边界的区域M*的体积必小于M的外部直径L与射影面积A（Pu）之积，这是由于M*的体积必小于以A（Pu）为底面面积、以u方向为直母线方向的外切超柱面的体积．

利用公式（3．2．52）的第一个不等式，有

利用前面的叙述，有

将（3．2．54）代入（3．2．53），有

由于M*必落在以L为半径的闭球面内（利用（3．2．39）），则

从而L有一个正的一致的下界（将M换成Mtm，相对于凸闭超曲面族Mtm而言）．

因此，在M上能够找到两点P1和P2，它们之间的直线段距离有正的下界．

因为由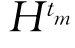的定义，参考公式（3．2．35）和（3．2．36），可以知道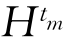≤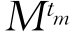的外部直径．接着在公式（3．2．36）中取Y*与r同方向，利用向量Y*的长度大于等于r*，导出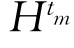（r）≥r*，从而不等式（3．2．58）成立．

注：公式（3．2．25）和（3．2．26）中向量W应改为这里的r．

下面证明

在Ω上定义一个函数：

这里i∈｛1，2，…，n｝．

由引理3的条件可以知道，是Rn内的有界闭集．可设φ在Ω内某点Q达到它的正的最大值（利用在Ω内，uii（x）＞0及（3．2．59）的第二式）．将公式（3．2．60）两端对xj求导，有

由于在Ω内部φ＞0，利用上式及公式（3．2．60），有

上式两端再对xj求导，有

在点Q，旋转坐标轴，使得当下标i≠j时，uij＝0．如果当矩阵（uij）对角化时，已证明引理3，则可以知道，对于非对角化正定矩阵（uij（x）），也必有引理3．

由于在点Q，φj＝0，利用公式（3．2．62），在点Q，有

用乘公式（3．2．63）的两端，并且关于j从1到n求和，那么，在点Q，有

由于在点Q，当下标j≠i时，uij＝0，那么在点Q，有

利用公式（3．2．64），在点Q，当下标i≠j时，有

利用上式，在点Q，有

将公式（3．2．66）和（3．2．68）代入公式（3．2．65），在点Q，有

在Ω内，方程det（ujk）＝F两端关于xi连续求导，用矩阵（ujk）表示矩阵（ujk）的逆矩阵，有

上式两端乘以uls，并且关于l从1到n求和，利用（3．2．73），有

在点Q，可以知道

将上式代入公式（3．2．70）和（3．2．75），在点Q，有

将公式（3．2．76）和（3．2．77）代入公式（3．2．72），在点Q，有

上式经过移项后，在点Q，可以看到

这里最后一个等式利用了公式（3．2．78）的中间等式．

公式（3．2．69）减去（3．2．79），且移项，利用（3．2．77）的第一式，在点Q，有

观察上式右端第一大项及最后三大项，在点Q，可以看到

上式最后一个等式右端的第二大项中只保留下标j＝i的项，然后将下标k改成j，恰与最后一大项抵消，从而可知最后的不等式．

将不等式（3．2．81）应用于公式（3．2．80），在点Q，有

由于uii＞0，在点Q，φjj≤0，再利用上式和（3．2．77）的第一式，在点Q，有

将上式两端乘以，并注意到公式（3．2．60），在点Q，可以得到

再利用公式（3．2．60），改写上式，在点Q，有

将上式左端视作含变元φ的首项系数是1的一元二次三项式，在点Q，立即有

这里β是一个正常数，由引理3中提及的量来估计．利用公式（3．2．60）的φ的定义，∀x∈Ω，有

这里αi是一个正常数，当然与β有关．

令

于是，引理3成立，这里α是一个正常数，依赖引理3中提及的量．

下面Ω是Rn内一个凸区域．

利用u是Ω上严格凸函数，而Ω又是Rn内一个凸区域，对于Ω内任何紧集Ω*，可设d（Ω*，∂Ω）＝a*，这里a*是一个正常数．设

不妨设x0∈Ω*，任取Ω*内不同于点x0的一点x，从点x0出发，用射线段连接点x0与x，交∂于点x*，u（x*）＝a．不妨旋转坐标轴，设从点x0到x*的方向是x1轴的正方向，于是可以写

这里为了简洁，就将点x*的第一分量写成x*（实数）等．由x1轴正方向的选择，有

利用（3．2．59）及上式，有

这里利用了d（x，∂）≤x*－x及d（x*，x0）＝x*－x0．

由于u是Ω内一个严格凸函数，沿着从点x0到x*的直线段，u的导数是严格单调增加的．利用一个初等不等式，当正数a，b，c，d满足时，明显地，有

利用Lagrange中值定理及上面叙述，可以知道

再利用上述初等不等式，立即有

化简上式左端，有

由不等式（3．2．92）和（3．2．95），有

于是，∀x∈Ω*（点x可以取点x0），由上式，有

这里d是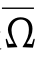的直径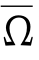（内任意不同两点直线段距离的最大值）．d≥d（x*，x0）．(www.chuimin.cn)

由上式，∀x∈Ω*，有

这里利用了d（x，∂）≥a*．

利用上述不等式于引理3，有

这里C是一个正常数．

下面证明：∀x∈Ω*，有

对于Ω*内任意一个固定点x＝（x1，x2，…，xn），旋转坐标轴，使得u的梯度向量方向就是x1轴的正方向．于是，有

利用（3．2．101），（3．2．103）和（3．2．104）于不等式（3．2．102）可以知道，不等式（3．2．100）成立．

注：不等式（3．2．100）不需要＝a这一条件．

下面来估计u的三阶导数．

将上式右端第四大项中的下标i与j互换，下标s与t互换，可以看到这一大项与上式右端第三大项相等．

将上式两端乘以，并且关于下标k，l，p，q，s，t全部从1到n求和．为书写简便，用∑表示对全部相同指标求和（除非有另外说明）．于是，可以得到

这里交换下标i与s*，j与t*，q与k，p与s，可以得到

类似地，交换下标i与s*，j与t*，l与k，s与t，可以得到

利用以上两式，可以看到（3．2．108）右端的最后三大项在乘以，且关于全部相同下标作和后，都是互相相等的，从而得到公式（3．2．109）．

令

将上式两端分别连续求导，且通过适当互换下标，有

在上式右端第三大项中互换下标s与t，j与k，可以看到这一大项等于上式右端第二大项．在上式右端第五大项中互换下标l与i，j与s，k与t，可以看到这一大项等于上式右端第四大项．在上式右端第七大项中互换下标i与j，l与s，可以看到这一大项等于上式右端第六大项．在上式右端第八大项中互换下标s与t，j与k，可以看到这一大项等于第七大项，也即等于第六大项．于是，利用上面叙述，公式（3．2．114）可简化为

将上式两端乘以upq，并且关于p，q求和（从1到n），再利用公式（3．2．75），可以看到

交换下标p，q，可以看到上式第一个等式右端的第三大项与第四大项相等．另外，交换下标j与s，k与t，i与l，a与b，可以看到上式第一个等式右端的最后一大项等于倒数第二大项，这一点下面将要用．

类似公式（3．2．63）后面的叙述，在任一固定点x∈Ω，作一个直角坐标轴的旋转，使得对称正定矩阵（uij）对角化．利用公式（3．2．109）和（3．2．116），注意这里的导数皆为普通导数，可以得到在点x处，

在上式右端第六大项中交换下标p与h，s与q，可以与上式右端第二大项合并．在上式右端第三大项中将下标p，q互换，另外将下标k换成l，l换成i，i换成k，与上式右端第五大项可合并．于是，在点x，有

利用公式（3．2．106），在点x，有

将公式（3．2．119）代入（3．2．118），在点x，有

注意公式（3．2．120）第一个等式右端的第四大项（即中括号内第二项乘相关项组成）与第五大项可合并，从而导出公式（3．2．120）．

观察公式（3．2．120）的右端第二大项与第三大项，可以得到

（将中括号内第二大项圆括号内第二项中的下标p，j互换，第三项中的下标k，p互换）

这里不等式右端第一大项等于B．将第二大项的下标s换成i，i换成l，l换成q，p换成h，j，k互换，可以看出这一大项恰等于A．将第三大项的下标j，k互换，恰等于A．将第四大项的下标k，i互换，也恰等于A．第五大项等于B．将第六大项的下标k，p互换，恰等于A．将第七大项的下标j，k互换，恰与第四项相等，等于A．将第八大项的下标j，k互换，恰与第六大项相等，也等于A．第九大项等于B．从而公式（3．2．123）最后一个等式成立．

由引理3，∀x∈Ω*⊂Ω，对于开区域Ω内任一点x，总有Ω内（与点x相关）紧集Ω*存在，使得x∈Ω*．有0＜uii（x）＜C，这里1≤i≤n．由于矩阵（uij（x））已对角化（当点x固定时），由方程det（uij（x））＝F（x）可导出

从而得到

这表明uii（x）有正的下确界．

利用公式（3．2．120）—（3．2．123），在点x，有

于是，∀x∈Ω*⊂Ω，利用不等式（3．2．125），可以看到

这里利用了公式（3．2．112）及对角化矩阵（uij（x））．

类似上式，有

公式（3．2．127）中C1与公式（3．2．128）中C2都是正常数．

利用（3．2．126），（3．2．127）和（3．2．128），在点x，有

这里C3＝C1＋C2，C4＝n3C1，C3，C4都是正常数．

下面证明

利用公式（3．2．121）和（3．2．131），有

这里将下标l换成k，k换成t，q换成s，h换成p，得上式第二个等式．

类似上式，利用公式（3．2．122）和（3．2．131），有

这里上式第二个等式右端第一大项等于B，第二大项等于A，第三大项等于－2A，第四大项等于A，第五大项等于B，第六大项等于－2A，第七大项等于－2A，第八大项等于－2A，第九大项等于4B，利用（3．2．134）的左端大于等于零，则（3．2．130）的第一个不等式成立．

利用（3．2．112），对于Ω内任一固定点x，对角化矩阵（uij（x）），再利用公式（3．2．131），有

利用（3．2．133），有

于是，（3．2．130）的第二个不等式成立．

利用（3．2．129）和（3．2．130），在点x，有

由于在点x，有

利用（3．2．137）和（3．2．138），在点x，有

这里C5＝C4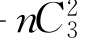＋，C5是一个正常数．

对于Ω内任何点y，固定这点y，为简便，不妨设是Rn的原点，设此原点离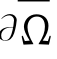的距离是正常数R．

令

又令

利用公式（3．2．140）和（3．2．141），在|x|≤R内，必有一点x*，使得f取最大值．显然有|x*|＜R，h（x*）＞0，在点x*，有

利用公式（3．2．141），有

利用公式（3．2．142）和（3．2．143），在点x*，兼顾公式（3．2．141），有

这里最后一个不等式利用了不等式（3．2．139）．

由上式，在点x*，可以看到

这里h的下标i表示h对xi的求导，且在点x*取值．将（3．2．148）代入（3．2．147），并且在此不等式两端乘以正数h2（x*），于是再利用公式（3．2．141），可以看到在点x*，有

整理上式左端，在点x*，有

由上式，立即有

这里C6是一个正常数．

利用（3．2．140）和（3．2．141），以及在点x*，f取最大值，再利用上式，有

注意原点O就是Ω内点y，由上式及公式（3．2．135）的第一个等式（将点x改为点y）、（3．2．125）的第二个不等式（将点x改为点y），有

这里C7也是一个正常数．

现在回到Minkowski问题的证明上来，先要建立一个普通直角坐标系与Sn（1）的局部正交标架公式之间的一些关系式，然后才能应用上述的一些结论．

在Rn＋1内，由于凸闭超曲面M的位置向量场满足公式（3．2．16），利用公式（3．2．9）前面的叙述，有＝1．在局部，不妨设xn＋1≠0，则

将（x1，x2，…，xn）作为Sn（1）的这个局部区域的坐标．

利用公式（3．2．9），沿超曲面M的单位内法向量－r，M的第二基本形式分量在普通直角坐标系下是下式（参考（3．2．23））：

将公式（3．2．159）和（3．2．160）代入（3．2．157）的第一个等式，利用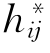依赖r，有

由于公式（3．2．160）的左端向量垂直于r，Y当然也依赖单位外法向量r，因而有

当X＝r＝（x1，x2，…，xn）时，可以将上式右端最后一项中的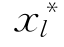改写为xl（1≤l≤n），所以，在普通直角坐标系下，当xn＋1≠0时，利用公式（3．2．165），M的Gauss-Kronecker曲率

由上式，有

由公式（3．2．11）和上式，上式左端中的H*完全可以被M的支持函数H代替．

将公式（3．2．170）的第二式代入（3．2．169），有

对于j∈｛1，2，…，n｝，有

利用（3．2．11）的第一个等式和（3．2．171），可以看到

由上式，有

这里上式最后一个等式是利用Green公式或Stokes公式，以及利用Sn（1）是无边界的流形．

下面要对公式（3．2．182）两端求导，先做些准备工作．利用行列式的求导法则，有

由上式，有

这里最后一个等式利用了（3．2．189）的第二式．

将上式代入公式（3．2．190），有

微分公式（3．2．182）的两端，有

如果上式成立，再利用公式（3．2．186），有公式（3．2．184）．

怎样才能既快又正确地证明（3．2．196）呢？由于公式（3．2．196）的左端关于j已作和，整体上是一个一阶张量，因而在Sn（1）的每一点上，只依赖单位切向量e1，…，en的选择，与局部坐标选择无关．因此，在Sn（1）的任意一个固定点上，取这点为中心的局部法坐标系．利用公式（3．2．193）和（3．2．195），在此固定点上，有

由上式，在此固定点上，有

在上式中，令p＝k，并且关于k从1到n求和，在此固定点上，有

利用Sn（1）上可微函数的Ricci恒等式，可以看到

利用公式（3．2．200）可以知道，公式（3．2．199）的右端是零．又利用det（Hst＋Hδst）＞0，可以知道，（3．2．196）在此固定点上成立．又由于此固定点是任选的，因而在整个Sn（1）上，公式（3．2．196）成立．从而公式（3．2．184）成立，这里利用了公式（3．2．186）．

现在证明：对于C5，α（Sn（1））内任何严格凸函数u，即矩阵（uij＋uδij）是正定的，有

这里r＝（x1，…，xn＋1）是Sn（1）⊂Rn＋1的位置向量场．

如果上述公式是成立的，那么，利用公式det（uij＋uδij）＝，有

这就是Minkowski公式的向量形式，u是Rn＋1内凸闭超曲面M的支持函数．

下面为方便，省略函数后面的自变量向量．

记

上式最后一个等式利用了公式（3．2．184）．

对于Sn（1）上的位置向量场r＝（x1，…，xn＋1），利用Sn（1）上的Gauss公式，有

这里B∈｛1，2，…，n＋1｝．

利用公式（3．2．183）和上式，有

从而有

Frechet导数具有与普通导数一样的性质，例如有

当t∈［0，1）时，上式右端矩阵是对称正定矩阵（利用矩阵（uij＋uδij）是对称正定的），在公式（3．2．210）左端用u＋tv代替u，这里v满足（3．2．215），有

再利用公式（3．2．203），（3．2．208），（3．2．211），（3．2．212），（3．2．215）和（3．2．218），有

从而公式（3．2．201）成立．

注：关于Frechet导数的知识可参考文章［2］的开始部分．

现在可以证明S是［0，1］内的开集了．

这里en＋1∧e1∧e2∧…∧en＝1，等式左端表示由e1，e2，…，en，en＋1张成的n＋1维单位立方体的体积．

由（3．2．226），有

而在Sn（1）上任意取定的一点正定矩阵（Hij＋Hδij）对角化时，可以看到矩阵（C（Hij＋Hδij））也是对角化正定矩阵，再利用公式（3．2．230），在这点上，有

利用公式组（3．2．241），兼顾公式（3．2．240），有

另外，可以知道det（Hst＋Hδst）＞0，利用公式（3．2．222），有〈X，en＋1〉＝H＞0，因而公式（3．2．238）左端的被积函数处处小于等于零．因此，公式（3．2．238）中被积函数处处等于零，从而在Sn（1）上处处有

这里后一个等式是利用公式（3．2．242），i，j∈｛1，2，…，n｝．利用公式（3．2．230）和矩阵（C（Hki＋Hδki））是可逆矩阵，有

利用公式（3．2．224）和上式，有

从而

Z是Rn＋1内一个常向量，这里aA（1≤A≤n＋1）全是实常数，利用公式（3．2．222）的第一式，有

引理5结论成立．

从前面的叙述可以知道，在H∈Ck＋2，α（Sn（1））时，由公式（3．2．221）定义的映射F（H）的Frechet导数是LH（u）（利用（3．2．183），（3．2．205）和（3．2．206）的相关部分），这里u∈Ck＋2，α（Sn（1）），正整数k≥3．对于固定正整数k，选择很大的正整数p，由Sobolev嵌入定理，在Sn（1）上具有直到p阶导数的Sobolev空间Hp（Sn（1））⊂Ck，α（Sn（1）），由公式（3．2．183）可以知道，LH是Sobolev空间Hp＋2（Sn（1））到Hp（Sn（1））内的自共轭算子．由引理5又可以知道，LH的核空间是Sn（1）上的线性函数空间，由标准的Hilbert空间理论可以知道，对于Hp（Sn（1））内满足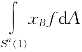＝0的函数f，这里（x1，x2，…，xn＋1）＝r是Sn（1）上的在Rn＋1内的位置向量场，必有一个解u∈Hp＋2（Sn（1）），满足LH（u）＝f（这里利用Fredholm二择一性质）．由于LH是一个自共轭算子，与LH的零空间正交的任一元素（例如f就具有这样的一个性质），必属于LH的值域空间，再利用线性椭圆型方程的正则性定理，有u∈Ck＋2，α（Sn（1））．于是LH是Ck＋2，α（Sn（1））到B*（参见（3．2．220））上的一个满的线性映射，从而F在H的Frechet导数LH是一个满映射．由非线性泛函分析理论可以知道，一定存在B*内包含的一个开邻域U，∀f∈U，方程

是可解的，这里u是Ck＋2，α（Sn（1））内一个正函数，而且矩阵（uij＋uδij）正定，所以S是开集，S＝［0，1］，这样，就得到了下述定理．

定理3（丘成桐和郑绍远）　设K是Ck，α（Sn（1））内一个正函数，这里正整数k≥3，α∈（0，1）．设对于Sn（1）上所有坐标函数xB（1≤B≤n＋1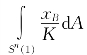），＝0，则能够解方程det（Hij＋Hδij）＝，这里解H∈Ck＋2，α（Sn（1）），并且能够在Rn＋1内找到一个闭凸超曲面，它的支持函数由H给出，它的Gauss-Kronecker曲率由K给定．

编者的话

1953年，Nirenberg解决了n＝2时的Minkowski问题（［3］），当然，同时代还有一些著名数学家用不同的方法解决了n＝2的Minkowski问题．1976年，丘成桐和郑绍远两位教授合作，解决了高维的Minkowski问题（［4］）．本讲主要内容就是利用他们合作的这篇文章编写的．

如果将本讲中的给定函数K推广到非负函数，是非常困难的．林长寿教授在1985年解决了局部Riemann流形到R3内的局部等距嵌入问题，此局部Riemann流形的度量导出的Gauss曲率除一点为零外，都是正的．他采用的方法主要是偏微分方程中的Nash-Moser迭代（［5］）．在林长寿教授工作的基础上，中国数学家们在局部Riemann流形到R3内的局部等距嵌入问题上有不少推广工作，有兴趣的读者可以阅读相关文章和专著．

参考文献

［1］伍鸿熙，沈纯理，虞言林．黎曼几何初步．北京大学出版社，1989．

［2］R．S．Hamilton．The inverse function theorem of Nash and Moser．Bull．Amer．Math．Soc．，New Series．7．1（1982）：65-222．

［3］L．Nirenberg．The Weyl and Minkowski problems in differential geometry in the large．Comm．Pure Appl．Math．，Vol．6（1953）：337-394．

［4］S．Y．Cheng and S．T．Yau．On the regularity of the solution of the n-dimensional Minkowski problem．Comm．Pure Appl．Math．，Vol．29（1976）：495-516．

［5］Chang Shou Lin．The local isometric embedding in R3 of 2-dimensional Riemannian manifolds with nonnegative curvature．J．Diff．Geom．，Vol．21（1985）：213-230．