【摘要】:,em,利用公式,由计算,可以看到同前面一样,这里下标j表示函数沿ej方向的协变导数.取正小数ε,令利用ε是正小数,以及0<k≤1,有0≤aε<1.利用公式,和,有由于M是闭流形,设F在M内某点x0达到最大值,则于是,利用,有在点x0,利用公式的第一式及,有上式两端乘以vj,且关于j也从1到m求和,在点x0,有利用公式的第二式、和,在点x0,有这里ω1,ω2,…,ωm是M上切向量e1,e2,…
设M是m维闭(紧致无边界连通可定向)Riemann流形,用Δ表示M上的Laplace算子,如果存在一个最小的正实数λ1,以及M上一个不恒等于零的光滑函数u,满足
则这个λ1称为M上Laplace算子的第一(正)特征值,u称为第一特征函数.由于M是闭流形,利用第1章内第3讲的引理3,有
这里dV是M上体积元素.由(2.5.2)的第二式可以知道,函数u有正有负.另外,由方程(2.5.1)可以看到,对于任一非零实数α,αu也是第一特征函数.因而可设
这里必要时可用-u代替u.
先证明一个引理.
引理1 如果M的Ricci曲率非负,则对于第一特征函数u,有
在M上选择局部正交标架场e1,e2,…,em,利用公式(2.5.4),由计算,可以看到
同前面一样,这里下标j表示函数沿ej方向的协变导数.取正小数ε,令
利用ε是正小数,以及0<k≤1,有0≤aε<1.
利用公式(2.5.6),(2.5.7)和(2.5.9),有
由于M是闭流形,设F(x)在M内某点x0达到最大值,则
于是,利用(2.5.14),有
在点x0,利用公式(2.5.15)的第一式及(2.5.16),有
上式两端乘以vj,且关于j也从1到m求和,在点x0,有
利用公式(2.5.15)的第二式、(2.5.16)和(2.5.17),在点x0,有
这里ω1,ω2,…,ωm是M上切向量e1,e2,…,em的对偶基,将公式(2.5.20)两端再外微分,有
上述公式称为Ricci恒等式.
注:为了降低阅读门槛,公式(2.5.20)—(2.5.25)是从最易懂的状态出发推导的,熟悉的读者可以略去部分或全部.
利用公式(2.5.22)和(2.5.25),可以看到
利用(2.5.14)和(2.5.33),以及F(x)在点x0取到最大值,有∀x∈M,
将上式两端乘以正数1-v2(x),有
利用公式(2.5.4),(2.5.5)和(2.5.9),有
利用aε∈[0,1),以及不等式(2.5.13),有
利用公式(2.5.11),有
利用公式(2.5.36),有
利用公式(2.5.36),有
利用不等式(2.5.35),∀x∈M,有
利用公式(2.5.36),有
由不等式(2.5.41)和公式(2.5.42),有
这就是引理1的结论.
记
d称为M的直径.这里d(x,y)是M上两点x,y的距离.
定理5(P.Li和丘成桐) 设M是m维闭Riemann流形,且M的Ricci曲率非负,则M上Laplace算子的第一(正)特征值
证明 利用公式(2.5.3),由于M是闭流形,存在M上两点x1,x2,使得
用一条极小测地线L连接上述两点x1,x2,则沿这条测地线L,利用不等式(2.5.43),有
利用不等式(2.5.46),有
这里ds>0.
由公式(2.5.48)和(2.5.49),有
将上式两端平方,有
利用公式(2.5.12),令
利用公式(2.5.12)和(2.5.52),有
于是,存在一个正小数δ,δ与ε有关,使得
利用公式(2.5.52),有
由(2.5.52)和上式,有
采用这种术语,利用公式(2.5.35),(2.5.37)和(2.5.57),有
利用不等式(2.5.51)可以看到,如果k=1,则由(2.5.5),有
下面设0<a<1,即0<k<1,令
利用不等式(2.5.59)、公式(2.5.61)及aε>0,有(www.chuimin.cn)
引理2 如果y(θ)是φ(θ)在θ0的闸函数,则
证明 利用(2.5.52),考虑函数
由公式(2.5.64)和(2.5.57),有
利用不等式(2.5.65)和上式可以知道,函数G(x)在x=x0处达到最大值.
由于M是一个闭流形,则
利用闸函数定义中的y(θ0)≥-1,以及利用公式(2.5.57)和(2.5.61),有
利用公式(2.5.55)的第一式,有
利用公式(2.5.10)和上式,有
由上式,再利用公式(2.5.52)和(2.5.54),有
将公式(2.5.64)两端微分,有
利用(2.5.69)的第一式及上式,在点x0,有
利用(2.5.69)的第二式及(2.5.74),在点x0,又有
这里θ=θ0(利用(2.5.66)的第一式).
利用Cauchy不等式,在点x0,有
利用公式(2.5.55)的第二式和上式,又利用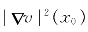 >0及cosθ>0,在点x0,有
>0及cosθ>0,在点x0,有
利用(2.5.26),(2.5.55),(2.5.73)和(2.5.78)于不等式(2.5.76),在点x0,有
这里利用公式(2.5.70),在点x0,可以看到
将公式(2.5.79)右端第一大项展开式中第二项的平方、右端第二大项、右端第三大项后一乘项中的第二大项、右端最后一大项中第一项合并运算,可以看到在点x0,有
上式右端第一项、第六项、第九项与第十二项的代数和恰为零.上式右端第二项、第五项与第十一项的代数和也是零.上式右端第三项、第七项和倒数第二项的代数和为-πsinθ.上式右端第四项、第十项可合并.上式右端第八项与最一项也可合并.
由于cos2θ>0,则引理3中的等式成立.至此,引理3的全部结论成立.
下面建立一个定理.
定理6(钟家庆和杨洪苍) 设M是无边界的紧致连通可定向的m维Riemann流形,且M的Ricci曲率非负,则M的Laplace算子的第一特征值λ1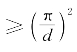 ,这里d是M的直径.
,这里d是M的直径.
证明 先证明
这里φ(θ)在公式(2.5.61)中确定,ψ(θ)在引理3中确定.
对不等式(2.5.102)用反证法,设此不等式不成立,则必存在θ0∈ ,使得
,使得
因此,当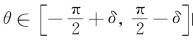 时,由上式,有
时,由上式,有
-1<ψ(θ0)+b=φ(θ0)(利用不等式(2.5.99)知此不等式成立),
因此,ψ(θ)+b是φ(θ)在θ0处的闸函数.利用引理2,应当有
不等式(2.5.105)与公式(2.5.104)的第二式是一对矛盾.因此不等式(2.5.102)成立.
利用公式(2.5.61)和(2.5.102),并注意到(2.5.11)中0≤aε<1,有
利用公式(2.5.57)和上式,有
由于M紧致,在M上存在x1,x2两点,使得
用一条极小测地线γ连接x1,x2两点,用s表示这条测地线的弧长参数,明显地,沿这条测地线,有
利用不等式(2.5.107)和(2.5.109),沿γ,有
这里ds>0.由于d是M的直径,则
这里L(γ)表示γ的长度.利用上式,有
令θ*=-θ,利用公式(2.5.97),有
利用公式(2.5.112)和(2.5.113)(将θ*改为θ),有
当实数x满足|x|<1时,显然有
将(2.5.115)代入(2.5.114),有
现在令ε→0,利用公式(2.5.53)和(2.5.54),伴随有δ→0,再由不等式(2.5.116),有
编者的话
本讲内容取自丘成桐和R.Schoen合著的《微分几何讲义》(第二版)第三章第109页至第117页([1]),当然,编者也查阅了钟、杨两位教授合作发表的文章([2]).算子特征值的下界估计是一个大的方向,有许多文献,有兴趣的读者可以去查阅相关文章及书籍.
参考文献
[1]丘成桐,孙理察.微分几何讲义.高等教育出版社,2004.
[2]钟家庆,杨洪苍.On the estimate of the first eigenvalue of a compact Riemannian manifold.中国科学(英文版),Vol.27(1984):1265-1275.


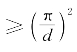 ,这里d是M的直径.
,这里d是M的直径. ,使得
,使得






相关推荐