本讲内容是上一讲定理的一个改进．先介绍一些引理．引理1设A1，A2是两个n×n实对称矩阵，已知Sj＝N，j＝1，2，以及S1＝S2，则证明由上一讲引理2，知上式两端都加上，则引理1成立．下面研究三个或三个以上n×n实对称矩阵A1，A2，…......
2023-11-23
Bernstein定理：微分几何进阶
【摘要】：设M是Rn＋1内一个完备连通可定向的（n维）稳定极小超曲面，M是否为超平面？这在历史上称为Bernstein猜测．本讲利用Cartan活动标架法及上一节引理2，来展开此问题的部分讨论．设M是Rn＋1内一个极小超曲面，在Rn＋1内选择一个局部正交标架场e1，e2，…，en＋1，使得限制于M，向量e1，e2，…，n｝．利用第1章第3讲的公式，注意C*＝0，p＝1，有S是Rn＋1内M的第二基本形式长度平方．在M的任意一点上，选择e1，e2，…
设M是Rn＋1内一个完备连通可定向的（n维）稳定极小超曲面，M是否为超平面？这在历史上称为Bernstein猜测．
本讲利用Cartan活动标架法及上一节引理2，来展开此问题的部分讨论．
设M是Rn＋1内一个极小超曲面，在Rn＋1内选择一个局部正交标架场e1，e2，…，en＋1，使得限制于M，向量e1，e2，…，en切于M，en＋1垂直于M．ω1，ω2，…，ωn＋1是对偶标架场，hij是M在Rn＋1内沿en＋1方向的第二基本形式分量．在本讲，下标i，j，k，l，s，…∈｛1，2，…，n｝．利用第1章第3讲的公式（1．3．23），注意C*＝0，p＝1，有
S是Rn＋1内M的第二基本形式长度平方．
在M的任意一点上，选择e1，e2，…，en，使得在这点上，当下标i≠j时，hij＝0．在这点上，有
由于M是极小超曲面，则
这里i∈｛1，2，…，n｝．
从而在M的这点上，利用公式（2．4．5）和（2．4．6），有
利用公式（2．4．3），（2．4．4）和（2．4．7），在M的这点上，有
上式中最后一个等式是由于
当M是非紧完备连通可定向Riemann流形时，如果上一讲公式（2．3．75）中的supp f是M内的一个紧致集时，公式（2．3．76）仍然是成立的．M上积分，实际上是在含supp f的M的一个紧致连通集合上积分．
在上一讲公式（2．3．76）中，用
f代替f，这里q是一个非负实数，f是M上一个非负光滑函数，那么，有
上式右端积分实际上是在S≠0的M的点集上进行计算．下面类似．
由于
对于M上任一光滑函数g，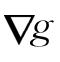
＝（g1，g2，…，gn）表示g的梯度向量，这里下标i表示沿ei的方向导数．
将公式（2．4．13）代入（2．4．12），有
用非负函数f2Sq乘不等式（2．4．10）的两端，有
在M上积分上式，有
利用supp f⊂M，有
由第1章第3讲的引理3的证明，或第2章第1讲的引理2可以知道第一等式成立．另外，取包含supp f的M内一个紧致连通区域D，上式两端实际上皆在D上积分，而在D的边界∂D，f恒等于零，利用Stokes公式可以知道，上式第二个等号成立．
而
将公式（2．4．21）代入（2．4．20）右端第二大项，可以看到
这里如果在M内一个连通开集上，f恒等于零，则
也恒等于零．积分区域中可删去这个连通开集；在剩余的M的一个零测集上，f等于零，积分时，删去这个零测集，不影响积分值．
利用不等式（2．4．33）和公式（2．3．34）于（2．4．36），有
由于ε1是任意一个正小数，利用（2．4．30）和（2．4．34），取ε1满足
将公式（2．4．38）代入（2．4．37），有(www.chuimin.cn)
由上式，有
用函数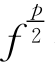
代替上述不等式两端中的f，有
β3是一个正常数，不等式（2．4．41）是一个重要的不等式．明显地，β3与函数f的选择无关，而且（2．4．41）的右端可以用在M上的积分来替代在M＋上的积分．
用BR表示M内半径为R的闭测地球，即
这里r是Rn＋1内点x（x∈M）到M上一个给定点O的距离函数．显然，有（注：r（x）也可以是M上给定点O的距离函数）
令
取θ为（0，1）内一个给定的正常数，令
显然F（r）是［0，∞］内一个连续函数．
将（2．4．45）（包含（2．4．46））代入（2．4．41），有
这里A（BR）是M内BR的n维面积（或称n维体积）．
如果
则不等式（2．4．47）的右端当R→∞时趋于零．由不等式（2．4．47）的左端可知M上S处处等于零，则M是全测地的，即M整体等距于Rn．
当n＜4＋
，即当n≤5时，可取p∈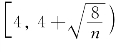
（见公式（2．4．24）前的叙述），使得
于是，有
定理4 （R．Schoen，L．Simon和丘成桐）设正整数n≤5，M是Rn＋1内稳定极小非紧完备连通可定向的n维超曲面，如果存在某个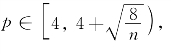
满足
＝0，这里A（BR）是Rn＋1内（或M内）以M上一固定点O为球心、半径为R的闭测地球的n维面积，则M是全测地的．
注：最后要说明一点，在本讲，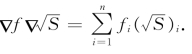
编者的话
限于本讲与上一讲合为一讲后篇幅较长，另外，上一讲内容本身又有很多其他应用，所以，思考后分成两讲，上一讲两个引理给出的两个著名公式实际是两个定理．
本讲内容取自R．Schoen，L．Simon和丘成桐三位教授于1975年合作发表的一篇文章（［1］）．
关于A（BR）的面积极限值公式（2．4．48），上述三位教授合作的文章有说明，有兴趣的读者可以看他们的文章．
几十年来，Bernstein猜测的延拓性研究在不断继续．例如，2005年，忻元龙教授发表的论文就值得一读，他研究了n＋p维欧氏空间Rn＋p内的稳定极小子流形的相关问题（［2］）．
［1］R．Schoen，L．Simon and S．T．Yau．Curvature estimates for minimal hypersurfaces．Acta Mathematics，Vol．134（1975）：275-287．
［2］Y．L．Xin．Bernstein type theorem without graphic condition．Asian J．Math．，Vol．9，No．1（2005）：32-44．
有关微分几何十六讲的文章
- 详细阅读
-
微分几何十六讲：子流形的基本方程详细阅读
，en＋p，即这里KABCD是N的曲率张量．本讲下标A，B，C，D，E，…，n＋p｝．可以知道定义曲率KBACD关于方向eE的协变导数KBACD，E如下：如果所有的KBACD，E都等于零，则Riemann流形N称为局部对称的Riemann流形．当时，这里C*是一个实常数，称N是具有常曲率C*的空间．请读者自己证明常曲率空间是局部对称的Riemann流形．在N内，选择一个局部正交标架场e1，e2，…，en，en＋1，…，en＋p，使得限制于M，向量e1，e2，…，n｝，α∈｛n＋1，…......
2023-11-23
-
微分几何第5讲：广义最大值原理详细阅读
我们知道，紧流形上的光滑函数有最大值．那么，对于完备Riemann流形呢？，en，沿测地线ρ，en＝，这里s是这测地线的弧长．M的互相垂直的单位切向量场e1，e2，…，en－1沿ρ是平行移动的．记是沿测地线ρ的Jacobi场，满足＝0，＝ei，这里为方便，沿测地线ρ的ei简记为ei．利用公式和，在r的可微分点，在r＞0的点及不在点P的割迹之内，r是光滑的（什么是割迹呢？......
2023-11-23
-
微分中值定理在武汉东湖学院论文集中的教学探索详细阅读
二、微分中值定理之间的关系通过以上分析证明，引导学生归纳总结得出三个微分中值定理之间有如下关系：Rolle中值定理 Lagrange中值定理 Cauchy中值定理。......
2023-12-04
-
瑟斯顿几何化定理三维空间局部形象图解详细阅读
我们可以用正十二面体来对三维双曲空间进行密铺。1982年，威廉·瑟斯顿首先提出将这种对应从二维推广到三维的几何化猜想。2003年，这个猜想最终被格里戈里·佩雷尔曼证实，这其实是他对庞加莱猜想证明的部分内容。几何意义上来讲，三维空间要比二维空间信息量更大。几何对应上，二维空间只有三种可能，而三维空间有八种。......
2023-11-22
-
用添加几何关系求解几何问题详细阅读
单击画直线命令，画直线的端点分别在AB、AC和BC上，同时利用智能尺寸标注AD=15mm，单击添加几何关系，按住Ctrl键选中AC和EF，从属性管理器中选中平行关系，如图1-38所示。单击画圆命令，以DF为直径画圆，然后再以F点为圆心，FE长为半径画圆，利用添加几何关系使刚才画的这两个圆相等，具体操作同上一步类似，如图1-39所示。......
2023-11-21
-
克里奇定理-《148个成功法则之克里奇定理》详细阅读
这句话后来被人称为：克里奇定理。另一只鹦鹉前则标道：此鹦鹉会四门语言，售价四百元。惠普公司在创建50周年之际，聘请专家在公司上下收集了100多个企业故事，其中“惠利特与门”流传最广。一天，董事长沃森违反了这条规定而被露西拦在安全区外，沃森的陪同人员表示不满，但沃森却取来了应该佩戴的标识。......
2023-12-01
-
函数微分的概念与定义详细阅读
【主要内容】1.函数微分的定义设函数y=f（x）在点x0的某个邻域内有定义.如果y在点x0处的增量Δy=f（x0+Δx）-f（x0） （其中，Δx是自变量x在点x0处的增量）可表示为Δy=AΔx+o（Δx）（其中，A与Δx无关，o（Δx）表示Δx→0时比Δx高阶的无穷小），则称y=f（x）在点x0处可微，称Δy的线性主部AΔx为y=f（x）在点x0处的微分，记为dy|x=x0（注意：函数y=f（x......
2023-10-27
相关推荐