首页理论教育极小子流形体积的变分公式

极小子流形体积的变分公式

2023-11-23 理论教育版权反馈

【摘要】：V（0）就是M的体积，可将V（t）视为Ft（M）的体积，因为当每个Ft都是整体等距嵌入时，V（t）的确是Ft（M）的体积．将公式（2．3．28）代入（2．3．25），有引理1（体积第一变分公式）因此，利用引理1，对任意的变分向量场W（x），体积的第一变分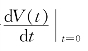等于零的充要条件是x∈M，H（x）恒等于零．引理1给出了极小子流形的一个几何解释．另外，可以知道公式（2．3．29）和（2．3．30）给出了W（

V（0）就是M的体积，可将V（t）视为Ft（M）的体积，因为当每个Ft都是整体等距嵌入时，V（t）的确是Ft（M）的体积．

将公式（2．3．28）代入（2．3．25），有

引理1　（体积第一变分公式）

因此，利用引理1，对任意的变分向量场W（x），体积的第一变分 pagenumber_ebook=158,pagenumber_book=150 等于零的充要条件是∀x∈M，H（x）恒等于零．引理1给出了极小子流形的一个几何解释．

另外，可以知道

公式（2．3．29）和（2．3．30）给出了W（x）的一个几何解释．

下面叙述体积的第二变分公式．

N内浸入子流形Ft（M）的平均曲率向量

当∂M＝Ø（空集），或Ft（∂M）＝F（∂M）（这里∀t∈（－ε，ε）），将公式（2．3．31）和（2．3．32）应用于公式（2．3．23），有

当F（M）是N内等距浸入极小子流形时，上式两端再对t求导一次，利用H（x，0）恒等于零，有

这里利用公式（2．3．11）和（2．3．12）后面的叙述，很容易得到上式左、右两端相等．

利用公式（2．3．12），（2．3．6），（2．3．9）以及用dM表示M的外微分，再兼顾公式（2．3．39），有

这里dA的意义见公式（2．3．25）后面的叙述．

下面来计算公式（2．3．38）的右端的第一大项．用KABCD表示N的曲率张量，限制于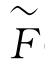 pagenumber_ebook=161,pagenumber_book=153 （M×（－ε，ε）），利用Cartan结构方程，有

上式第二等式右端的第一大项、第四大项和第七大项之和恰等于第三等式右端的第一大项．

利用公式（2．3．8）的第二式，有

Kαk（x）也是N内点F（x）由eα（x），ek（x）张成的Ricci曲率，这里局部叠合M与F（M），往往以ek（x），eα（x）依次代替ek（F（x）），eα（F（x））等．(www.chuimin.cn)

利用上述①—④和公式（2．3．51），有

当F（M）变分向量场是F（M）的法向量场时，利用公式（2．3．44）和（2．3．65），有

将公式（2．3．64），（2．3．65），（2．3．67）和（2．3．68）代入公式（2．3．57），有

将公式（2．3．69）代入公式（2．3．36），有

由于Ft（∂M）＝F（∂M），因此，∀x∈∂M，ωα（x，t）的表达式中不含变元t，再由公式（2．3．7）的说明，有∀x∈∂M，

由（2．3．73）知道，公式（2．3．72）的最后一个等式成立．

记aα，j（x）＝aα，j（x，0），利用（2．3．71）和（2．3．72），有

将公式（2．3．74）代入（2．3．70），有

引理2　（极小子流形的体积的第二变分公式）

设F（M）是n＋p维Riemann流形N内的n维极小带边界的紧致连通可定向（局部）等距浸入子流形，且F（M）的变分向量场是（保持边界不动的）法向量场，则

引理2有广泛的应用．

F（M）的变分向量场是保持边界不动的，即Ft（∂M）＝F（∂M），∀t∈（－ε，ε），如果又是F（M）的法向量场，则称为正常变分向量场．又为了方便，常常以M代替F（M）．例如，在n＋1维欧氏空间Rn＋1内，设M是在保持边界不动的正常变分条件下的稳定极小超曲面，则

这里f是满足supp f⊂M的C3（M）中函数，supp f表示集合｛x∈M|f（x）≠0｝的闭包．又＝0，由引理2，有

这里利用了公式（2．3．3）的第二式、（2．3．59）和（2．3．75）．另外，S（x）是Rn＋1内M在点x的第二基本形式长度平方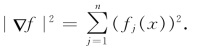． pagenumber_ebook=169,pagenumber_book=161

编者的话

这一讲是编者参考了几种教材后，用活动标架法仔细推导写成的．下一讲将介绍本讲引理2的一个著名应用．