欧氏空间内带边界的极小曲面的等周不等式

2023-11-23 理论教育版权反馈

【摘要】：下述平面上简单光滑闭曲线的等周不等式是众所周知的：这里M是平面内一区域，M的边界M是一条简单光滑闭曲线．A是M的面积，L是M的长度．本讲考虑n维欧氏空间Rn内极小曲面的情况．定义Rn内一个二维曲面M的边界曲线M称为弱连通的，如果存在Rn内一个直角坐标系｛x1，x2，…

下述平面上简单光滑闭曲线的等周不等式是众所周知的：

这里M是平面内一区域，M的边界∂M是一条简单光滑闭曲线．A（M）是M的面积，L（∂M）是∂M的长度．

本讲考虑n维欧氏空间Rn内极小曲面的情况．

定义　Rn（正整数n≥3）内一个二维曲面M的边界曲线∂M称为弱连通的，如果存在Rn内一个直角坐标系｛x1，x2，…，xn｝，使得对Rn内由方程xα＝常数确定的每个超平面Hα（这里α∈｛1，2，…，n｝），Hα不能分离∂M，即如果Hα∩∂M是空集，则∂M必位于Hα的一侧．

下面证明一个定理．

定理3（P．Li，R．Schoen and S．T．Yau）　设M是Rn（n≥3）内一个紧致带边界的二维极小曲面，如果M的边界曲线∂M是弱连通的，那么，（L（∂M））2≥4πA（M）．等号成立当且仅当M是Rn内某个平面内一个圆盘．

证明　分两步证明．首先考虑曲线∂M是连通的情况来证明这一等周不等式．通过一个平移，可设∂M的质量中心在Rn的原点．这里质量中心

s是∂M的弧长．

由于∂M是连通的，Rn内任何直角坐标系（x1，x2，…，xn）都满足弱连通的定义．

记X＝（x1，x2，…，xn），用〈，〉表示Rn的内积，用Δ表示曲面M的Laplace算子．明显地，有

取Rn的局部正交标架场e1，e2，…，en，使得限制于M，e1，e2是切于M的；限制于边界∂M，e1是M的边界∂M的单位外法向量．

在M上积分上式，有

这里要说明，在第1章第3讲引理3的证明中，如果紧致n维Riemann流形M有光滑边界∂M，利用公式（1．3．67）和（1．3．70），又利用Stokes公式，有

这里e1是∂M的单位外法向量，限制在∂M上，ω1＝0．有时，用en表示∂M的单位外法向量，这时∂M的诱导定向体积元素dA＝（－1）n－1ω1∧ω2∧…∧ωn－1，限制在∂M上，ωn＝0，得到同一结果，这一点读者要注意．另外，利用本章上一讲引理2，读者可以自己证明同一公式．在公式（2．2．6）中，令f＝〈X，X〉，由（2．2．6）能推出公式（2．2．5）的后一个等式．

利用（2．2．5），有

利用公式（2．2．3）的第一式，在∂M上两端积分，有

这里s是曲线∂M的弧长．

由于∂M的质量中心在原点，利用（2．2．2），有

利用上式及Fourier级数理论，有

这里k∈｛1，2，…，n｝．

利用上式，有

将上式两端平方，且在∂M上积分，利用三角级数的性质，可以得到

利用公式（2．2．10）及三角函数的周期性，两端平方后再在∂M上积分，有

由（2．2．15）和（2．2．16），有

改写上式，可以看到

不等式（2．2．18）称为Poincarè不等式．

利用s是曲线∂M的弧长，有

将不等式（2．2．18）两端关于下标k从1到n求和，利用（2．2．19），有

将公式（2．2．8）和（2．2．20）代入（2．2．7），有

由上式，有等周不等式

当不等式（2．2．22）取等号时，前面的一切不等式都取等号．特别利用不等式（2．2．7）取等号，在∂M上处处有

这里R是一个正常数．又不等式（2．2．15）取等号，有

将上式代入公式（2．2．10），有

为简便，下面用ak代替常数ak1，bk代替常数bk1．通过直角坐标系的旋转，可以使得

利用上式，有

又利用公式（2．2．25），有

比较公式（2．2．26），（2．2．28）和（2．2．29），有(www.chuimin.cn)

利用公式（2．2．25），（2．2．30）和（2．2．31），有

利用公式（2．2．23），在∂M上，处处有〈X（s），X（s）〉＝R2，兼顾公式（2．2．32），有

利用公式（2．2．32）和（2．2．33），在∂M上，有

∂M是x1x2平面内以原点为圆心、半径为R的圆周．由公式（2．2．3）的第二式，有

利用公式（2．2．34），在下标k≥3时，在∂M上函数xk恒等于零．

下面来推导一个以后经常要用的公式．

设f，g是M上两个光滑函数，这里M是一个n维连通可定向的带边界（或不带边界）的Riemann流形．设e1，e2，…，en是M的局部正交标架场，ω1，ω2，…，ωn是其对偶基．明显地，有

这里fk是f沿ek的方向导数，gk是g沿ek的方向导数．

令

利用第1章第1讲的编者的话中的公式（1．1．56）—（1．1．60），读者很容易证明X是M上的整体定义的光滑向量场．

利用第2章第1讲内公式（2．1．13）和（2．2．37），有

这里*是M上的Hodge算子（见本章第1讲内公式（2．1．60））．

利用本章第1讲内公式（2．1．14）及上式，有

利用本章第1讲内引理2建立的Green公式，设n＝e1是∂M的单位外法向量，由公式（2．2．39），有

这里习惯上将f沿∂M的单位外法向量n的方向导数记为fn．

特别，当f＝g＝xk时（这里固定下标k≥3），由于在∂M上，xk＝0，利用公式（2．3．40），有

由公式（2．2．35），上式左端第一项积分为零，则上式左端第二项被积函数在M上处处为零，因而在M上xk为常值，由于xk在∂M上为零，则xk在M上处处为零．

注：当M是闭流形时，公式（2．3．40）的右端用零代替．当然，熟悉偏微分方程的椭圆型方程理论的读者可以利用经典的最大值原理知道，M内函数xk的最大值与最小值都在∂M上达到，从而也可以得到同一结论．

由于当下标k≥3时，xk恒等于零，则曲面M必在x1x2平面内．曲面M就是x1x2平面内一个以原点为圆心、半径为R的圆盘（注意公式（2．2．34））．这时，L（∂M）＝2πR，A（M）＝πR2，等周不等式（2．2．22）取等号．由此，当∂M是连通曲线时，定理3结论成立．

当∂M是弱连通时（当然设∂M不连通），记

这里σk是一条连通的闭曲线，类似连通情况，将∂M的质量中心平移到原点．可以选择一个适当的直角坐标系｛x1，x2，…，xn｝，满足下述性质：对于任何固定α∈｛1，2，…，n｝，存在平移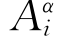 pagenumber_ebook=149,pagenumber_book=141 ，i∈｛2，3，…，p｝，此平移由垂直于的向量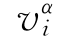生成，使得平移曲线｛｜i＝2，3，…，p｝与σ1组成一个连通集．

下面对正整数p（p≥2）用数学归纳法来证明上述的结论．

当p＝2时，因为存在一个直角坐标系｛x1，x2，…，xn｝，没有形式xα＝常数（1≤α≤n）的超平面能分离σ1，σ2．那么，存在一个实数x，使得由方程xα＝x确定的超平面H必与σ1和σ2都相交．记q1，q2分别是超平面H与σ1和σ2的交点．明显地，能够沿着此超平面平移点q2到q1，用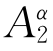 pagenumber_ebook=149,pagenumber_book=141 表示这个平移，这个平移垂直于此平面的单位法向量，并且是连通的．

设上述结论对p－1成立，这里某个正整数p≥3．对于正整数p，考虑由下述数

组成的集合｛y1，y2，…，yp｝，这里α是｛1，2，…，n｝内一个固定元素，s是连通闭曲线σi的弧长（当i固定时）．

不失一般性，可以假设

利用公式（2．2．47）和（2．2．48），有

利用Poincarè不等式，有

将上式关于α从1到n求和，利用公式（2．2．42），有

在∂M是弱连通且不连通时，即在情况（2．2．42）时，公式（2．2．7）和（2．2．8）还是成立的，于是，有

由上式，立即有不等式（2．2．22）．如果在∂M是弱连通情况（2．2．42）时，不等式（2．2．22）取等号，那么，不等式（2．2．50）—（2．2．52）都取等号．特别不等式（2．2．7）取等号．要注意不等式（2．2．51）与不等式（2．2．20）是一样的，只是下标k换成了α．用连通闭曲线σα代替∂M，在∂M连通时的等号成立情况几乎可以原封不动地搬到σα上．因此，在每个σα上，通过一个直角坐标系的旋转，成立公式（2．2．34）．即由一个直角坐标系的旋转后，连通闭曲线σ1为x1x2平面上以原点为中心、半径为R的圆周．即σα叠合于圆周σ1．对于σα内每个圆周（i＝2，3，…，p）及σ1，有

由于不等式（2．2．51）取等号，利用L（∂M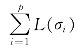）＝ pagenumber_ebook=152,pagenumber_book=144 及上式，立即有p＝1（用反证法，如果p≥2，不等式（2．2．51）必取严格不等号）．

编者的话

本讲内容是根据P．Li，R．Schoen和丘成桐教授1984年合作的一篇文章写成的．

参考文献

［1］P．Li，R．Schoen and S．T．Yau．On the isoperimetric inequality for minimal surfaces．Ann．Scuola，Norm．Sup．Pisa．，Vol．11（1984）：237-244．

欧氏空间内带边界的极小曲面的等周不等式

相关推荐