4维球面内闭曲面长度平方的定理

2023-11-23 理论教育版权反馈

【摘要】：在本讲，p＝1，简记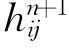为hij，利用第3讲内公式（1．3．20），可以看到在n＋1维常曲率C*的空间内，对于n维超曲面M，在本讲，M的平均曲率H和数量曲率R都是常数，利用上式，M的第二基本形式长度平方S也是常数．在这些条件下，公式（1．6．1）可简化为下述公式：利用第1讲内公式（1．1．10）和（1．1．33），即利用（1．3．34），（1．1．43），（1．1．47），有这里hijkl的沿es方向

在本讲，p＝1，简记 pagenumber_ebook=86,pagenumber_book=78 为hij，利用第3讲内公式（1．3．20），可以看到在n＋1维常曲率C*的空间内，对于n维超曲面M，

在本讲，M的平均曲率H和数量曲率R都是常数，利用上式，M的第二基本形式长度平方S也是常数．在这些条件下，公式（1．6．1）可简化为下述公式：

利用第1讲内公式（1．1．10）和（1．1．33），即利用（1．3．34），（1．1．43），（1．1．47），有

这里hijkl的沿es方向的协变导数hijkls定义如下：

利用（1．6．6）的第一式以及（1．6．7），很容易推导出（1．6．6）的第二式．

利用第1讲内公式（1．1．40），有

同前几讲一样，仍用Δ表示M上的Laplace算子．

利用（1．6．3）和（1．6．8），有

利用第1讲内公式（1．1．36），有

上式两端外微分，有

利用第1讲内公式（1．1．17），（1．1．20），以及本讲公式（1．6．7），（1．6．11）和（1．6．12），有

上式右端（去括号后）一共有18大项．将上式右端第一大项中的下标l与s互换，恰与左端第二大项相等．将上式右端第七大项中的下标l与s互换，恰与左端第三大项相等．将上式右端倒数第六大项中的下标l与s互换，恰与左端第四大项相等．将上式左端最后一大项中的下标l与s互换，恰与左端倒数第二大项之和为零．将上式右端第五大项的下标l与s互换，恰与右端第二大项之和为零．将上式右端第八大项的下标l与s互换，恰与右端第三大项之和为零．将上式右端倒数第五大项中的下标l与s互换，恰与右端第四大项之和为零．将上式右端倒数第八大项中的下标l与s互换，恰与右端第九大项之和为零．将上式右端倒数第四大项中的下标l与s互换，恰与上式右端第十大项之和是零．将上式右端倒数第二大项中的下标l与s互换，恰与右端倒数第三大项之和是零．

利用上述的化简，公式（1．6．13）可简化为下述公式：

将上式右端下标反称化后，有

利用（1．6．14）和（1．6．15），可以看到这两公式右端应相等．将公式（1．6．14）右端中的三大项下标l与t互换，可以得到

上式右端两大项恰是公式（1．6．20）右端中第二大项与倒数第四大项．

公式（1．6．18）的右端第三大项与倒数第三大项之差

上式右端两大项恰是公式（1．6．20）右端中第五大项与倒数第六大项．

公式（1．6．18）右端的第四大项与倒数第一大项之差

上式右端两大项恰是公式（1．6．20）右端中第七大项与倒数第二大项．

公式（1．6．18）的右端第五大项与倒数第二大项之差

上式右端两大项恰是（1．6．20）右端第八大项与倒数第一大项．另外，将（1．6．20）右端第三大项的下标s与t互换，与（1．6．20）右端第六大项之和恰是零．将（1．6．20）右端第十大项的下标s与t互换，与（1．6．20）右端第三大项之和恰是零．

利用（1．6．17），（1．6．18），（1．6．20）—（1．6．24）及上述叙述，有

这里（1．6．20）右端剩余四大项中交换了下标s与t．

由（1．6．25），有

将（1．6．28）代入（1．6．27），再利用（1．6．2）的第一式，有

将公式（1．6．36）左端第三大项减去（1．6．36）右端第五大项，加上（1．6．36）倒数第四大项，有

将公式（1．6．36）左端第四大项减去（1．6．36）右端第六大项，加上（1．6．36）倒数第四大项，有

将公式（1．6．36）左端第五大项减去（1．6．36）右端第三大项，加上（1．6．36）最后一大项，有

注意到上述公式（1．6．37）—（1．6．40）右端之和恰为零，应用公式（1．6．37）—（1．6．40）于公式（1．6．36），可以得到

下面来计算公式（1．6．34）的右端各大项．

上式右端第二大项与第五大项可合并，上式右端第三大项与第十大项可合并（交换第十大项的下标i与j），上式右端第四大项与第十一大项可合并（交换第十一大项的下标i与j，t与l）．利用Codazzi方程组，也可以将上式右端倒数第三大项、倒数第四大项和倒数第六大项合并，上式右端第七大项、第十二大项和第十四大项可合并，上式右端第八大项与倒数第一大项可合并．

经过这些合并后，公式（1．6．46）可简化为

当M的平均曲率H和数量曲率R都为常数时，这时S也必为常数．于是公式（1．6．47）可简化为下述公式：

将上述公式（1．6．50）—（1．6．52）代入（1．6．49），并注意到（1．6．51）的右端第一大项与（1．6．52）右端第一大项可合并，也可以与（1．6．52）右端最后一大项合并起来，（1．6．51）右端最后一大项与（1．6．52）右端第三大项代数和是零，则（1．6．49）可简化为下述公式：

对张量求导不熟悉的读者，可作为一个习题去证明（1．6．56）和（1．6．57）两个左端应相等．

利用（1．6．48），（1．6．53）和（1．6．57），注意H，S都是常数，有

这里上式右端第二大项与最后一大项能合并（交换最后一大项的下标l与k，i与j，并且利用Codazzi方程组）．

可以看到

将（1．6．60）代入（1．6．59），当H为常数时，有

下面分两种情况讨论．

本讲只考虑4维单位球面S4（1）内3维闭极小（等距浸入）超曲面M．换句话讲，下面C*＝1，n＝3，H恒等于零．

首先，公式（1．6．60）可简化为

由于本讲S也是常数，公式（1．6．55）简化为

在M的任意一点处，选择e1，e2，e3，使得当i≠j时，hij＝0，这里记hii＝λi，则

将上面第一式两端平方，有

将上式两端再次平方，利用（1．6．67）的第一式，有

将（1．6．67）的第二式两端平方，再利用上式，有

于是，在M的任意一点处(www.chuimin.cn)

这表明上式左端在M上是常数．

利用公式（1．6．65）和上式，有

改写公式（1．6．66），并且利用上式，可以得到

利用Codazzi方程组，可以看到在M的任意一点处，有

由（1．6．73）和（1．6．74），有

由（1．6．76）和（1．6．77），有

将上述n个等式关于下标从1到n求和，利用引理条件，有

将（1．6．79）代入（1．6．78），有

于是，aj只有两个值

可设s个aj取正值a，n－s个aj取负值b．由引理的两个条件，有

解上述方程组，得

当s＝1时，上式右端达到最大值．当s＝n－1时，上式右端达到最小值．于是，有

引理1的结论成立．

利用（1．6．67）和引理1，有

即

不妨设λ1≤λ2≤λ3．不等式（1．6．87）的右端取等号，必有λ1＝λ2＜λ3；不等式（1．6．87）的左端取等号，必有λ1＜λ2＝λ3．这里，由公式（1．6．67）可知，λ1，λ2，λ3都是常值．

下面的一个引理是很关键的．

利用公式（1．6．49）的推导过程及上式，在点q，有

利用hjk＝λkδjk及上式，在点q，有

在点q，选择e1，e2，e3，使得hij＝λiδij，则上式的第二式变为

由（1．6．93）的第一式，（1．6．94）和（1．6．92）组成的方程组的系数行列式

注意，在点q，上式右端不等于零．因此，在点q，必有

这里利用了当i，j，k两两不相等时，λi＋λj＋λk＝ pagenumber_ebook=105,pagenumber_book=97 ＝0．公式（1．6．97）和（1．6．98）是一对矛盾，因而引理2成立．

利用引理2，有

利用（1．6．67）和上式，不妨设λ1（q）＜λ2（q）＜λ3（q）．利用代数多项式理论，可以知道λ1（q），λ2（q），λ3（q）必是方程λ3－＝0的三个根．于是，有

利用（1．6．94）和（1．6．100），在点q，有

由（1．6．93）的第一式和上式，在点q，有

利用上式及Codazzi方程组，在点q，有

上式两端乘以12，并且因式分解左端，有

由于正常数S＞3，则上式左端第二个因式大于零，于是有

下面考虑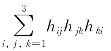 pagenumber_ebook=109,pagenumber_book=101 在M上等于常数的情况．

利用公式（1．6．67）的第一式、（1．6．68）和上述条件，由多项式理论，可以知道，特征值λ1，λ2，λ3是方程

的三个实根，这里A是一个常数，于是λ1，λ2，λ3全是常数．这样的3维超曲面称为常主曲率超曲面，也称为S4（1）内等参超曲面．类似地，Sn＋1（1）内常主曲率超曲面也称为等参超曲面．

由上面叙述，有

定理5（彭家贵、滕楚莲）　设M是S4（1）内3维闭极小超曲面，M在S4（1）内的第二基本形式长度平方S是一个大于3的常数，则

（1）S≥6；或者

（2）M是等参超曲面．

编者的话

本讲内容取自彭家贵、滕楚莲两位教授1983年合作发表的文章（［1］）．关于等参超曲面，奠基的工作是E．Cartan于1938年发表的一篇文章（［2］）．彭、滕两位先生在上述文章中证明了Sn＋1（1）内等参超曲面S只能取值0，n，2n，3n或5n．因此，在S4（1）内3维闭极小超曲面M，当S是常数且S＞3时，必有S≥6．这就是S4（1）内闭极小超曲面第二基本形式长度平方S的第二空隙性定理．在第3讲，陈省身等三位教授的结果历史上称为Sn＋1（1）内闭极小超曲面的S的第一空隙性定理．

1993年，Chang Shaoping将上述定理推广到S4（1）内极小超曲面片情况（［3］）．另外，将极小改为常平均曲率，Chang Shaoping研究了S4（1）内常平均曲率和常数量曲率闭超曲面M，证明了M必是等参超曲面（［4］）．

对于Sn＋1（1）内闭极小超曲面M，当M的第二基本形式长度平方S是大于n的常数时，较佳的估计是由杨洪苍与陈庆明合作，在1994年给出的，这两位教授证明了，当n较大时，S＞n＋（［5］）．最近，忻元龙教授与他的一位学生合作，得到了S是变量时的一个类似结果．有兴趣的读者可以去看他们的文章．很多同行都认为当常数S＞n时，应当有S≥2n．

另外，关于等参超曲面，有许多后续的工作，读者若有兴趣可以去查看相关的文献．

参考文献

［1］C．K．Peng and C．L．Terng．Minimal hypersurfaces of sphere with constant scalar curvature．Ann．of Math．Studies 103．Princeton University Press，1983：177-198．

［2］E．Cartan．Familles de surfaces isoparamétriques dans les espacesàcourbure constante．Annali di Mat．，17（1938）：177-191．

［3］Chang Shaoping．On minimal hypersurfaces with constant scalar curvatures in S4．J．Diff．Geom．，37（1993）：523-534．

［4］Chang Shaoping．A closed hypersurface with constant scalar and mean curvature in S4 is isoparametric．Comm．Anal．and Geom．，1．No．1（1993）：71-100．

［5］Yang hongcang and Cheng qingming．An estimate of the pinching constant of minimal hypersurfaces with constant scalar curvature in the unit sphere．Manuscripta Math．，84．No．1（1994）：89-100．

4维球面内闭曲面长度平方的定理

相关推荐