球面内极小闭子流形长度平方的空隙性定理

当N是具有常曲率C*的空间时（见第1讲公式（1．1．10）），首先有

引理1　当N是具有常曲率C*的空间时，N必是局部对称空间．

证明　利用第1讲公式（1．1．10），有dKABCD＝0，再由第1讲的公式（1．1．9）及（1．1．10），有

公式（1．3．1）的右端第一项与（1．3．4）的右端第一项之和是零．公式（1．3．1）的右端第二项与（1．3．3）的右端第二项之和是零．公式（1．3．2）的右端第一项与（1．3．3）的右端第一项之和是零．公式（1．3．2）的右端第二项与（1．3．4）的右端第二项之和是零．

利用（1．3．1）—（1．3．4），以及以上叙述，兼顾第1讲内的公式（1．1．9），有

引理1的结论成立．

在N是具有常曲率C*的空间时，下面仔细计算第1讲内公式（1．1．51）的右端各大项．

将上述（1．3．6）—（1．3．12）的相关公式代入第1讲的公式（1．1．51），有

上式两端乘以，并且关于下标i，j从1到n求和，关于α从n＋1到n＋p求和，有

将公式（1．3．15）右端第五大项的下标l换成j，下标j换成k，下标k换成l，可以看到

将公式（1．3．15）右端最后一大项的下标i与k互换，有

将公式（1．3．15）右端倒数第二大项的下标j与k互换，有

公式（1．3．15）右端第五项的系数是2，公式（1．3．16）已经变形了其中的一半，对于另一半，将下标l与j互换，有

将上述公式（1．3．16）—（1．3．19）应用于公式（1．3．15），可以得到

公式（1．3．20）是一个很重要的公式．

特别地，当M是极小子流形时，在M上处处有

在本讲，下标表示及范围同第1讲．

由上式以及第1讲的公式（1．1．28）和（1．1．36），立即有

将（1．3．21）和（1．3．22）代入（1．3．20），有

公式（1．3．23）也是一个很重要的公式．

当N是n＋p维单位球面Sn＋p（1）时，C*＝1，记

这里α，β∈｛n＋1，…，n＋p｝．

又由第1讲公式（1．1．25）可以知道S．于是，公式（1．3．23）可以改写为

p×p矩阵（Sαβ）显然是一个实对称矩阵，在M的任意一点，利用线性代数知识知道，可选择en＋1，…，en＋p，使得当α≠β时，Sαβ＝0．这时记

对于一个n×n实矩阵A＝（aij），令N（A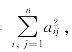）＝即N（A）＝trace（AAT），这里AT表示矩阵A的转置．N（A）是乘积矩阵AAT的追迹．显然，对任何n×n实正交矩阵T，有

记n×n实对称矩阵Hα＝（）（当α固定时），利用上面的叙述，公式（1．3．25）可简记为下述形式

下面证明一个引理．

引理2　设A，B是两个实对称n×n矩阵（正整数n≥2），则N（AB－BA）≤2N（A）N（B）．对于非零矩阵A和B，上式等号成立当且仅当存在一个实正交n×n矩阵T，满足

T－1 AT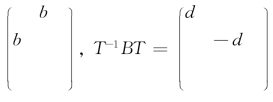＝（矩阵空白处皆为零，下同）．而且，如果A1，A2和A3是实对称的n×n矩阵，并且始终有N（AαAβ－AβAα）＝2N（Aα）N（Aβ），1≤α，β≤3，那么，其中至少有一个矩阵Aα是零矩阵．

证明　由于B为实对称n×n矩阵，利用线性代数知识可以知道，存在一个实n×n正交矩阵T，使得

现在假设A和B都是非零矩阵，而且满足

则（1．3．30）公式推导中等号处处成立．因而有

以及如果某些aik≠0，则对应有

由上式，有

由于A是非零矩阵，又由于（1．3．32），不失一般性，假设

从而有

由公式（1．3．30）的最后一个不等式取等号，又有

由上式，立即有

由于B不是零矩阵，由（1．3．29）的第一式，以及（1．3．36），有

当下标集合（i，k）≠集合（1，2）时，利用公式（1．3．30）的最后一个不等式取等号，以及（1．3．38），有

然而bi，bk中至少有一个是零（由于（1．3．38）），利用（1．3．36）和（1．3．39），有

再由（1．3．29），有

为了证明引理2的最后一个结论，用反证法，设A1，A2，A3全是非零实对称矩阵，利用上述证明，首先存在一个实n×n正交矩阵T，使得

利用（1．3．43）的第二式，以及（1．3．42），将矩阵B改为A2，矩阵A改为A3，应当有

公式（1．3．48）和（1．3．49）是一对矛盾．

利用上述引理，以及公式（1．3．28），有

由（1．3．57）知（1．3．59）和（1．3．60）的两个左端相等，因而这两公式的右端也应相等．另外，将（1．3．60）右端第四大项的下标α与β互换，与（1．3．60）的右端最后一大项之和是零．（1．3．59）的右端第二大项与（1．3．60）的右端倒数第二大项相等．由上述理由，可以看到

将上式右端的倒数第二大项的下标i与s互换，与右端的第二大项之和是零．将上式右端的倒数第一大项的下标j与s互换，与右端的第三大项之和是零．于是，可以看到

Δ表示M上的Laplace算子，则利用上式，可以得到

如果M是一个紧致连通无边界可定向的Riemann流形，则简称M是一个闭（Riemann）流形．设M是一个闭流形，f是M上任意一个光滑函数，有下述结论．

引理3　设M是一个闭（Riemann）流形，对于M上任意光滑函数f，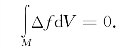

证明　设M是n维的，令

dV是M的体积元素．

从形式上看，由（1．3．67）定义的ω是局部的，下面证明它实际上是在M上整体定义的．换句话讲，要证明由（1．3．67）定义的ω不依赖局部坐标的选择．对于局部正交标架而言，要证明这个ω在保持流形定向时，不依赖局部正交标架的选择．

公式（1．3．78）表明ω是定向流形M上一个整体的n－1次形式．

由于M是闭流形，利用Stokes公式，有

利用（1．3．70）和（1．3．79），有引理3的结论．

利用（1．3．81）和（1．3．82），在M上处处有

由引理4条件S＞0及上式，知引理4结论成立．

现在来确定Sn＋p（1）内S恒等于正常值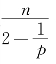的闭极小等距浸入子流形M．

利用（1．3．54）和（1．3．80）知，在M上处处有

由（1．3．84）的第二个等式，有(www.chuimin.cn)

由于不等式（1．3．50）也取等号，有

再由引理2知至多两个Hα矩阵是非零矩阵．

下面分别考虑p＝1和p≥2的情况．

①当p＝1时，简记hij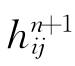＝，由（1．3．85），有hijk＝0，对于任意正整数S，可以看到

这里Cs是一个实常数．

在M内任意一点P，选择e1（P），…，en（P），使得当i≠j时，hij（P）＝0，即将实对称矩阵（hij（P））对角化．由于C1，C2，…，Cn都是与点P无关的实常数，利用代数中的多项式理论可以知道，特征值h11（P），h22（P），…，hnn（P）是首项系数为1的一元n次常系数多项式的n个实根，这些常系数是与P无关的实数．因此，特征值h11（P），h22（P），…，hnn（P）都是与点P无关的实数．利用特征值hjj（P）（1≤j≤n）对点P的连续性可以知道，在M内实对称矩阵（hij）的特征值都是实常数．对应的M的局部切向量场是光滑的（见［1］第232页至第234页）．对于常数对角矩阵（hij），有

引理5　存在正整数m＜n，在适当选择正交基e1，e2，…en后，有

（1）h11＝h22＝…＝hmm＝λ（λ为常数）；hm＋1，m＋1＝hm＋2，m＋2＝…＝hnn＝μ（μ是常数）；λμ＝－1；

（2）ωij＝0，这里i∈｛1，2，…，m｝，j∈｛m＋1，…，n｝．

证明　由于hij是常数，有dhij＝0，利用hijk＝0，以及

可以得到

利用矩阵（hil）是常数对角矩阵，可以写

利用（1．3．90）和（1．3．91），有

于是，当hii≠hjj时，必有

当ωji≠0时，必有hii＝hjj，利用第1讲内公式（1．1．19）和（1．1．20），兼顾p＝1，有

这里

当hii≠hjj时，利用连续性，在局部，hii不等于hjj．于是，在这一局部有（1．3．93）．那么，（1．3．94）的第一式左端等于零．于是，有

由于当ωjk≠0时，必有hjj＝hkk；同样当ωki≠0时，必有hkk＝hii，这与本段开始的假设hii≠hjj矛盾．因而ωjk，ωki二者中至少有一项是零．于是，有

由（1．3．95）和（1．3．96），可以得到，当hii≠hjj时，必有

这表明在M上，常数对角矩阵（hij）中至多有两个不相等的hii（1≤i≤n）．另外，要指出M上n个hii不可能全相等．用反证法．如果全相等，由于M是极小的，则所有hii全是零，矩阵（hij）是零矩阵，这与S处处等于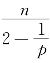（p＝1）＝n矛盾．因此引理5成立．

利用引理5，考虑方程组

利用第1讲内公式（1．1．17），有

利用引理5的（2），知ωρi＝0．那么，dωi＝0是ωi＝0（1≤i≤m）的代数推论．由Frobenius定理，在M内，方程组ωi＝0（1≤i≤m）是完全可积的．同理，方程组ωρ＝0（m＋1≤ρ≤n）也是完全可积的，这给出了M的一个局部分解．讲得仔细一点，即对于M的每个点，存在含这点的一个开邻域U，它是两个局部Riemann流形V1，V2的一个乘积V1×V2，这里didA1＝n－m，它由方程组（1．3．98）确定，dimV2＝m，它由方程组ωρ＝0（m＋1≤ρ≤n）确定．即e1，e2，…，em是V2的切空间的局部正交标架场，em＋1，…，en是V1的切空间的局部正交标架场．

利用引理5，V2的曲率

这里i，j，k，l∈｛1，2，…，m｝．V2是局部常曲率空间．

类似地，有V1的曲率

这里i，j，k，l∈｛m＋1，…，n｝．V1也是局部常曲率空间．

由于M是极小的等距浸入子流形，利用（1．3．21）（注意p＝1）及引理5，有

注意（hij）是常数对角矩阵，有

将公式（1．3．102）的两端乘以λ，再利用引理5（1）中λμ＝－1，有

于是，有两组解

由于当Sn＋1（1）内M的单位法向量en＋1改为－en＋1时，对应的矩阵（hij）改为（－hij），因此，只需考虑（1．3．105）的后一组解．

于是，利用引理5及公式（1．3．105）的后一组公式，可以看到Sn＋1（1）的联络形式（ωAB）（1≤A，B≤n＋1）限制于M，由下面（n＋1）×（n＋1）矩阵给出：

这里下标i，j∈（1，2，…，m｝，ρ，τ∈｛m＋1，…，n｝．

由于M⊂Sn＋1（1）⊂Rn＋2，利用（1．3．106）及Gauss公式（例如见［1］第251页），Rn＋2的联络形式（ωAB）（1≤A，B≤n＋2）限制于M，由下面（n＋2）×（n＋2）矩阵给出：

这与具有S＝n的Sn＋1（1）内闭等距浸入子流形M在Sn＋1（1）内的联络形式完全一样，仅仅在形式上多了一个上星号．那么，Mm，n－m在Rn＋2内的联络形式也完全等同于（1．3．107），仅仅在形式上多了一个上星号．由第2讲的定理1的证明过程可以看到，在给定一个初始条件的前提下，利用常微分方程组的Cauchy问题解的唯一性可以知道，完全可积Pfaff方程组的局部解是唯一的，因为Frobenius定理本质上是归结为常微分方程组的求解．因此，可以先作一个欧氏运动，使得初始点重合，初始点上的一组互相垂直的单位切向量叠合，利用对应的局部等距嵌入F只有一个，则M与Mm，n－m局部叠合．于是M与Mm，n－m的叠合部分既是开集，又是闭集，由于都是Sn（1）内闭（连通）超曲面，则M就是Clifford环面Mm，n－m．

②当p≥2时，S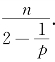＝．由公式（1．3．86）及本讲引理2可知，至多有2个矩阵Hα不是零矩阵．由于这时不等式（1．3．53）取等号，因此不可能只有一个Hα不是零矩阵．从而恰有2个矩阵不是零矩阵．

利用引理2，可以选择e1，e2，…，en，使得

当下标α≥n＋3时，Hα是零矩阵．

利用第1讲内公式（1．1．13）以及上式，有

在公式（1．3．126）中，令α＝3，i＝j＝1，兼顾（1．3．123）的第一个矩阵，知＝0，于是，有

如果有必要的话，可用－e3代替e3，用－e4代替e4．

综合上面叙述，有下述结论：

设M是Sn＋p（1）（p≥2）内等距浸入闭极小子流形，M的第二基本形式长度平方S恒等于常数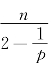，则n＝p＝2，且S4（1）内的联络形式（ωAB）限制于M由下列4×4矩阵给出：

这里λ，μ由（1．3．151）给定．

下面引入S4（1）内一个曲面M．

这里x2＋y2＋z2＝3．

明显地，可以看到

则是S4（1）内一张曲面，称为Veronese曲面．又由于X（－x，－y，－z）＝X（x，y，z），容易看到这个映射是实射影平面到S4（1）内的一个嵌入．

下面计算S4（1）内联络形式在这个Veronese曲面上的限制．

在R5内，e3，e4是垂直于e1，e2，Y的单位向量，因此，e3，e4是S4（1）内Veronese曲面的两个互相垂直的单位法向量．比较公式（1．3．165），（1．3．166）和（1．3．167），对应有

由Weingarten公式和上式，有

因此，S4（1）内联络形式（ωAB）限制于Veronese曲面上恰由表达式（1．3．152）给出．在R5内，Veronese曲面与S4（1）内S恒等于常数的闭曲面的联络形式完全一致．由第2讲的定理1，以及闭曲面和Veronese曲面的连通性，可以得到S4（1）内S恒等于常数的闭曲面恰是Veronese曲面．

于是，有

定理2　（S．S．Chern，M．Do．Carmo和S．Kobayashi）

（1）设M是Sn＋p（1）内一个n维闭极小等距浸入子流形，如果M的第二基本形式长度平方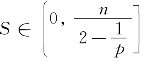，则S恒等于常数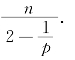

编者的话

这一讲内容来自第1讲编者的话中所提及的三人合作的文章．在20世纪80年代初，学习这篇文章是国内许多微分几何学者研究工作的起点．将球面Sn＋p（1）改成其他Riemann流形，或设法推进三人合作的定理，是当时不少人的工作．

参考文献

［1］白正国，沈一兵，水乃翔，郭孝英．黎曼几何初步（修订版）．高等教育出版社，2004．