欧氏空间内子流形的基本定理

2023-11-23 理论教育版权反馈

【摘要】：设M是欧氏空间Rn＋p内一个n维（局部）等距浸入子流形．记M在Rn＋p内的位置向量场为X，有M的第一基本形式这里〈，〉表示Rn＋p的内积，〈ei，ej〉＝δij．M沿单位法向量eα的第二基本形式这里利用了Weingarten公式．本讲的下标i，j，k，l，…，n．记利用的第一式，要证明考虑方程组是Rn×Rn＋p的一个开集内的n＋p个独立的Pfaff方程组，即在局部是含dx1，dx2，…，dFn＋p的一组独立的Pfaff方程组．而且满足及dF＝，i＝1，2，…

设M是欧氏空间Rn＋p内一个n维（局部）等距浸入（或等距嵌入）子流形．

记M在Rn＋p内的位置向量场为X，有

M的第一基本形式

这里〈，〉表示Rn＋p的内积，〈ei，ej〉＝δij．

M沿单位法向量eα（n＋1≤α≤n＋p）的第二基本形式

这里利用了Weingarten公式．本讲的下标i，j，k，l，…∈｛1，2，…，n｝；α，β，γ，…∈｛n＋1，…，n＋p｝；A，B，C∈｛1，2，…，n＋p｝．

由于M在Rn＋p内，利用第1讲公式（1．1．19），（1．1．20），（1．1．23），（1．1．24）和（1．1．34），有Gauss方程组、Ricci方程组和Codazzi方程组．反之，如果有一些函数在形式上满足上一讲的Gauss方程组、Ricci方程组和Codazzi方程组，会有什么情况呢？

下面的定理回答了这个问题．

注：本定理中条件蕴含着在M上存在C∞的1形式ωαβ，满足第1讲公式（1．1．24）．

先证明上述1形式ψAB满足下述方程组：

利用（1．2．4）的第二式，有

于是，可以看到

于是（1．2．5）成立．

现证明公式（1．2．6）．对于下标分段证明．当下标A＝i，B＝j时，利用（1．2．4）第一式，有

将（1．2．10）右端最后一项中的下标k换成j后，它与右端第四大项之和是零．将右端倒数第二大项中的下标k换成l后，与第二大项之和是零．将右端倒数第三大项中的下标k换成j，下标j换成l后，与右端第三大项之和是零．于是，在化简（1．2．10）后，有

当下标A＝α，B＝β时，有

从而公式（1．2．6）成立．

现在开始第二部分的证明．设存在一个等距嵌入F：U→Rn＋p，这里U是Rn内一个开集．F（U）在Rn＋p内的单位法向量场记为en＋1，…，en＋p．在映射F存在的前提下，有一个映射G，∀x∈U，(www.chuimin.cn)

因为上式右端每个向量都是Rn＋p内一向量，所以这里映射G是U到内一个映射．如果映射F是一个等距映射，则（1．2．13）右端是n＋p个互相正交的单位向量场．记

我们希望存在U上（n＋p）2个含n个自变量的光滑函数υAB（1≤A，B≤n＋p），满足

方程组（1．2．15）可视为内局部一开集上（n＋p）2个独立的Pfaff方程组．

在U内取任何以点O为起点的局部光滑曲线L（t），0≤t≤L*，这里L*是曲线长．

另一方面，利用（1．2．24），有

利用一阶常微分方程组Cauchy问题解的唯一性，有

于是，由（1．2．20）和（1．2．27）知道，是一组互相正交的局部单位向量场．

现在开始第三部分，即最后一部分的证明．需要证明存在一个映射F：U→Rn＋p，使得dF（ei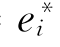）＝ pagenumber_ebook=26,pagenumber_book=18 ，i＝1，2，…，n．记

利用（1．2．17）的第一式，要证明

考虑方程组

（1．2．31）是Rn×Rn＋p的一个开集内的n＋p个独立的Pfaff方程组，即在局部是含dx1，dx2，…，dxn，dF1，dF2，…，dFn＋p的一组独立的Pfaff方程组．

而且满足（1．2．28）及dF（ei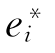）＝ pagenumber_ebook=28,pagenumber_book=20 ，i＝1，2，…，n．由于dF将一组n个互相垂直的单位正交向量场映成一组n个互相垂直的单位正交向量场，则F是一个局部等距映射．定理中的其余结论至此已一目了然．

编者的话

本讲是根据1979年出版的M．Spivak一书（第四卷）的第7章相关内容改写而成的（［1］）．另外，关于外微分形式的Frobenius定理，可参考我编的一本教材的第三章中的定理18（在§7，［2］）．

参考文献

［1］M．Spivak．A Comprehensive Introduction to Differential Geometry，Vol．4．Publish or Perish Inc．Berkeley，1979．

［2］黄宣国．李群基础（第二版）．复旦大学出版社，2007．

欧氏空间内子流形的基本定理

相关推荐