情景2 数学家维佛有一次和22 位将军一起用餐,他为了说明人们生日相同的概率有多大,开始在餐桌上询问各位将军的生日。情景3 《红楼梦》第六十二回写道:当下又值宝玉生日已到,原来宝琴也是这日,二人相同……不论是在《红楼梦》的描述中,还是在数学家的实验中,均可看到有两人生日相同,甚至有多人生日相同。......
2023-11-23
(1)模拟实验
将生日问题看作等概率的事件,则生日问题可看作有放回的随机抽取小球的试验,可以根据有放回抽球的试验特点,设置一个随机试验。
【试验前提】
①准备两组小球,一组为12 只完全相同的白球,二组为31 只完全相同的红球,分别代表12 个月份和每个月的31 日(或30 日、28 日),随机从一组与二组中各抽取一个小球,即记做一次模拟生日。
②若在实验过程中所抽取到的月份没有31 日,那么,抽取到31 日作废(若为2 月份,那么抽取到29 日、30 日、31 日均作废)。
【试验步骤】
①由随机抽取的试验者进行抽取,分别从一组和二组随机抽取一个小球,做记录。
②把所抽取的小球放回,进行下一次试验,依然进行同样的抽取。
③将此试验重复50 次,这样我们就可以得到50 位被测者的模拟生日,检查上面的50 个模拟生日,观察是否有相同的。
【结果分析】
分析50 个人中有两个人生日相同的概率(实际上该问题的理论概率约为97%)。 当试验次数很大时,一个事件发生的频率会稳定在相应的概率附近,因此,我们可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率。
事实上,还可用计算机产生的随机数进行模拟试验,从1 ~365 个数字中进行随机抽取,重复多次,也可得到试验结果。
(2)利用概率方法解析
【假设】
①以一年365 天计算(不考虑闰年)。
②不考虑双胞胎乃至多胞胎的现象。
③把每个人出生这一事件看作是等概率事件,不考虑其它影响因素。
④参加研究的人数不能超过365,否则事件将成为必然事件。
【分析】
假设每个人的生日在365 天中任意一天是等概率的,即皆为1/365,那么随机选取n 个人,其生日各不相同的概率为
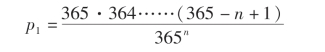 (www.chuimin.cn)
(www.chuimin.cn)
故n 个人中至少两个人的生日相同的概率为
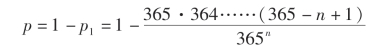
为简单起见,不妨将其变形为

根据泰勒级数展式,当x 较小时有e-x≈1 -x,用N 表示365,则有
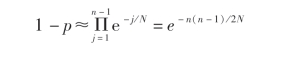
即
![]()
把N=365,n =5,10,15,20,…100 分别带入上式,可得表3.22.1 中的数值。
表3.22.1 n 个人中至少两人生日相同的概率

易见:在23 人中,至少有两人生日相同的概率已超过50%;在50 人中,至少有两人生日相同的概率可达97%。 故在一个60 人左右的班级里,我们几乎可以确定,至少有两个人的生日是相同的。
为使该问题更为直观,可根据表3.22.1 中的数据,利用Matlab 程序,画出生日问题的图像。
(程序):x=0:10:90;

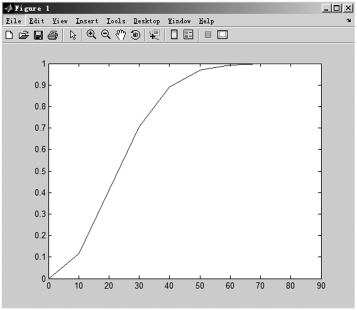
图3.22.1 人数与至少有两人生日相同概率分布图
《红楼梦》虽写了975 人,但着墨较多者也不过几十人,其中就给出好几对生日相同的人物,这与理论上的结果是相吻合的。 类似的问题还有“莎士比亚巧合”(莎士比亚生于1564 年4 月23 日,卒于1616 年4 月23,即生卒日相同),不少人为此大惊小怪,但从概率的角度看却是正常的。
随机性情形有时比确定性情形更有趣,偶然王国在某种意义上比必然王国更精彩。 在偶然王国里,切不可仅仅凭着直觉行事,因其有时并不可靠,而概率论作为一门严谨学科弥补了我们直觉上的某些缺陷。
有关数海拾贝:数学和数学家的故事的文章

情景2 数学家维佛有一次和22 位将军一起用餐,他为了说明人们生日相同的概率有多大,开始在餐桌上询问各位将军的生日。情景3 《红楼梦》第六十二回写道:当下又值宝玉生日已到,原来宝琴也是这日,二人相同……不论是在《红楼梦》的描述中,还是在数学家的实验中,均可看到有两人生日相同,甚至有多人生日相同。......
2023-11-23

于甜甜问,接着又轻快地笑了起来,“陶乐乐呀,我们在做什么……哦,我们正在给你做一件很有个性的生日礼物……嗯,DIY 知道吗?是DIY 生日礼物……你问要多长时间?我一个人要12个小时,杨彻一个人要18个小时,我先拼了6个小时,剩下的工作就归杨彻啦……啊?怎么?为什么不让我们做了?!哼——”于甜甜说着说着气鼓鼓地挂了电话。刘 叶 04-05 19:46:26生日礼物做完,陶乐乐的生日真的已经过去了吗?......
2023-07-30

存在拉应力的硬化层,容易产生裂纹,降低零件使用寿命,故在精加工后希望获得压应力硬化层。压应力的硬化层,一般在用滚压等加工方法时才能产生;而拉应力的硬化层,则在受较大摩擦力时就能产生,如用钝的切削刃切削时就会产生拉应力的硬化层。同时受拉应力硬化后的已加工表面一般都会被擦伤,对于冲击和变动载荷的抵抗较弱,因而影响了零件的使用性能。......
2023-06-24

为了顺利地进行下一步教学工作,不论学生对作品掌握是否娴熟,都要让学生在课堂上有完整演绎的机会。面对学生对于作品的完成和呈现,教师应该立即了解此作品中出现的基本问题,并给出相应的改正提升方法,处理完基本问题后,其他连带的细枝末节问题自然也会水到渠成。教师要严格要求学生做好课堂笔记,保证不遗漏重要内容,并在每次课前对前一次的笔记进行检查。......
2023-10-17

《公羊传·襄公二十一年》:“十有一月庚子,孔子生。”《十二诸侯年表》及《鲁周公世家》皆以孔子生于二十二年,后人遂取《穀梁传》之十月庚子,合以《史记》之说,以鲁襄公二十二年十月二十七日为孔子生日。又用阴历推之,定八月二十七日为孔子降诞之期。内称至圣先师生于鲁襄公二十二年庚戌之岁。则所谓二十一年十一月生者非矣。决非生圣人之年。必非生圣人之岁。虽皆持之有故,惟言日食岁不当生圣人,则近迂惑。......
2023-11-21

二八我在胡适家过生日和节日我二十岁生辰时是在芜湖第五中学读书,那日,我胡诌了一副对联。我的家眷还在家乡,单身在外,江冬秀要代我做生日,我不得已,就在她家请了两桌客。每逢佳节,江冬秀都要按照家乡的风俗来过节日。初八是腊八节,原来是佛家的节日。有一年,程士范住在胡适家,我约程和胡成之步行到前门外关帝庙看妓女烧香。又有一年,曹诚克住在胡适家过春节。......
2024-09-20

作为一名有“礼”的女人,就要懂得一些为朋友过生日的礼仪,以便能得体大方地送上自己的衷心祝福。另外,婴儿的周岁礼也很重要,同样应郑重庆贺。现代寿庆礼仪寿庆,俗称“做生日”,人逢周岁、16岁(弱冠)、20岁、寿诞均要庆祝。为同学或朋友庆祝生日,应该为他挑选一份生日礼物。生日礼物不必特别贵重,主要是表达自己的一份心意。......
2023-07-25

经过三年的发展,“北美留学生日报”已成为以留学新闻资讯为核心,集书籍出版、杂志、新媒体于一体的传媒机构。此外,有一件事情的发生,直接触发了创始人林国宇成立“北美留学生日报”的决心。几经筹备后,2014年1月1日,“北美留学生日报”正式上线。目前,“北美留学生日报”已通过广告等方式实现盈利,并在2016年4月获得了由小站教育领投的Pre-A轮1000万元融资。......
2023-10-31
相关推荐