奥雷姆：一次函数的研究及其应用

2023-11-23 理论教育版权反馈

【摘要】：后奥雷姆成为牧师,同时也是一位大学教授。而奥雷姆还有一个优越条件,就是得到国王的大力支持。图3.18.3奥雷姆对一次函数的研究奥雷姆对变量问题进行了研究。奥雷姆详细分析了匀加速直线运动,他用一条水平直线表示时间,直线上每一点代表一个时刻。速度随着时间均匀地增大,故线段长度也均匀增长,其端点构成一条直线。

西方关于坐标的概念可追溯到古希腊数学家阿波罗尼奥斯(Apollonius of Perga,约公元前262—前190),然而第一个给出一次函数关系者应是法国数学家奥雷姆(N. Oresme,1320—1382)。此前人们一直认为真理(规律)只有在静止状态下才能总结出来,故而未能用函数图像表示出变量之间的关系。

奥雷姆早年求学于巴黎大学,1348 年开始在纳瓦拉学院学习神学,并取得神学硕士学位。后奥雷姆成为牧师(后为主教),同时也是一位大学教授。西方中世纪的学者多半是神职人员,他们有着充裕的研究时间,生活来源还有保障,又有机会接触各种典籍文献。而奥雷姆还有一个优越条件,就是得到国王的大力支持。

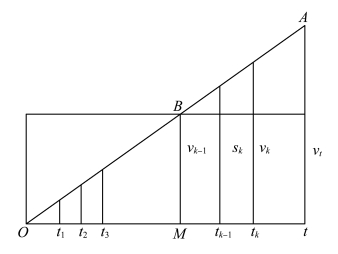
pagenumber_ebook=266,pagenumber_book=257

图3.18.3　奥雷姆对一次函数的研究(www.chuimin.cn)

奥雷姆对变量问题进行了研究。他认为,可测量皆为模拟量,如时间或长度,无论如何分割和截取其性质均不会改变。奥雷姆详细分析了匀加速直线运动,他用一条水平直线(相当于横坐标轴)表示时间,直线上每一点代表一个时刻。每个时刻对应着一个速度,该速度可用一条垂直于此点的线段来代表,其长度正比于速度的大小。速度随着时间均匀地增大,故线段长度也均匀增长,其端点构成一条直线(即一次函数)。该直线、水平直线和表示初速度、末速度的线段围成一个梯形。若初速度为0,则形成三角形OtA,其面积就是运动物体在时间t 内所通过的距离。

奥雷姆所应用的方法已接近现代解析几何,他使用图形表示随时间t 而变化的量vt,且把t 和vt 分别称为“经度”(相当于横坐标)和“纬度”(相当于纵坐标),这在当时是个了不起的创造。

奥雷姆：一次函数的研究及其应用

相关推荐