在一个能以统一观点把握宇宙的人看来，整个的造物过程就是一个具有唯一真理和必然发生的过程。犯了一系列小过失之后，隐形人认出了一位老相识，并把自己不同寻常的故事告诉了他。但这位朋友被吓坏了，并把格里芬先生的形迹报告了警察。由此发生了最后那场搜捕，在此过程中隐形人受了致命伤。像所有最好的科幻小说一样，威尔斯的许多故事中都有一定的科学根据。因为超空间的生灵会拥有超出人类之上、通常被说成是鬼神才具备的能力。......
2023-10-07
欧几里得平行理论的应用及意义
【摘要】：精确的定义,清楚的公设,严格的论证,这是欧几里得的目标。如图3.17.5 所示,欧几里得通过引辅助线CE,利用平行线性质,首先推出第一个结论,进而得到第二个结论。虽然欧几里得没有研究测量或度量公式,但他也证明了一些有关平行四边形和三角形面积比较的结论。虽然欧几里得的平行理论完全脱离了实物支撑,但展示了对数学美和数学理性的追求。
精确的定义,清楚的公设,严格的论证,这是欧几里得的目标。 由此他推证出一系列重要定理,如以命题29 为基础,推出三角形内角和定理。
命题32 在任意三角形中,若延长其一边,则外角等于二内对角之和,而且三角形的三个内角之和等于二直角。
如图3.17.5 所示,欧几里得通过引辅助线CE,利用平行线性质,首先推出第一个结论,进而得到第二个结论。 对于这样的基本定理,我们不仅可用剪刀将三个角进行拼接验证,更重要的是学会推理论证。 若仅仅是测量的话,那就几乎倒退到古埃及时代了。
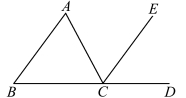
图3.17.5 命题32
(www.chuimin.cn)
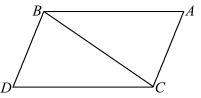
图3.17.6 命题33
命题33 在同一方向(分别)连接相等且平行的线段(端点),则连接线段亦相等且平行。
如图3.17.6 所示,欧几里得假设线段AB,CD 平行且相等,通过引进辅助线BC,推证出线段BD,AC 平行且相等,因而四边形ABCD 是一个平行四边形。 虽然欧几里得没有研究测量或度量公式,但他也证明了一些有关平行四边形和三角形面积比较的结论。
两条平行线走再久也不会有交点,两条平行线无法靠近也无法太远。 此乃欧几里得几何的基本性质,然而随着数学的进一步发展,非欧几何诞生了。 在非欧几何中,平行线是可以相交的;而且在同一平面内,过直线外一点,可以作无数条平行线平行于已知直线。
虽然欧几里得的平行理论完全脱离了实物支撑,但展示了对数学美和数学理性的追求。 分析其逻辑探索过程,使证明思路显露出来,可加深对公理化演绎体系结构的理解。 自古希腊时代以来,一代代人通过学习欧几里得几何掌握了逻辑推理方法。 随着几何学的发展,现代数学不仅成为推动其它学科进步的重要工具,而且本身也变成了一门魅力无穷的艺术。 深入美丽的数学王国,定会不断发现熠熠发光的珍珠。 让我们赶快扬帆起航,去寻找数学王国的珍珠吧!
有关数海拾贝：数学和数学家的故事的文章
- 详细阅读
-
深入探讨理论的本质及意义详细阅读
原因很简单——他们依据了不同的理论概念，从不同理论视角出发，同一个问题就会有不同的答案。士兵依据的是军事理论、艺术生依据的是绘画理论，农夫则从农业种植理论出发思考问题。可以说，这个故事生动演绎了理论何为。理论为人们理解世界、认识世界提供了不同的概念和认知方式，在此意义上，“理论”也是一种认知的媒介和工具，为人类各种社会实践活动和个体行为提供具有合理性、合法性的依据。......
2023-06-18
-
解决平行问题的作图方法及应用场景详细阅读
根据上述几何条件，解决平行问题作图的关键是直线的投影必须平行于平面内某条直线在同一投影面上的投影。在图形软件系统中，只要用好投影联系功能和画平行线功能，就能快速解决平行问题的作图问题。例3-29已知△ABC和点D的投影，过点D作一正平线DF平行于△ABC。作图先在△ABC中过点B取一条正平线BE。例3-31已知在△ABC和△FFG中，AB∥EF，试判断这两个三角形是否平行。......
2023-06-28
-
言语学习理论的重要性及意义详细阅读
奥苏贝尔的有意义言语学习理论就是用同化的思想来解释外在的逻辑意义怎样向个体的心理意义转化的过程和条件的学说。需要指出的是，概念学习与概念名称的学习是两种性质不同的有意义学习。有意义言语学习理论强调，在新知识的学习中，认知结构中原有的适当观念起决定作用。下面分别论述有关这三种关系的命题学习。......
2024-01-21
-
《冲淡》的理论实质及意义：中国古代美学新论！详细阅读
至宋代，在诗歌实践和理论方面都自觉、刻意、普遍地追求淡美。以此衡之，《冲淡》之冲淡实远于宋而近于陶。前文曾指出，陶诗是冲淡的典型代表。宋人的平淡，也常与理、意相关。[14]而对照来看，《冲淡》所展现的正是一片春色春意，洋溢的正是一派青春气息，而无丝毫暮色秋气。......
2024-03-24
-
物联网金融理论的发展及应用前景详细阅读
伴随着大数据、云计算、人工智能、物联网等技术方面的创新，金融科技将全面应用于支付结算、零售银行、财富管理等领域，金融与科技正在不断地进行深层次的融合。区块链、大数据、云计算、智能投顾等新技术伴随着物联网的发展而得以广泛应用，提高了资源配置效率，充分发挥了聚集信息的功能，促进银行、保险、证券、基金、信托等行业提供信息互联互通服务。金融科技公司与银行业之间的竞争使得价格信号能够较为灵敏地发挥作用。......
2023-08-13
-
企业市场创新理论与实践：实践意义及概念详细阅读
一产品整体概念及实践意义（一）产品的定义产品就是为顾客提供某种预期效益而设计的物质属性、服务和标记的组合。图4-1产品的整体概念在这里，我们以整体产品概念的五个层次为例说明整体产品概念。有形产品是产品的物质基础，其重要性不容否认。（三）产品整体概念的实践意义现代产品是一个具有三个或五个层次的整体概念，它是在营销实践中逐步发展起来的。产品整体概念的形成对保护消费者基本利益有着重要作用。......
2024-03-15
-
发明社会学中的英雄理论意义详细阅读
厄舍尔称其为一种“先验论”的观点。吉尔菲兰对发明的英雄观持否定态度，他明确指出“人们普遍误解了发明的本质”；“我们依然处于远古地质时代，对事物的产生认为是大洪水造成的灾变论的、而不是进化的观点，重大的发明被认为是某些伟人制造的”[11]。这一时期发明社会学理论表现出明显的否定英雄发明家的倾向。吉尔菲兰借用以下三个方面的理由来反对发明的英雄理论：个体发明者、发明的组合累积模式和发明的系统化、组织化。......
2023-11-27
相关推荐