对于由多个弯曲刚度EI为常数的杆段组成的结构,用图乘法计算位移的公式为显然,图乘法是将积分运算问题简化为求图形的面积、形心和竖标的问题。需要说明的是,用图乘法计算位移时,梁和刚架的杆件必须满足以下条件:杆段的弯曲刚度EI为常数。下面给出了图乘运算中几种常见图形的面积及其形心位置,如图13-14所示。......
2025-09-29
(1)《几何原本》中的乘法公式
资料表明,早在公元前1700 年左右,古巴比伦人已会用简单的乘法公式,当然他们是用文字表述。 例如问题:长乘宽得10,且长大于宽的量自乘之9 倍等于长自乘,试求长与宽。 若设长为x,宽为y,则有xy=10,9(x-y)2 =x2。
在欧几里得《几何原本》第二卷中,给出一系列乘法公式的文字叙述和逻辑证明,因未引进数学符号,叙述显得有些啰嗦。 如第二卷命题4 是这样叙述的:
命题4 若任意两分一条线段,则在整条线段上的正方形面积等于各个小段上的正方形面积之和加上由两小线段构成矩形面积的二倍。
如图3.16.1 所示,设点C 任意两分线段AB,AC = a,CB=b,则有
(a+b)2 =a2 +2ab+b2

图3.16.2 《几何原本》第二卷命题6
《几何原本》中也给出了著名的平方差公式,此即第二卷命题6。
命题6 若平分一条线段并且添加上另一条线段,则合成线段与添加线段构成的矩形面积与原线段一半上的正方形面积之和,等于原线段一半与添加线段之和上的正方形面积。
这个叙述让人有些费解,不过把关系理清楚就较为容易理解了。 如图3.16.2 所示,设点C 平分线段AB,并加上线段BD,则可证由线段AD、BD 构成的矩形面积与以CB 为边长构成的正方形面积之和,等于以CD 为边的正方形面积。 设AB=a,BD=b,则有

整理为
4(a+b)b+a2 =[(a+b) +b]2
2(a+b)b+a2 =(a+b)2 +b2
a2 -b2 =(a-b)(a+b)(https://www.chuimin.cn)
得
(2)贾宪三角还是帕斯卡三角
我国关于下式
展开系数规律的发现是在11 世纪中叶,比西方早600 年左右。 其发现者是北宋数学家贾宪。 贾宪曾在朝中任左班殿值,对《九章算术》颇有研究,著有《黄帝九章算经细草》和《释锁》,可惜两书均已失传。 幸运的是,两书部分内容均被杨辉(约13 世纪中)摘录进其《详解九章算法》(1261 年)之中。
杨辉是钱塘(今杭州)人,中国古代数学家和数学教育家。 曾任南宋地方行政官员,为政清廉,足迹遍及苏杭一带,著有数学书籍5 种21 卷。他非常重视数学教育,在《算法通变本末》中专为初学者制订的“习算纲目”是中国数学教育史上的重要文献。 根据杨辉的记载,贾宪约在公元1050 年完成了《黄帝九章算经细草》,首先使用“贾宪三角”进行高次开方运算,其基础是“开方作法本源”图。
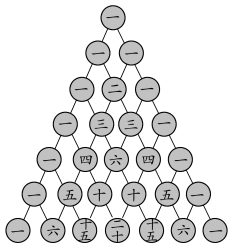
图3.16.3 贾宪三角
事实上,贾宪三角的第n 行就是二项展开式的系数列,三角形中的数字左右对称,对称轴是三角形底边上的“高”,除斜边上1 以外的各数,都等于它“肩上”的两数字之和,而所有这些数字排列的形状像等腰三角形。
元朝数学家朱世杰在其《四元玉鉴》(1303 年)中,扩充“贾宪三角”成“古法七乘方图”,使其变得更加实用。 《四元玉鉴》使我国古代数学达到巅峰。
法国数学家帕斯卡直到1654 年才发现这一数学规律。在其《算术三角形的规律》(Traité du Triangle Arithmétique)中,帕斯卡给出了一些相关结果,并以此创立了概率论。 因帕斯卡的学术影响在西方国家较大,故西方国家一直称之为“帕斯卡三角”。
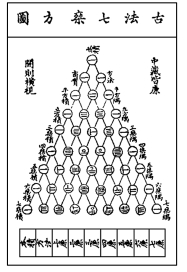
图3.16.4 古法七乘方图

图3.16.5 帕斯卡
近年来,国外一些学者也逐渐承认这项成果的优先权属于中国,有些文献已称之为“中国三角形”(Chinese Triangle)。 这是我们中国人的骄傲。
相关文章

对于由多个弯曲刚度EI为常数的杆段组成的结构,用图乘法计算位移的公式为显然,图乘法是将积分运算问题简化为求图形的面积、形心和竖标的问题。需要说明的是,用图乘法计算位移时,梁和刚架的杆件必须满足以下条件:杆段的弯曲刚度EI为常数。下面给出了图乘运算中几种常见图形的面积及其形心位置,如图13-14所示。......
2025-09-29

=f=e0=1,f(n+1)(θx)=eθx.故f=ex的n阶麦克劳林公式为例2 求f=sinx的带有拉格朗日型余项的n阶麦克劳林公式.解 ,所以f=0,f′=1,f″=0,f=-1,f=0,…从而其中,例3 求.解 ,,所以原式.几个常用函数的麦克劳林公式:由以上带有佩亚诺型余项的麦克劳林公式,易得相应的带有拉格朗日型余项的麦克劳林公式,读者可自行写出.......
2025-09-30

方法设定200为基准数,计算出两个数与200之间的差。将上两排数字交叉相加所得的结果写在第三排的左边。例子计算186×192=______先计算出186、192与200的差,分别为-14,-8,因此可以写成下列形式:186/-14192/-8交叉相加,186-8或192-14,都等于178。因此可以写成:203/3212/12215/36215×200+36=43036所以203×212=43036扩展阅读类似的,你还可以用这种方法计算接近250、300、350、400、450、500、550……等数字的乘法,只需选择相应的基准数即可。......
2025-09-30

一、积分变上限函数设函数f(x)在区间[a,b]上连续,并且设x为[a,b]上的一点.则函数f(x)在部分区间[a,x]上的定积分∫xaf(x)dx存在且连续,为了区分积分变量,我们用t表示积分变量,记为定理1(微积分基本定理)如果函数f(x)在区间[a,b]上连续,则积分变上限函数在[a,b]上具有导数,并且它的导数为图5.8定理1表明,Φ(x)是连续函数f(x)的一个原函数,因此可得.定理2......
2025-09-30

(一)教学内容生活中的乘法问题。①点评学生找到的生活中的乘法问题,指出优点和需要改进的地方。每人精心准备三个除法问题。准备时注意尽量选取不同类型、不同情景下的除法问题。在上一节活动课,教师对如何发现生活中的乘法问题做了充分的说明和示范。另外,全班汇报时,可以抽取一部分小组汇报生活中的乘法问题,一部分小组汇报体会收获,提高课堂效率,避免汇报用时过长而带来的疲倦感。......
2025-09-29

① 打开Excel工作簿,单击“插入”→“文本”选项组中的“对象”按钮,打开“对象”对话框。② 选择“新建”选项卡下的“Microsoft公式3.0”选项。图3-14⑤ 保持插入的公式模板状态不变,继续单击“围栏模板”按钮,在下拉菜单中单击按钮。⑦ 单击后继续在模板中输入需要的数值,然后将后面的公式补充完整,按
2025-09-30

【主要内容】1.带拉格朗日型余项的泰勒公式设函数f(x)在[a,b]上具有直到n阶的连续导数,在(a,b)内具有n+1阶导数,则对x0∈[a,b],有(x∈[a,b]).(1)其中,余项,ξ是介于x0与x之间的实数).设函数f(x)在(a,b)上具有直到n+1阶导数,则对x0∈(a,b),有其中,余项,ξ是介于x0与x之间的实数).式(1)和式(2)称为f(x)按(x-x0)的幂展开的带拉格朗日型......
2025-09-30

【知识点回顾】一般而言,如果x与y的函数关系隐含在方程F(x,y)=0中,即x在某一区间取值时,相应地有确定的y值和其唯一对应,则称方程F(x,y)=0所确定的函数为隐函数.隐函数求导步骤:(1)方程两边对x进行求导;(2)在求导过程中把y看成x的函数y=f(x),用复合函数求导法则进行.一、二元函数的情形在第二章第六节中已经提出了隐函数的概念,并且指出了不经过显化直接由方程求它所确定的隐函数的方......
2025-09-30
相关推荐