数学家与一元一次方程

2023-11-23 理论教育版权反馈

【摘要】：《九章算术》中有不少一元一次方程问题,这些问题大多出现在少广章、均输章和盈不足章等,而方程章则主要是线性方程组及其解法。以一为二,半为一,并之得三,为法。瓜生其上,蔓日长七寸。综上,类似的一元一次代数方程问题,在东西方文明的发展中都遇到了。

《九章算术》中有不少一元一次方程问题,这些问题大多出现在少广章、均输章和盈不足章等,而方程章则主要是线性方程组及其解法。

少广章第1 题今有田广一步半,求田一亩,问从(纵)几何?

答曰:一百六十步。

术曰:下有半,是二分之一。以一为二,半为一,并之得三,为法。置田二百四十步,亦以一为二乘之,为实。实如法得从步。

题目大意为:今有长方形田地一块,其宽为3/2 步,若田地的面积为1 亩(240 平方步),求其长度。

这个问题甚是简单,相当于求解方程

容易解出其解为160 步。

按照术曰,虽未设定未知数,但其计算过程与解方程类似:

因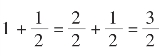 pagenumber_ebook=244,pagenumber_book=235 ,有240 ×2 ÷3 =160(步)。

均输章12 题今有善行者行一百步,不善行者行六十步。今不善行者先行一百步,善行者追之,问几何步及之。

此即追及问题。不妨设善行者速度为1,则不善行者速度为3/5。若善行者x 步赶上不善行者,则有

易得善行者250 步就能赶上不善行者。

均输章20 题今有凫(野鸭)起南海,七日至北海;雁(大雁)起北海,九日至南海。今凫雁俱起,问何日相逢。

刘徽在注释《九章算术》时,给出如下求解方法:

设野鸭和大雁x 天相遇,南北海之间的距离为1 个单位,则分别得野鸭和大雁的飞行速度为1/7 和1/9,由题意得(www.chuimin.cn)

易解得野鸭和大雁天相遇。

均输章26 题今有池,五渠注之。其一渠开之,少半日一满;次,一日一满;次,二日半一满;次,三日一满;次,五日一满。今皆决之,问几何日满池。

题意为:今有一水池,用5 条渠道输水。若仅打开第一条渠,1/3 日把池灌满;若仅打开第二条渠,1 日把池灌满;若仅打开第三条渠,5/2 日把池灌满;若仅打开第四条渠,3 日把池灌满;若仅打开第五条渠,5 日把池灌满。若5 条渠道同时打开,问几日可把池子灌满。

这相当于解方程

易解得日可把池子注满。

均输章27 题今有人持米出三关,外关三而取一,中关五而取一,内关七而取一,余米五斗(一斗为10 升)。问本持米几何。

这相当于解方程易解得原来带米升。

盈不足章10 题今有垣高九尺。瓜生其上,蔓日长七寸。瓠(葫芦)生其下,蔓日长一尺。问几何日相逢。

这相当于解方程

10x+7x=90

易解得日相遇。

此题若是应用“盈不足术”解答,则没有如此简洁。不过“盈不足术”可谓“万能”解法,充分反映了我国古人数学思想之博大精深。

综上,类似的一元一次代数方程问题,在东西方文明的发展中都遇到了。千百年来数学对人类文明产生了毋庸置疑的深刻影响,对人们的思维方式、教育方式、生活方式以及世界观、艺术观有着潜移默化的影响,以其思维的严密性和理性的探索精神为人类认识世界和改造世界提供了强有力的支持,为人类文化的发展提供了方法论基础和科学技术手段。

数学家与一元一次方程

相关推荐