数海拾贝：欧几里得与全等三角形判定

2023-11-23 理论教育版权反馈

【摘要】：在欧几里得之前,几何学多是片断、零碎的知识,公理与公理间、证明与证明间并无较强的联系,更不要说对定理的严格论证。在其证明过程中,欧几里得应用了公理4:彼此重合的图形是全等的。不少人不满意欧几里得的该证明,而另辟蹊径。图3.13.4角边角定理证明对于命题26 的证明,欧几里得没有利用三角形内角和定理,而是分别对“等角夹边”和“等角对边”两种情况进行了证明,其中应用了反证法。

在欧几里得之前,几何学多是片断、零碎的知识,公理与公理间、证明与证明间并无较强的联系,更不要说对定理的严格论证。欧几里得敏锐察觉到几何学的发展趋势,试图把几何学知识加以条理系统化。他一边搜集数学专著和手稿,一边著书立说阐明对几何学的理解,通过多年努力,最终完成了几何学不朽之作——《几何原本》。 “原本”的希腊文是指一学科中具有广泛应用的最重要定理。而关于三角形全等的3 个判定定理分别是第一卷的命题4(边角边定理)、命题8(边边边定理)和命题26(角边角定理)。

pagenumber_ebook=233,pagenumber_book=224

图3.13.1　阿拉伯文《几何原本》一页

(1)边角边定理

命题4 若在两个三角形中,有两条边分别对应相等,且相等线段的夹角亦相等,则其底边相等、两个三角形全等,进而其余对应角亦相等(等边所对角)。

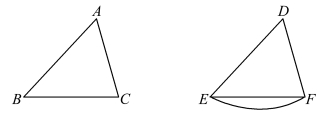
pagenumber_ebook=234,pagenumber_book=225

图3.13.2　边角边定理证明

这里的叙述几乎是沿用了《几何原本》原文,故显得有些啰嗦。对于该命题的证明,欧几里得应用了叠置法,即把一个三角形“移动”到另一个三角形上。此前他给出了线段的重叠定义,但未给出“角重叠”的定义,因而其证明显得有些勉强,无异于假设存在不改变几何图形形状与大小的运动。

设在△ABC 和△DEF 中,AB = DE,AC = DF,∠BAC =∠EDF,则可证BC = EF,△ABC≌△DEF,∠ABC = ∠DEF,∠ACB=∠DFE。

若移动△ABC 到△DEF 上,使点A 落在点D 上,且线段AB 落在DE 上,因AB=DE,则点B 与点E 重合,有AB 与DE重合。

因∠BAC = ∠EDF,线段AC 落在线段DF 上,而AC =DF,故点C 与点F 重合。

可以推断,底BC 与底EF 重合(若点B 与点E 重合,且点C 与点F 重合,而底BC 与底EF 不重合,则两点可以决定两条直线,根据公设1,这是不可能发生的)。

可得,△ABC 与△DEF 完全重合,因而两者全等。故而其余角也重合,于是它们皆相等。

在其证明过程中,欧几里得应用了公理4:彼此重合的图形是全等的。

(2)边边边定理

命题8 若在两个三角形中,有两条边分别对应相等,且其底边亦相等,则夹在等边中间的角亦相等。

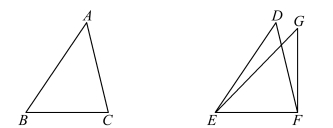
pagenumber_ebook=235,pagenumber_book=226

图3.13.3　边边边定理证明

为了证明命题8,欧几里得首先证得:

命题7 在已知线段上,从其两个端点作出相交于一点的两条线段,则不可能在该线段的同侧作出相交于另一点的另外两条线段,使得所作两线段分别等于前面两条线段,即两个交点到相同端点的线段相等。

欧几里得还是采用了重叠法,但其中应用了反证法。

设在△ABC 和△DEF 中,有AB=DE,AC=DF,BC=EF,则可证∠BAC=∠EDF。

若移动△ABC 到△DEF 上,使点B 落在点E 上,线段BC落在EF 上,则点C 与和点F 重合。

而BC = EF,故BC 和EF 重合,BA、AC 分别与ED、DF重合。

事实上,若底BC 和底EF 重合,而边BA、AC 不与ED、DF重合,落在其旁的EG、GF 之上,则在已知线段(其一端点为上方线段一端点)上方有相交于一点的两条线段,同时在同一线段(其一端点为上方线段一端点)的同侧又作出了交于另一点的另外两条线段,而它们分别等于前面两条线段,即两个交点到同一端点的连线相等,根据命题7,不可能作出后两条线段。(www.chuimin.cn)

因此,△ABC≌△DEF。

因而有∠BAC 和∠EDF 重合,即它们相等。

不少人不满意欧几里得的该证明,而另辟蹊径。如费罗(Philo,约公元前1 世纪)所给证明为:移动一个三角形,使其一条边与另一个三角形的对应边重合,而该边所对顶点与另一个三角形的对应顶点位于其两侧,连结这两个顶点,则得到两个等腰三角形,故知重合边所对角相等,根据边角边定理,问题得证。

(3)角边角定理

命题26 若在两个三角形中,有两个角分别对应相等,且有一条边亦相等(等角夹边或等角对边),则它们的其他边亦相等。

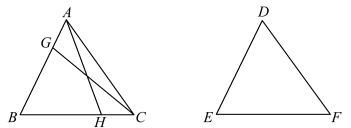
pagenumber_ebook=236,pagenumber_book=227

图3.13.4　角边角定理证明

对于命题26 的证明,欧几里得没有利用三角形内角和定理,而是分别对“等角夹边”和“等角对边”两种情况进行了证明,其中应用了反证法。相对于前两个命题,本命题证明显得有些冗长(下面的证明做了一些精简),故而有些数学家不满意欧几里得的证明,如阿拉伯数学家阿尔·奈里兹(AL-Nairizi,约10 世纪)在注释《几何原本》时,仍采用了叠置法。对于同一个问题,数学家虽有不同见解,但在其学术个性背后,仍有着共性,即甘于寂寞、坚韧不拔的潜心钻研精神。数学家的灵光一现不是空穴来风,而是根植于其对所研究对象本质的深入理解。

欧几里得的证明如下:

设在 △ABC 和 △DEF 中, 有 ∠ABC = ∠DEF,∠ACB=∠DFE。

①假定相等边为等角所夹边,即BC =EF,则需证AB =DE,AC=DF,∠BAC=∠EDF。

采用反证法。若AB≠DE,则两者之中必有较长者,不妨设其为线段AB。取BG=DE,连接GC,因BG=DE,BC=EF,∠GBC=∠DEF,由前述命题4 可知,△GBC≌△DEF。故有∠GCB=∠DFE,但∠ACB =∠DFE,则∠ACB =∠GCB,导致矛盾。

因此,AB=DE。

而BC = EF,∠ABC = ∠DEF,由命题4 可知,△ABC≌△DEF

所以,AC=DF,∠BAC=∠EDF。

②假定为等角所对边相等,不妨设AB = DE,则需证BC=EF,AC=DF,∠BAC=∠EDF。

采用反证法。若BC≠EF,则两者之中必有较长者,不妨设其为线段BC。

令BH=EF,连接AH,由命题4 可知,△ABH≌△DEF。

则有∠AHB = ∠DFE。但∠DFE = ∠ACB,于是,在△AHC 中,有外角∠AHB 等于内对角∠ACB,显然矛盾。

所以BC=EF,因AB =DE,且∠ABC =∠DEF,有△ABC≌△DEF。