教学中要引导学生抓住长方形、正方形四边之和，通过多种算法的比较，指出其本质都是求出长方形、正方形的周长；再利用长方形、正方形的图形特点，推导、归纳长方形和正方形周长的计算公式。这有利于学生从中得到启发，逐步掌握并不断优化长方形周长的计算方法。引导学生根据正方形的特点以及周长的含义，得出正方形的周长是把四边相加。......
2023-07-27
几何原本：矩形和正方形的关系
【摘要】：《几何原本》第二卷主要讨论了不同的矩形和正方形的关系,其中多数命题可用现代代数符号解释,即是用几何图形表示代数概念和运算。命题4 若任意两分一条线段,则在整条线段上的正方形面积等于各个小段上的正方形面积之和加上由两小线段所构成矩形面积的二倍。“方”是指正方形或长方形,且含有单位面积之意。但是四边形四条边的长度确定后,却可以组成不同的四边形:正方形、菱形、矩形等。
《几何原本》第二卷主要讨论了不同的矩形和正方形的关系,其中多数命题可用现代代数符号解释,即是用几何图形表示代数概念和运算。 第二卷从矩形定义开始:任何矩形都是由形成直角的两条线段构成。
这一定义并未说明矩形面积等于其长和宽的乘积,因欧几里得当时还无法给出任意长度的乘法定义,故他从未把长和宽相乘。
命题1 如果有两条线段,其中一条被截成任意几段,则原来两条线段构成的矩形面积等于各个小段和未截那条线段构成的矩形面积之和。
图3.12.10 《几何原本》卷二命题1
假设已知L、BC 是两条线段,用点D、E 分线段BC,则L、BC 所构成矩形的面积等于几个小矩形的面积之和。 若L 的长度为l,三个小矩形另一边的长度分别记为a,b,c,此即乘法分配律:l(a+b+c) =la+lb+lc。
命题4 若任意两分一条线段,则在整条线段上的正方形面积等于各个小段上的正方形面积之和加上由两小线段所构成矩形面积的二倍。(www.chuimin.cn)
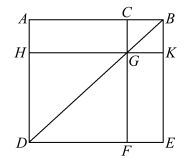
图3.12.11 《几何原本》卷二命题4
假设点C 任意两分线段AB,则可证以AB 为边的正方形面积等于以AC 和BC 为边的正方形面积加上以AC 和BC 为边的长方形面积的二倍。 这一命题可表示为:(a +b)2 =a2 +b2 +2ab。
我国经典数学著作《九章算术》的第一章方田,主要是各种不同形状田地面积的计算。 “方”是指正方形或长方形,且含有单位面积之意。 我国古时也称长方形的田为直田或广田。 其中给出各种形状的土地面积计算法,主要有方田(长方形)、圭田(等腰三角形)、邪田(直角梯形)、箕田(等腰梯形)、圆田(圆形)、宛田(球冠形)、弧田(弓形)、环田(圆环或环缺形)等,除宛田、弧田用近似计算法外,其它图形面积算法都是正确的。 方田章前两题就揭示出长方形的面积等于长乘以宽。 这就表明,公元1 世纪前,我国数学家通过对一些实际问题的研究,得出了一般长方形面积的算法公式,进而再广泛应用于现实问题之中。
给定三条边长,三角形就可以唯一确定。 但是四边形四条边的长度确定后,却可以组成不同的四边形:正方形、菱形、矩形等。 而且四边形可以有凹角,四条边也可不在一个平面内。 故从三角形到四边形虽然仅仅增加了一条边,但其本质上却有了很大差异。
有关数海拾贝：数学和数学家的故事的文章
- 详细阅读
-
小学三年级数学教学策略：认识长方形和正方形，详细阅读
重/难点分析重点分析：认识长方形和正方形的特点，不仅是学习周长的基础，也是以后学习长方形、正方形面积，以及其他一些平面图形和立体图形的基础，同时还有利于学生逐步建立空间观念。......
2023-07-27
-
中心极限定理：揭示随机变量和正态分布的关系详细阅读
如前所述，大数定律揭示了大量随机变量的平均结果的稳定性，但没有涉及随机变量的分布。而中心极限定理则进一步揭示出大量相互独立的随机变量之和近似服从正态分布的一般规律，可以用于计算任一随机结果发生的具体概率。中心极限定理以严格的数学形式阐明了在大样本条件下，不论总体的分布如何，样本的均值总是近似地服从正态分布。这使得正态分布在数理统计中具有很重要的地位，并得到了广泛应用。......
2023-08-11
-
退火和正火的概念简介详细阅读
图2-1各类退火及正火工艺加热温度示意按退火目的也可以将其分成两大类，一类是将工件加热到一定温度，保温停留较长时间，使不平衡状态依靠浓度梯度、应力梯度和界面能等，自发由不平衡状态过渡到平衡状态。这类退火包含扩散退火、预防白点退火、再结晶退火、去应力退火等。这类退火包含完全退火、不完全退火和球化退火等。有色金属工件的退火工艺主要有铸态下的扩散退火、变形合金的再结晶退火和去应力退火等。......
2023-06-24
-
同素材命题间关系揭示于逻辑正方形《韦卓民全集详细阅读
逻辑正方形和其说明如下：逻辑正方形的形成：逻辑正方形是以A、E、I、O 这四种同素材的命题类型而形成的。逻辑正方形所表示的四种命题对当关系。上位与下位命题的关系是全体与部分的关系，但不一定是类与种的关系，因为“所有的人”不是“有些人”的类。通常在形式逻辑上，“有些”是作第一种的解释。它们的关系，最容易是通过矛盾关系而看出。......
2023-11-08
-
钢的退火和正火选择原则详细阅读
③消除过共析钢的网状碳化物，便于球化退火。过共析钢在淬火之前要进行球化退火，以便于机械加工并为淬火作好组织准备。退火与正火的选择原则如下所述。......
2023-06-23
-
三视图和正确位置详细阅读
1．在正面内得到的由前向后观察物体的视图叫做________，在水平面内得到的由上向下观察物体的视图叫做_________，在侧面内得到的由左向右观察物体的视图叫做_________．2．三个视图要放在正确的位置，并且主视图和俯视图的________，主视图和左视图的________，左视图和俯视图的_________．1．下列立体图形中，俯视图是三角形的是（ ）．（第2题）2．鼓作为一种打击乐器......
2023-07-03
-
Illustrator应用设计：矩形的创建和详细阅读
首先创建一系列矩形，它们是明信片图稿的开始。拖动直到矩形显示为宽约l.25英寸且高为1.5英寸时为止，如图4.3所示。图4.3矩形精确绘制拖动以创建形状时，鼠标指针旁边出现的工具提示被称为度量标签，它是智能参考线的一部分，本课稍后会介绍智能参考线。接下来，将通过输入值而不是绘制来创建另一个矩形。单击“确定”以创建一个与之前绘制的形状大小完全相同的新矩形。保持选中矩形，为下一步做准备。它应该仍位于上方矩形的下方。......
2023-11-20
相关推荐