新生事物的出现往往会引来一些嘲讽,琼斯的圆周率符号也不例外。由于数学大师们的影响,圆周率符号π 得到了广泛认可和应用。反观国内,在我国古代圆周率没有明确的符号表示。直至20 世纪初期,我国数学教科书由直排改为横排之时,才与世界数学接轨,用符号π 表示圆周率。如在1932 年的《初级混合算学》中,就载有“圆周与直径之比,通常表示以π”。......
2023-11-23
数学和数学家的故事：三角形和平行四边形
【摘要】：命题41 若一个平行四边形和一个三角形既同底又在两平行线之间,则平行四边形面积是三角形的2 倍。图3.12.7《几何原本》卷一命题43若AC 为ABCD 的对角线,则其所谓平行四边形补形为BGKE 和KFDH。利用三角形全等可以证明之。图3.12.8《几何原本》卷一命题44若已知线段为AB,直线角为D,三角形为C,求作以AB为一边、某底角等于∠D、面积等于三角形C 的平行四边形。连接BD,则问题就转化为作两个平行四边形,其面积分别等于两个三角形的面积。
大家知道,两个全等三角形可以拼成一个平行四边形,同底等高的平行四边形面积是三角形的2 倍(《几何原本》卷一命题41)。 如何作一个平行四边形,使其面积等于已知三角形? 欧几里得给出一种作法(《几何原本》卷一命题42)。
命题41 若一个平行四边形和一个三角形既同底又在两平行线之间,则平行四边形面积是三角形的2 倍。
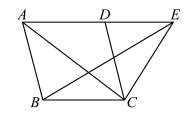
图3.12.5 《几何原本》卷一命题41
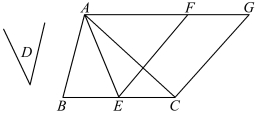
图3.12.6 《几何原本》卷一命题42
▱ABCD 和△BCE 满足定理条件,连接线段AC,则易知△ABC 和△BCE 面积相等,再利用命题34,命题得证。
命题42 以已知直线角求作平行四边形,使其面积等于已知三角形。
命题42 进一步沟通了平行四边形和三角形之间的联系,所作平行四边形的一个底角等于已知直线角,其面积等于已知三角形面积。
命题41 和命题42 可谓相辅相成。 前者是把平行四边形分解为三角形;后者把三角形转化为面积相等的平行四边形,且在某底角确定时是唯一的。
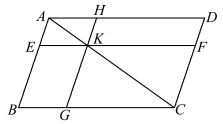
命题43 在任意平行四边形中,对角线两边的平行四边形补形面积相等。
(www.chuimin.cn)
图3.12.7 《几何原本》卷一命题43
若AC 为▱ABCD 的对角线,则其所谓平行四边形补形为▱BGKE 和▱KFDH。 利用三角形全等可以证明之。
命题44 用已知的线段、直线角和三角形,求作平行四边形,使其面积等于已知三角形。
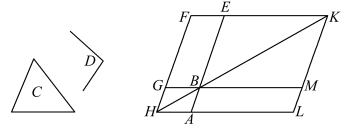
图3.12.8 《几何原本》卷一命题44
若已知线段为AB,直线角为D,三角形为C,求作以AB为一边、某底角等于∠D、面积等于三角形C 的平行四边形。欧几里得利用平行线的性质,作出▱ABML,其面积等于三角形C 的面积,∠ABM 等于直线角∠D。
命题45 用已知直线角,求作平行四边形,使其面积等于已知直线形。
已知直线角∠E 和直线形ABCD,求作平行四边形,使其面积等于直线形ABCD 的面积。 连接BD,则问题就转化为作两个平行四边形,其面积分别等于两个三角形的面积。 故命题45 是命题44 的推广。
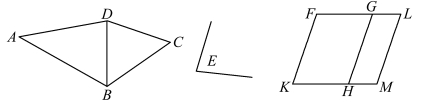
图3.12.9 《几何原本》卷一命题45
有关数海拾贝：数学和数学家的故事的文章
- 详细阅读
-
西方分式方程理论：数学和数学家的故事详细阅读
英国著名盲人数学家、剑桥大学第四任卢卡斯数学教授桑德森可能是西方第一个研究分式方程的数学家。作为其解题过程的一部分,桑德森接着给出上述解法的逆过程。可见他已意识到解分式方程的过程应该是可逆的,但其是否知道在分式方程变换过程中可能出现增根和失根问题尚待进一步考证。若设乙所需天数为x,则甲为x+4,因而可列分式方程易得x=10。......
2023-11-23
-
研读《数海拾贝：数学和数学家的故事》，探寻数详细阅读
表1.6.1马克思求解不定方程数值表因x=10 时,y=0,与题意不符,故前9 组均为方程的解。约从19 世纪60 年代起,马克思开始学习微积分,研读了牛顿的《自然哲学的数学原理》、欧拉的《无限分析引论》《微分学基础》、穆瓦尼奥的《微分学讲义》、拉克罗阿的《微积分学》、布沙拉的《微积分学与变分学》、赫明的《初等微积分学》、拉格朗日的《解析函数论》、达朗贝尔的《流体论》等在数学史上影响较大的著述。......
2023-11-23
-
达·芬奇的数学情结：数学家的故事详细阅读
达·芬奇深刻认识到数学方法的重要性,并掌握了一些数学原理。在《最后的晚餐》中,达·芬奇应用了大量数学知识。达·芬奇的其他代表作《蒙娜丽莎》《岩间圣母》等也为世人所赞扬。......
2023-11-23
-
埃里冈对几何学符号的创用和改进：数学家的故事详细阅读
虽然人类对角的认识由来已久,但直至埃里冈才第一次给出角的表示符号“ <”。埃里冈选用符号“ =”表示平行大概亦是基于如此理念,但当时欧洲已使用符号“ =”作为等号,为避免混乱,英国数学家奥特雷德改用符号“∥”来表示平行,显然是将等号逆时针旋转45 度并拉长而得到。埃里冈采用符号“◇”表示平行四边形,现在看来有些勉强。......
2023-11-23
-
函数概念引入中国：数学家和数学的故事详细阅读
直至1859 年,数学术语“function”才被引进中国,如何准确翻译成汉语没有先例。现今函数概念及其表示符号可谓充斥着数学王国,也成为我们生活中的重要组成部分。回顾17 世纪上半叶到现在300 余年函数概念的演进历程,充分表明了严密化的企图始终刺激着数学科学的发展。从笛卡儿、莱布尼茨、欧拉,再到李善兰,他们对函数的发展均做出了重要贡献,故函数概念及其表示符号实在是经过了千锤百炼,是一代代数学家集体智慧的结晶。......
2023-11-23
-
因式分解的起源和方法-数学家的故事详细阅读
因式分解的最初目的是为了快捷求解代数方程,对此许多数学家做了尝试,最终凝练成我们今天熟知的一些规律。韦达和哈里奥特韦达在其《论方程的整理和修改》中,首先给出代数方程的多项式因式分解方法,并证得所有三次和三次以上的一元多项式在实数范围内皆可因式分解。笛卡儿与因式分解1637 年笛卡儿在其《几何学》中,首次应用待定系数法将4 次方程分解为两个2 次方程求解,并最早给出因式分解定理。......
2023-11-23
-
中国概率论的发展：数学与数学家的故事详细阅读
据现有资料分析,中国概率论可划分为5 个发展阶段。许宝騄是20 世纪最富有创造性的统计学家之一,是中国最早从事概率论与数理统计研究并达到世界先进水平的优秀数学家。其研究成果已经成为概率论与数理统计理论的重要组成部分,至今“许方法”仍被认为是解决检验问题的最实用方法。此为中国概率论学科发展的重要里程碑。......
2023-11-23
相关推荐