首页理论教育3个步骤计算三角形面积

3个步骤计算三角形面积

2025-09-30 理论教育版权反馈

【摘要】：史载古巴比伦人已能计算三角形的面积,不过在其所用公式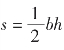中,未明确指出长度为b 与h 的两条直线是否互相垂直。这些田地一般为四边形,若四条边分别记为a,b,c,d,其中a 与b、c与d 是相对边,则田地面积公式为而对于三角形来说,则认为d 就没有了,因而有在《九章算术》中,已有正确的三角形面积公式。关于三角形的面积计算有两道题:25.今有圭田广十二步,正从二十一步。可见在第26 题的“术”中,给出了三角形的面积计算方法。

史载古巴比伦人已能计算三角形的面积,不过在其所用公式 pagenumber_ebook=221,pagenumber_book=212 中,未明确指出长度为b 与h 的两条直线是否互相垂直。另外古巴比伦人还给出一种反映不同几何图形的某些数学关系的常数表,如对三角形给出系数1/2,意指三角形面积是高与长乘积的一半;对三角形的高给出系数7/8,指等边三角形的高为底的7/8 等,当然有些结果只是近似值。

埃及虽是几何的发源地,但其始终停留在实用阶段,未能发展成为系统的几何学。关于三角形的面积计算,埃及人给出一个不正确的公式:

在莱茵德纸草书中有一道求三角形面积的题目:三角形的底为4,边为10,求其面积。原书所给结果为20,因而需要弄清楚“边”是什么,若是直角边,那结果就是正确的,否则就是应用了错误公式。

在古埃及艾德福庙宇墙上刻有捐献的田地表。这些田地一般为四边形,若四条边分别记为a,b,c,d,其中a 与b、c与d 是相对边,则田地面积公式为

而对于三角形来说,则认为d 就没有了,因而有

在《九章算术》中,已有正确的三角形面积公式。《九章算术》因分九章而得名,全书有246 道题,每题有问、答、术(解决方法),涉及的问题皆源于现实生活。关于三角形的面积计算有两道题:

25.今有圭田广十二步,正从二十一步。问为田几何?

答曰:一百二十六步。

26.又有圭田广五步二分步之一,从八步三分步之二。(https://www.chuimin.cn)

问为田几何?

答曰:二十三步六分步之五。

术曰:半广以乘正从。

可见在第26 题的“术”中,给出了三角形的面积计算方法。其中“广”为等腰三角形的底,“从”(音zòng)为高,故所给出的三角形面积计算公式为

于是,有

25.解:

26.解:

刘徽对计算公式作了说明:半广者,以盈补虚,为直田也;亦可以半正从以乘广。 “以盈补虚”就是用多余部分填补不足部分,这就是我国传统的“出入相补”法。 “以盈补虚”变圭田为与之等积的直田,即把等腰三角形转化为长方形。刘徽给出两个方法:一种是腰不变,另一种是把腰两等分。