首页理论教育数学史上第一个完整叙述的三角形内角之和定理

数学史上第一个完整叙述的三角形内角之和定理

2023-11-23 理论教育版权反馈

【摘要】：可能在此基础上,毕达哥拉斯第一个证得“任意三角形的三个内角之和为两个直角”。依据命题29,欧几里得推出不少结论,三角形内角和定理就是其中之一。命题32 在任意三角形中,若延长一边,则外角等于二内对角之和,且三角形的三个内角之和等于两直角。此为数学史上第一个完整叙述的三角形内角之和定理,并给出了严密证明。

有史记载的第一位数学家泰勒斯证得“半圆上的圆周角是直角”。可能在此基础上,毕达哥拉斯第一个证得“任意三角形的三个内角之和为两个直角”。这在当时应是一个了不起的研究成果。不管三角形大还是小,是等腰三角形还是斜三角形,即不管什么形状的三角形,这个结论都是对的。

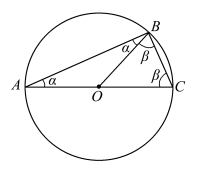
pagenumber_ebook=218,pagenumber_book=209

图3.11.3　泰勒斯定理

pagenumber_ebook=218,pagenumber_book=209

图3.11.4　三角形内角和定理

在毕达哥拉斯200 余年后,古希腊时期乃至整个人类历史上最重要的数学著作《几何原本》问世了。虽然《几何原本》的许多命题可追溯到毕达哥拉斯时代,但欧几里得以公理化形式系统证明了所有命题,实属了不起的杰作。关于三角形的内角和定理,他在第一卷给出4 个相关命题。

命题16 在任意三角形中,若任意延长一边,则其外角大于任何一个内对角。

在证明过程中,欧几里得把线段延长到任意长度,该做法没有任何公设和命题的支持,因而感到其证明有些蹊跷。而命题17 是命题16 的直接推论。(www.chuimin.cn)

命题17 在任意三角形中,任意两角之和小于两直角。

在论证有关三角形的若干性质后,欧几里得从命题27开始讨论平行线相关概念和性质。

命题29 一直线与两条平行线相交,则所成的内错角相等,同位角相等,同旁内角之和等于两直角和。

依据命题29,欧几里得推出不少结论,三角形内角和定理就是其中之一。

命题32 在任意三角形中,若延长一边,则外角等于二内对角之和,且三角形的三个内角之和等于两直角。

此为数学史上第一个完整叙述的三角形内角之和定理,并给出了严密证明。

值得一提的是,历史车轮又向前转了近两千年后,法国“数学神童”帕斯卡来到了世界。他从小就喜欢数学,在父亲精心教育下,12 岁就已精通了欧几里得几何学,且独立发现了一些几何定理,“三角形内角和定理”就是其中之一。